Μια οριζόντια κυκλική πλατφόρμα
μάζας Μ=20kg και ακτίνας R=2m, στρέφεται γύρω από κατακόρυφο άξονα z, χωρίς
τριβές, ο οποίος περνά από το κέντρο της Ο με σταθερή γωνιακή ταχύτητα
ω=2rad/s. Πάνω στην πλατφόρμα είναι τοποθετημένη μια μικρή σφαίρα (αμελητέων
διαστάσεων) και μάζας m=2kg, η οποία είναι δεμένη στο ένα άκρο ιδανικού ελατηρίου σταθεράς
k=100Ν/m και φυσικού μήκους l0=92cm, το άλλο άκρο του οποίου δένεται
στον άξονα περιστροφής. Μεταξύ σφαίρας και πλατφόρμας δεν αναπτύσσονται τριβές,
ενώ η σφαίρα στρέφεται μαζί με την πλατφόρμα, χωρίς να μεταβάλλεται η θέση της
ως προς αυτήν.
i) Το μήκος του ελατηρίου είναι:
α) ℓ < ℓ0, β) ℓ = ℓ0, γ) ℓ > ℓ0.
Να δικαιολογήσετε την απάντησή σας.
ii) Να υπολογιστεί η στροφορμή κάθε σώματος
(πλατφόρμα-σφαίρα), καθώς και η στροφορμή του συστήματος κατά (ως προς) τον
άξονα z.
Σε μια στιγμή t0=0,
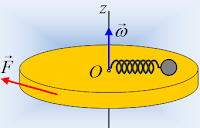
ασκείται εφαπτομενικά στην πλατφόρμα μια οριζόντια, σταθερού μέτρου δύναμη F=10Ν,
όπως στο παραπάνω σχήμα.
iii) Να βρεθούν οι ρυθμοί μεταβολής της στροφορμής
κατά (ως προς) τον άξονα z:
α) του συστήματος,
β) της σφαίρας, γ) της
πλατφόρμας.
iv) Να υπολογιστεί η στροφορμή κάθε σώματος
(πλατφόρμα-σφαίρα), καθώς και η στροφορμή του συστήματος κατά (ως προς) τον
άξονα z, τη στιγμή t1=5s.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.