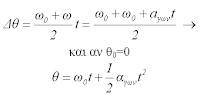Στην ήρεμη επιφάνεια μιας λίμνης επιπλέει ένας ξύλινος δίσκος μάζας Μ=1kg και ακτίνας R=1m.
Ο δίσκος, εξ αιτίας ενός ανεμοστρόβιλου που προηγήθηκε, περιστρέφεται γύρω από κατακόρυφο άξονα που περνά από το κέντρο του με κυκλική συχνότητα ω0=6rad/s.
Πάνω στον δίσκο και στα άκρα μιας διαμέτρου του κάθονται, "γαντζωμένα", δυο χελωνάκια μάζας m=0,2kg το κάθε ένα, τα οποία κάποια χρονική στιγμή ξεκινούν προς συνάντησή τους με ταχύτητες ίσου μέτρου.
Αν γνωρίζουμε ότι τα χελωνάκια ζαλίζονται και αποκοιμούνται όταν η κυκλική συχνότητα με την οποία περιστρέφονται γίνει ω=9rad/s:
Α. Να δικαιολογηθεί γιατί:
α. η κυκλική συχνότητα μεγαλώνει καθώς πλησιάζουν τα χελωνάκια
β. τα χελωνάκια θα αποκοιμηθούν.
Β. Να βρεθούν:
α. η απόσταση από το κέντρο του δίσκου στην οποία θα βρεθεί κάθε χελωνάκι τη στιγμή που θα αποκοιμηθεί
β. η ενέργεια που δαπάνησε το κάθε ένα κατά τη μετακίνησή του.
Η ροπή αδράνειας του δίσκου δίδεται από τη σχέση: Ιδ=ΜR2/2.
Οι τριβές που συναντά ο δίσκος κατά την κίνησή του στο νερό θεωρούνται ασήμαντες.
Τα χελωνάκια θεωρούνται υλικά σημεία.
(Για την ιστορία την άσκηση είχα προτείνει, ως μέλος της επιτροπής, στον Πανελλήνιο διαγωνισμό Φυσικής της ΕΕΦ το 2005 και είχε τεθεί ως θέμα με μικρές παραλλaγές)
Απάντηση
Κυριακή 31 Ιανουαρίου 2010
Σύνθετη κίνηση στερεού.
Πάνω σε μια παγωμένη λίμνη ηρεμεί μια ομογενής σανίδα μήκους 4m. Σε μια στιγμή t=0 ένα κινούμενο υλικό σημείο Σ, συγκρούεται με τη σανίδα με αποτέλεσμα, αμέσως μετά την κρούση τα άκρα Α και Β της σανίδας να αποκτήσουν ταχύτητες υΑ=20m/s και υΒ=40m/s αντίστοιχα, όπως στο σχήμα (α).
α) Ποια η ταχύτητα του μέσου Ο της σανίδας.
β) Να βρεθεί η γωνιακή ταχύτητα περιστροφής της σανίδας, γύρω από το κέντρο μάζας της Ο.
γ) Σε πόσο χρόνο για πρώτη φορά η σανίδα θα βρεθεί στη θέση του σχήματος β;
δ) Για τη θέση (β):
i) Ποιο είναι το άκρο Α και ποιο το Β;
ii) Το άκρο Α ή το Β έχει μεγαλύτερη ταχύτητα;
iii) Να βρεθεί η επιτάχυνση του κέντρου Ο και του άκρου Α της σανίδας.
Μετακόμιση μιας ντουλάπας και ισχύς κινητήρα
Η ομογενής ορθογώνια ντουλάπα του σχήματος έχει βάρος Β και λόγο ακμών L/h=3/4. Η ντουλάπα αρχικά ηρεμεί σε οριζόντια θέση όπως φαίνεται στο σχήμα. Πέντε εργάτες μπορούν ίσα-ίσα να σηκώσουν τη ντουλάπα αλλά όχι να την επιταχύνουν προς τα επάνω.
Α
Οι εργάτες θέλουν περιστρέψουν τη ντουλάπα ώστε αυτή να έρθει σε κατακόρυφη θέση, οπότε «σκαλώνουν» την κάτω δεξιά ακμή όπως φαίνεται στο σχήμα.
Α1
Να υποδείξετε το βέλτιστο σημείο εφαρμογής της συνολικής δύναμης καθώς και τον βέλτιστο φορέα δράσεως αυτής
Α2
Να υπολογίσετε πόσοι εργάτες χρειάζονται για την περιστροφή
Α3
Να υπολογίσετε πόσο συνολικά είναι το ελάχιστο απαιτούμενο μηχανικό έργο που ώστε η ντουλάπα να έρθει σε κατακόρυφη θέση
Β
Αφού η ντουλάπα ισορροπήσει σε κατακόρυφη θέση συνδέεται μέσω μη εκτατού ιμάντα με τροχαλία που στρέφεται με τη βοήθεια κινητήρα. Η τροχαλία συνδέεται στον ακλόνητο τοίχο μέσω βραχίονα. Θεωρείστε ότι το βάρος της τροχαλίας και του βραχίονα είναι αμελητέα σε σύγκριση με το βάρος των φορτίων.
Β1
Να υπολογίσετε τη μηχανική ισχύ που προσφέρει ο κινητήρας αν η ντουλάπα ανέρχεται ισοταχώς με ταχύτητα u
Β2
Να υπολογίσετε τη γωνία που πρέπει να σχηματίζει ο βραχίονας με τον τοίχο ώστε να μην υπάρχει ροπή ως προς το σημείο επαφής τους
Σάββατο 30 Ιανουαρίου 2010
ΠΕΡΙΣΤΡΟΦΗ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΕΠΙΒΡΑΔΥΝΟΜΕΝΟΣ ΑΠΟ ΔΥΟ ΑΒΑΡΗΣ ΡΑΒΔΟΥΣ
Κυκλικός δίσκος ακτίνας R και μάζας m, περιστρέφεται με σταθερή γωνιακή ταχύτητα ω0 (η τριβή στον άξονα περιστροφής θεωρείται αμελητέα). Προκειμένου να επιβραδύνουμε το κυκλικό δίσκο, χρησιμοποιούμε αβαρής ράβδους μήκους ℓ, όπου στο άκρο της καθεμίας, τη χρονική στιγμή t=0 ασκείται δύναμη F. Οι δυνάμεις αυτές ασκούνται μέσω δύο όμοιων ελατηρίων, σταθεράς k και φυσικού μήκους ℓ0, όπως φαίνεται στο παρακάτω σχήμα (τα ελατήρια έχουν την ίδια συσπείρωση x).
_2.jpg) Αν ο συντελεστής τριβής μεταξύ ράβδου (ρ1) και κυκλικού δίσκου είναι μ1, ενώ μεταξύ ράβδου (ρ2) και δίσκου είναι μ2, με μ1>μ2, και η κατακόρυφη συνιστώσα της δύναμης που ασκεί η άρθρωση στο άκρο Β της ράβδου (ρ2) είναι Νy, να υπολογιστούν:
Αν ο συντελεστής τριβής μεταξύ ράβδου (ρ1) και κυκλικού δίσκου είναι μ1, ενώ μεταξύ ράβδου (ρ2) και δίσκου είναι μ2, με μ1>μ2, και η κατακόρυφη συνιστώσα της δύναμης που ασκεί η άρθρωση στο άκρο Β της ράβδου (ρ2) είναι Νy, να υπολογιστούν:α) η συσπείρωση x των ελατήριων και οι κάθετες αντιδράσεις που δέχονται οι ράβδοι από τον κυκλικό δίσκο, στα σημεία Κ και Μ. Επίσης να δείξετεΤ1(2d)>Τ2(3Rσυνφ).
β) η γωνιακή επιτάχυνση (επιβράδυνση) του κυκλικού δίσκου.
γ) η χρονική στιγμή, κατά την οποία ο κυκλικός δίσκος σταματάει να κινείται.
δ) ο αριθμός των περιστροφών που εκτελεί ο δίσκος, μέχρι να μηδενιστεί η γωνιακή του ταχύτητα.
ε) το έργο των ροπών των δυνάμεων που επιβραδύνουν το δίσκο, μέχρι να σταματήσει να κινείται.
στ) το πόσο της θερμικής ενέργειας που εκλύεται, όταν ο δίσκος έχει εκτελέσει n1 περιστροφές.
ζ) ο ρυθμός μεταβολής της κινητικής ενέργειας του δίσκου, κατά τη χρονική στιγμή που ω=ω0/4.
η) ο ρυθμός μεταβολής της στροφορμής του δίσκου.
θ) η συνολική στιγμιαία ισχύς των ροπών των δυνάμεων που επιβραδύνουν το κυκλικό δίσκο, τη χρονική στιγμή κατά την οποία γίνεται ω=ω0/3.
ι) η μέση συνολική ισχύς των ροπών των δυνάμεων που επιβραδύνουν το κυκλικό δίσκο.
κ) το ρυθμό με τον οποίο πρέπει να προσφέρουμε ενέργεια στο δίσκο, ώστε η ταχύτητα του να παραμένει αμετάβλητη.
Δίνεται Ιc=(1/2)mR^2, α= d/3
Στρίψιμο Νομίσματος
Στρίβουμε ένα νόμισμα μάζας m και ακτίνας R στον αέρα. Τη στιγμή t=0 που το νόμισμα εγκαταλείπει το χέρι μας κινούμενο κατακόρυφα προς τα πάνω είναι οριζόντιο, το ένα άκρο Α μιας διαμέτρου του ΑΓ έχει μηδενική ταχύτητα και στρέφεται γύρω από οριζόντιο άξονα κάθετο στην ΑΓ που διέρχεται από το κέντρο μάζας του.
Αν το κέντρο μάζας του νομίσματος κινηθεί κατακόρυφα προς τα πάνω και φθάσει σε ύψος h, να βρείτε:
α. Τη ταχύτητα του σημείου Γ τη στιγμή t=0 και τον αριθμό των στροφών που θα εκτελέσει το νόμισμα μέχρι τη στιγμή που το κέντρο μάζας του νομίσματος θα ξαναπεράσει από το σημείο εκτόξευσης.
β. Την ενέργεια που καταναλώσαμε γι’ αυτή τη ρίψη.
Δίνονται: η ροπή αδρανείας νομίσματος ως προς τον άξονα περιστροφής του, I=(1/4)mR^2 και τα m, g, R, h.
Η αντίσταση του αέρα παραλείπεται.
(Θέμα Πανελ. Διαγ. Φυσικής 2003)
Πρόσθετο ερώτημα
Αν η ρίψη του νομίσματος γίνεται με απότομο (δηλ. πολύ μικρής χρονικής διάρκειας) κατακόρυφο χτύπημα προς τα πάνω, σε σημείο Λ της διαμέτρου ΑΓ, να βρεθεί η απόσταση του σημείου Λ από το κέντρο Κ του νομίσματος.
Το βάρος του νομίσματος κατά τη πολύ μικρή χρονική διάρκεια του χτυπήματος να θεωρηθεί αμελητέο.
Απάντηση:
ή
εδώ.
Αν το κέντρο μάζας του νομίσματος κινηθεί κατακόρυφα προς τα πάνω και φθάσει σε ύψος h, να βρείτε:
α. Τη ταχύτητα του σημείου Γ τη στιγμή t=0 και τον αριθμό των στροφών που θα εκτελέσει το νόμισμα μέχρι τη στιγμή που το κέντρο μάζας του νομίσματος θα ξαναπεράσει από το σημείο εκτόξευσης.
β. Την ενέργεια που καταναλώσαμε γι’ αυτή τη ρίψη.
Δίνονται: η ροπή αδρανείας νομίσματος ως προς τον άξονα περιστροφής του, I=(1/4)mR^2 και τα m, g, R, h.
Η αντίσταση του αέρα παραλείπεται.
(Θέμα Πανελ. Διαγ. Φυσικής 2003)
Πρόσθετο ερώτημα
Αν η ρίψη του νομίσματος γίνεται με απότομο (δηλ. πολύ μικρής χρονικής διάρκειας) κατακόρυφο χτύπημα προς τα πάνω, σε σημείο Λ της διαμέτρου ΑΓ, να βρεθεί η απόσταση του σημείου Λ από το κέντρο Κ του νομίσματος.
Το βάρος του νομίσματος κατά τη πολύ μικρή χρονική διάρκεια του χτυπήματος να θεωρηθεί αμελητέο.
Απάντηση:
ή
εδώ.
Παρασκευή 29 Ιανουαρίου 2010
Διασύνδεση τροχαλιών

Μια μικρή ομογενής τροχαλία ακτίνας r = 0, 1 m και μια μεγάλη ακτίνας R = 0,2 m, ενώνονται έτσι ώστε να συμπίπτουν τα κέντρα τους, και προκύπτει η διπλή τροχαλία κέντρου Ο2 του σχήματος.
Η τροχαλία αυτή, μπορεί να περιστρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδό της. Στο αυλάκι της μικρής τροχαλίας, είναι τυλιγμένο αβαρές μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου είναι δεμένο σώμα Σ μάζας m = 4 kg.
Στο αυλάκι της μεγάλης τροχαλίας, είναι τυλιγμένο αβαρές μη εκτατό νήμα, το οποίο είναι τυλιγμένο και στο αυλάκι μιας ακόμη τροχαλίας Τ , ακτίνας r = 0,1 m, που μπορεί να περιστρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα που περνά από το κέντρο της Ο1 και είναι κάθετος στο επίπεδό της.
Αρχικά, το σύστημα συγκρατείται σε ηρεμία με τα κατακόρυφα νήματα τεντωμένα, και τη χρονική στιγμή t = 0 αφήνεται ελεύθερο.
Η ροπή αδράνειας της διπλής τροχαλίας ως προς τον άξονα που περιστρέφεται είναι Ι2 = 0,08 kgm² και της τροχαλίας Τ είναι Ι1 = 0,02 kgm².
Να υπολογίσετε:
1. Την επιτάχυνση του σώματος Σ.
2. Τις γωνιακές ταχύτητες με τις οποίες στρέφονται οι τροχαλίες τη χρονική στιγμή t1 = 6 s.
3. Το κλάσμα της αρχικής δυναμικής ενέργειας του σώματος Σ που έχει μεταβιβαστεί σε κάθε τροχαλία μέχρι την παραπάνω χρονική στιγμή.
4. Τους ρυθμούς των ενεργειακών μεταβολών που παρατηρούνται στην τροχαλία Τ , στη διπλή τροχαλία και στο σώμα Σ την χρονική στιγμή t1.
Δίνεται g = 10 m/s² και ότι, τα νήματα δεν ολισθαίνουν στα αυλάκια των τροχαλιών.
Η τροχαλία αυτή, μπορεί να περιστρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδό της. Στο αυλάκι της μικρής τροχαλίας, είναι τυλιγμένο αβαρές μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου είναι δεμένο σώμα Σ μάζας m = 4 kg.
Στο αυλάκι της μεγάλης τροχαλίας, είναι τυλιγμένο αβαρές μη εκτατό νήμα, το οποίο είναι τυλιγμένο και στο αυλάκι μιας ακόμη τροχαλίας Τ , ακτίνας r = 0,1 m, που μπορεί να περιστρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα που περνά από το κέντρο της Ο1 και είναι κάθετος στο επίπεδό της.
Αρχικά, το σύστημα συγκρατείται σε ηρεμία με τα κατακόρυφα νήματα τεντωμένα, και τη χρονική στιγμή t = 0 αφήνεται ελεύθερο.
Η ροπή αδράνειας της διπλής τροχαλίας ως προς τον άξονα που περιστρέφεται είναι Ι2 = 0,08 kgm² και της τροχαλίας Τ είναι Ι1 = 0,02 kgm².
Να υπολογίσετε:
1. Την επιτάχυνση του σώματος Σ.
2. Τις γωνιακές ταχύτητες με τις οποίες στρέφονται οι τροχαλίες τη χρονική στιγμή t1 = 6 s.
3. Το κλάσμα της αρχικής δυναμικής ενέργειας του σώματος Σ που έχει μεταβιβαστεί σε κάθε τροχαλία μέχρι την παραπάνω χρονική στιγμή.
4. Τους ρυθμούς των ενεργειακών μεταβολών που παρατηρούνται στην τροχαλία Τ , στη διπλή τροχαλία και στο σώμα Σ την χρονική στιγμή t1.
Δίνεται g = 10 m/s² και ότι, τα νήματα δεν ολισθαίνουν στα αυλάκια των τροχαλιών.
Μια σύνθετη κίνηση ενός μολυβιού.
Διαθέτουμε ένα μολύβι μήκους 20cm, το οποίο κρατάμε στο χέρι μας σε οριζόντιο θέση. Σε μια στιγμή εκτοξεύουμε κατακόρυφα το μολύβι, το οποίο ξαναπιάνουμε μετά από 0,4s, στην ίδια θέση, με τον ίδιο προσανατολισμό, ενώ στο μεταξύ το μολύβι έχει κάνει δύο περιστροφές στον αέρα.
Να βρεθούν οι ταχύτητες των δύο άκρων του μολυβιού, τη στιγμή που εγκαταλείπει το χέρι μας. Θεωρείστε ότι το κέντρο μάζας του μολυβιού είναι στο μέσον του Ο και g=10m/s2.
Πέμπτη 28 Ιανουαρίου 2010
Πλαστική κρούση δύο ράβδων
Δύο λεπτοί ράβδοι από σίδηρο έχουν μήκος L1=1,2m και L2=4L1 αφήνονται από οριζόντια θέση και φτάνουν ταυτόχρονα στην κατακόρυφη θέση τους όπως φαίνεται στο παρακάτω σχήμα.
Οι δύο ράβδοι έχουν κοινό οριζόντιο άξονα περιστροφής το ανώτερο σημείο της κάθε ράβδου. Η μάζα της μικρής ράβδου είναι m1=1kg.Την στιγμή της κρούσης των δύο ράβδων μέσω μιας ασφάλειας οι δύο ράβδοι κλειδώνουν μεταξύ τους έτσι ώστε το σύστημα να συμπεριφέρεται πλέον σαν μία ράβδος. Να βρεθούν:
A) Oι μέγιστες γωνιακές ταχύτητες των δύο ράβδων πριν την πλαστική τους κρούση
Β) Η ροπή αδράνειας του συστήματος των δύο ράβδων μετά την πλαστική τους κρούση
Γ) Το συνημίτονο της μέγιστης γωνίας σε σχέση με την κατακόρυφη που θα διαγράψει το σύστημα των δύο ράβδων μετά την πλαστική τους κρούση.
Δίνεται για την κάθε ράβδο Ιο=1/3Μ.L2.
Τετάρτη 27 Ιανουαρίου 2010
Μια κρούση με Doppler
Πάνω σε ένα λείο κεκλιμένο γωνίας κλίσης φ=30ο και στην βάση του κεκλιμένου επιπέδου βρίσκεται σώμα μάζας M1 που συνδέεται με ελατήριο σταθεράς Κ=100N/m. Στο άλλο άκρο του ελατηρίου είναι δεμένο δεύτερο σώμα μάζας Μ2= 1Kg όπως στο σχήμα.
Ένα τρίτο σώμα κινείται οριζόντια με ταχύτητα U=√3m/sec έχει μάζα M3=2 Κg σφηνώνεται στο σώμα μάζα Μ2.Το σώμα μάζας Μ1 έχει ενσωματωμένη πάνω του μία πηγή παραγωγής ήχων με συχνότητα Fs=680Hz.Μετά την πλαστική κρούση των δύο σωμάτων το σώμα Μ1 μόλις και δεν χάνει την επαφή του με το κάθετο τμήμα της βάσης του κεκλιμένου επιπέδου. Να βρεθούν :
A) To πλάτος ταλάντωσης που θα εκτελέσει το συσσωμάτωμα
B) Η μάζα Μ1
Γ) Η εξίσωση της συχνότητας που καταγράφει ένας ανιχνευτής ήχων που βρίσκεται στο σώμα Μ2 που δεν καταστρέφεται από την πλαστική κρούση.
Δ) Η γραφική παράσταση της συχνότητας με το χρόνο
Δίνεται το Uηχ=340m/sec.
Ένα μηχανικό σύστημα μετά από έκρηξη.
Σώμα μάζας ΜΑ1=6Κg είναι δεμένο σε oριζόντιο ελατήριο σταθεράς Κ=100Ν/m.To άλλο άκρο του ελατηρίου είναι δεμένο σε δεύτερο σώμα μάζας ΜΑ2=2Κg.To όλο σύστημα ισορροπεί πάνω σε λείο οριζόντιο επίπεδο μεγάλου μήκους. Ξαφνικά και εξαιτίας μιας έκρηξης το σώμα ΜΑ1 σπάει σε δύο κομμάτια που το ένα έχει διπλάσια μάζα από το άλλο. Από αυτά το μικρότερο κομμάτι μένει δεμένο στο ελατήριο και κινείται οριζόντια έτσι ώστε να αρχίζει να συσπειρώνει το ελατήριο. Αν η ενέργεια της έκρηξης που μεταφέρθηκε στα κομμάτια του ΜΑ1 ήταν 6 J να βρεθούν:
Α) Τα μέτρα των ταχυτήτων των κομματιών του ΜΑ1 μετά την έκρηξη
Β) Η μέγιστη συσπείρωση του ελατηρίου
Γ) Τα μέτρα των ταχυτήτων των σωμάτων όταν το ελατήριο αποκτήσει για πρώτη φορά μετά την έκρηξη το φυσικό του μήκος.
Διαγώνισμα στα κύματα. Διάρκεια 1,5h.
1) Κατά μήκος γραμμικού ελαστικού μέσου, διαδίδεται ένα εγκάρσιο αρμονικό κύμα, χωρίς απώλειες ενέργειας.
i) Τα μόρια του μέσου ταλαντώνονται στη διεύθυνση διάδοσης του κύματος.
ii) Σχηματίζονται «όρη» και «κοιλάδες».
iii) Η μέγιστη ταχύτητα ταλάντωσης των μορίων δίνεται από την εξίσωση υmαx =λf.
iv) Η ταχύτητα διάδοσης του κύματος δίνεται από την εξίσωση υ=ωKΑ.
Μονάδες 10
2) Χαρακτηρίστε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες
i) Το μήκος κύματος ενός αρμονικού κύματος είναι σταθερό και ανεξάρτητο του μέσου διάδοσης του κύματος
ii) Τα Η/Μ κύματα δημιουργούνται όταν κινούνται ηλεκτρικά φορτία.
iii) Στην επιφάνεια ενός υγρού διαδίδονται δύο κύματα με μήκος κύματος λ=2cm, από σύγχρονες πηγές οι οποίες ταλαντώνεται με εξισώσεις y=A∙ημωt. Ένα σημείο Σ απέχει 7cm από την πρώτη και 15cm από τη δεύτερη πηγή και μετά τη συμβολή των δύο κυμάτων, ταλαντώνεται με πλάτος 0,6 cm.i) Θεωρούμε ότι τα κύματα διαδίδονται με σταθερό πλάτος.
α) Κάθε πηγή ταλαντώνεται με πλάτος 0,3cm
α) Κάθε πηγή ταλαντώνεται με πλάτος 0,3cm
β) Ένα άλλο σημείο Ρ που ισαπέχει από τις δύο πηγές ταλαντώνεται με πλάτος 0,3m
γ) Η απόσταση των δύο πηγών μπορεί είναι μεγαλύτερη από 25cm.
Μονάδες 10
3) Κατά μήκος γραμμικού ομογενούς ελαστικού μέσου, το οποίο έχει τη διεύθυνση του άξονα x'x, διαδίδεται εγκάρσιο αρμονικό κύμα, μήκους κύματος λ = 20 cm, προς τη αρνητική κατεύθυνση του άξονα. Η απομάκρυνση ενός σημείου Ο, το οποίο θεωρούμε ως αρχή του άξονα, δίνεται από την εξίσωση:
y = 3ημ20πt (y σε cm, t σε s).
Με ποιο ή ποια από τα παρακάτω συμφωνείτε ή διαφωνείτε και γιατί;
i) Η εξίσωση του κύματος είναι y = 3ημπ (10t + x/10) (χ, y σε cm, t σε s).
ii) Η διαφορά φάσης φΑ - φΒ μεταξύ των ταλαντώσεων δύο σημείων Α (20 cm) και Β (- 40 cm), την ίδια χρονική στιγμή, είναι 6π.
iii) Η ταχύτητα διάδοσης του κύματος είναι υ = 2 m/s.
Μονάδες 12
4) Πάνω σε μια χορδή έχει σχηματιστεί ένα στάσιμο κύμα με εξίσωση:
y= 0,2 συν2πx∙ημ2πt (μονάδες στο S.Ι.)
Να βρείτε τις θέσεις των δεσμών και να αποδείξτε ότι η απόσταση μεταξύ δύο διαδοχικών δεσμών είναι ίση με ½ m.
Μονάδες 8
5) Μια μονοχρωματική ακτίνα προσπίπτει όπως στο σχήμα στο πλακίδιο Α. Στο σχήμα φαίνεται η πορεία της, μέχρι της έξοδό της ξανά στον αέρα.
i) Σημειώστε στο σχήμα τις γωνίες πρόσπτωσης και διάθλασης στο σημείο Γ.
ii) Σε ποιο πλακίδιο, στο Α ή στο Β η ακτίνα έχει μεγαλύτερη ταχύτητα διάδοσης; Να δικαιολογήσετε την απάντησή σας.
Αν η γωνία διάθλασης στο Γ είναι 30° και ο δείκτης διάθλασης n2=1,2, τότε o δείκτης διάθλασης n1 είναι:
Να δικαιολογήσετε την επιλογή σας
Μονάδες 3+3+4=10
6) Έστω δυο σημεία Β και Γ πάνω σε ένα γραμμικό ελαστικό μέσο, (ας θεωρήσουμε του άξονα x΄x) κατά μήκος του οποίου διαδίδεται ένα εγκάρσιο αρμονικό κύμα της μορφής:
y =Αημ2π(t/T – x/λ)
Η απόσταση ΒΓ είναι ίση με d = 5λ/4, και το κύμα διαδίδεται από το Β προς το Γ.
Κάποια χρονική στιγμή t0 το κύμα φτάνει στο σημείο Γ, ενώ το σημείο Β βρίσκεται στη μέγιστη θετική απομάκρυνσή του.
i) Να σχεδιάσετε τμήμα του στιγμιότυπου του κύματος από το Β μέχρι το Γ τη χρονική στιγμή t0.
ii) Η εξίσωση ταλάντωσης του σημείου Β είναι:
yΒ = 0,1ημ(5πt -π) SI.
Να βρεθεί το πλάτος, η συχνότητα του κύματος, όπως επίσης και το χρονικό διάστημα που απαιτείται για να διαδοθεί το κύμα από το Β στο Γ.
iii) Να βρείτε την εξίσωση της απομάκρυνσης – χρόνου για το σημείο Γ.
iv) Αν τη χρονική στιγμή t1=t0+0,1s το κύμα έχει φτάσει σε ένα σημείο Δ το οποίο απέχει κατά 1m από το Γ (στη διεύθυνση του άξονα) να βρείτε την εξίσωση του κύματος και να κάνετε το στιγμιότυπο του κύματος τη στιγμή t1 κατά μήκος του θετικού ημιάξονα x.
Μονάδες 10+(2+3+5)+15+(10+5)=50
Τρίτη 26 Ιανουαρίου 2010
ΣΤΕΡΕΟ - ΑΝΤΙΜΕΤΩΠΙΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΑΛΛΑΓΗΣ ΣΤΡΟΦΙΚΗΣ ΚΑΤΑΣΤΑΣΗΣ - ΤΥΠΟΙ
Σ' ένα πρόβλημα, παρατηρώ αλλαγή στη στροφική κατάσταση ενός στερεού (ή συστήματος στερεών), καθώς αυτό δέχεται εξωτερικές ροπές. Θα έχω στο νου μου τρείς (3) τρόπους για να τ' αντιμετωπίσω :
1. Τη "δυναμική προσέγγιση" και τους τύπους της Ομαλά Μεταβαλλόμενης Μεταφορικής και Στροφικής Κίνησης.
2. Την "Αρχή Διατήρησης της Μηχανικής Ενέργειας" (Α.Δ.Μ.Ε).
3. Το "Θεώρημα Έργου - Ενέργειας" (Θ.Ε-Ε).
Αναλυτικά …
1. Τη "δυναμική προσέγγιση" και τους τύπους της Ομαλά Μεταβαλλόμενης Μεταφορικής και Στροφικής Κίνησης.
2. Την "Αρχή Διατήρησης της Μηχανικής Ενέργειας" (Α.Δ.Μ.Ε).
3. Το "Θεώρημα Έργου - Ενέργειας" (Θ.Ε-Ε).
Αναλυτικά …
Κυκλική κίνηση.
Λίγη εισαγωγική θεωρία πάνω στην κυκλική κίνηση, την οποία είχα αναρτήσει παλιότερα και την οποία επαναφέρω για τους νέους φίλους που ήρθαν στο μεταξύ στην συντροφιά μας.
Τι πρέπει να ξέρει ένας μαθητής πριν αρχίσει να διδάσκεται την Μηχανική στερεού, από την κυκλική κίνηση υλικού σημείου, την οποία διδάχτηκε ή θα έπρεπε να διδαχτεί στην Α΄Λυκείου.
Ένα υλικό σημείο εκτελεί κυκλική κίνηση σε οριζόντιο επίπεδο, με ακτίνα R γύρω από το σημείο Ο, όπως στο σχήμα.
Πώς μπορούμε να μελετήσουμε την κίνηση του υλικού σημείου; Με δύο διαφορετικούς τρόπους:
1) Με χρήση γραμμικών μεγεθών.
Ποια είναι αυτά; Το μήκος του τόξου που διαγράφει σε κάποιο χρονικό διάστημα, o ρυθμός μεταβολής του μήκους του τόξου αυτού, που είναι η ταχύτητα του υλικού σημείου, και ο ρυθμός μεταβολής της ταχύτητάς του, δηλαδή η επιτάχυνσή του.
Αναφερόμενοι λοιπόν στο παραπάνω σχήμα, αν το σώμα σε χρόνο dt μετακινείται από τη θέση Α στην Β διαγράφοντας το τόξο ds, ορίζουμε την ταχύτητά του (που από εδώ και πέρα θα ονομάζουμε γραμμική ταχύτητα) από την σχέση:
Η γραμμική ταχύτητα είναι πάνω στο επίπεδο της κυκλικής τροχιάς, εφαπτόμενη στον κύκλο (πράγμα που σημαίνει κάθετη στην ακτίνα σε κάθε σημείο).
Η ταχύτητα του υλικού σημείου σε μια κυκλική κίνηση μεταβάλλεται ΠΑΝΤΑ. Ακόμη και αν το μέτρο της παραμένει σταθερό θα αλλάζει η κατεύθυνσή της, αφού θα είναι πάντα εφαπτόμενη του κύκλου. Συνεπώς πάντα υπάρχει επιτάχυνση. Ορίζεται από την γνωστή σχέση:
Ενώ η κατεύθυνσή της είναι προς το εσωτερικό μέρος της κυκλικής τροχιάς. Η επιτάχυνση αυτη μεταβάλλει και το μέτρο και την κατεύθυνση της ταχύτητας. Μπορούμε λοιπόν να αναλύσουμε την επιτάχυνση αυτή σε δύο συνιστώσες. Μια στη διεύθυνση της ταχύτητας, η οποία θα μεταβάλλει το μέτρο της ταχύτητας και μια κάθετη στην ταχύτητα με φορά προς το κέντρο του κύκλου, η οποία μεταβάλλει την κατεύθυνση της ταχύτητας.
Η συνιστώσα αε που είναι κάθετη στην ακτίνα ονομάζεται επιτρόχια επιτάχυνση και αν έχει την ίδια κατεύθυνση με την ταχύτητα θα είναι υπεύθυνη για την αύξηση του μέτρου της ταχύτητας (επιταχυνόμενη κίνηση), ενώ αν έχει αντίθετη φορά, θα μειώνει το μέτρο της ταχύτητας (επιβραδυνόμενη κίνηση).
Η συνιστώσα ακ ονομάζεται κεντρομόλος επιτάχυνση το μέτρο της οποίας δίνεται από την εξίσωση:
Να τονίσουμε ότι αυτή ευθύνεται για την αλλαγή στην κατεύθυνση της ταχύτητας, είναι αυτή που κρατά το σώμα σε κυκλική τροχιά.
Είναι προφανές ότι για έχει το σώμα επιτάχυνση, θα πρέπει να δέχεται και αντίστοιχη συνισταμένη δύναμη, σύμφωνα με τον δεύτερο νόμου του Νεύτωνα. Δηλαδή η συνισταμένη θα έχει την κατεύθυνση της επιτάχυνσης και συνεπώς και αυτή θα μπορούσαμε να την αναλύσουμε επίσης σε δύο συνιστώσες, μια εφαπτομενική ΣFε=m·αε και μια προς το κέντρο του κύκλου, την οποία λέμε και κεντρομόλο δύναμη, ΣFR=m·ακ.
2) Με χρήση γωνιακών μεγεθών.
Αν το υλικό μας σημείο μετακινείται από την θέση (Α) στη θέση (Β), η επιβατική ακτίνα (η ακτίνα που δίνει κάθε στιγμή τη θέση του κινητού) διαγράφει την επίκεντρη γωνία dθ. Γνωρίζοντας λοιπόν τη γωνία που διαγράφει το κινητό γνωρίζουμε κάθε στιγμή και την θέση του.
Μπορούμε και εδώ να ορίσουμε τον ρυθμό με τον οποίο μεταβάλλεται η παραπάνω γωνία. Το μέγεθος που προκύπτει ονομάζεται Γωνιακή ταχύτητα. Αυτή είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο κέντρο του κύκλου, με φορά που καθορίζεται από τον κανόνα του δεξιού χεριού, όπως στο σχήμα:
Και το μέτρο της οποίας θα είναι:
με μονάδα μέτρησης το 1 rad/s.
Αν μεταβάλλεται η γωνιακή ταχύτητα, τότε ορίζουμε το ρυθμό μεταβολής της, τον οποίο ονομάζουμε γωνιακή επιτάχυνση:
Η γωνιακή επιτάχυνση είναι επίσης κάθετη στο επίπεδο της κυκλικής τροχιάς στο κέντρο του κύκλου, ενώ η φορά της μπορεί να είναι ίδια με την φορά της γωνιακής ταχύτητας (σχ.1) ή αντίθετης φοράς (σχ.2). Στην πρώτη περίπτωση η γωνιακή ταχύτητα του σώματος αυξάνεται (επιταχυνόμενη κίνηση) ενώ στην δεύτερη μειώνεται (επιβραδυνόμενη κίνηση).
3) Πώς συνδέονται τα παραπάνω μεγέθη;
Η επίκεντρη γωνία dθ και το αντίστοιχο μήκος του τόξου στο οποίο βαίνει συνδέονται με την σχέση:
Παρατηρείστε ότι η γωνία είναι αδιάστατο μέγεθος, συνεπώς δεν έχει μονάδες. Καταχρηστικά και για λόγους διευκόλυνσης μετράμε τις γωνίες σε rad, όπου όταν μια επίκεντρη γωνία βαίνει σε τόξο με μήκος ίσο με την ακτίνα του κύκλου, λέμε ότι είναι ίση με 1 ακτίνιο (rad).
Από την (1) και δουλεύοντας με μέτρα παίρνουμε:
Προσέξτε ότι η σχέση (2) συνδέει τα μέτρα της γραμμικής και γωνιακής ταχύτητας. Μην ξεχνάμε ότι τα διανύσματα είναι όπως λέμε ασύμβατα κάθετα. Το ένα οριζόντιο το άλλο κατακόρυφο, χωρίς να περνάνε από το ίδιο σημείο.
Παραγωγίζοντας την εξίσωση (2) παίρνουμε:
Βλέπουμε ότι το dυ/dt είναι ο ρυθμός μεταβολής του μέτρου της γραμμικής ταχύτητας που συνδέεται με την επιτρόχια επιτάχυνση. Προσοχή λοιπόν και η σχέση (3) συνδέει επίσης τα μέτρα της επιτρόχιας και της γωνικής επιτάχυνσης.
4) Δύο εύκολες κυκλικές κινήσεις.
Α) Ομαλή κυκλική κίνηση:
Αν το υλικό μας σημείο στρέφεται με ταχύτητα σταθερού μέτρου, τότε η κίνηση ονομάζεται ομαλή κυκλική κίνηση. Αλλά τότε δεν θα υπάρχει επιτρόχια επιτάχυνση και θα μπορούσαμε να γράψουμε:
Δs= υ·Δt και αν t0=0 και s0=0 θα είχαμε s=υ·t
Ή αναφερόμενοι σε γωνιακά μεγέθη, αφού η γραμμική ταχύτητα έχει σταθερό μέτρο, από την σχέση (2) προκύπτει ότι και το μέτρο της γωνιακής ταχύτητας παραμένει σταθερό, οπότε αντίστοιχα θα έχουμε:
Δθ=ω·Δt και αν t0=0 και θ0=0 θα είχαμε και θ=ωt (σας θυμίζει τίποτα;).
Β) Ομαλά μεταβαλλόμενη κυκλική κίνηση:
Αν ο ρυθμός μεταβολής της γραμμικής ταχύτητας είναι σταθερός, δηλαδή αε=σταθερή και η γωνιακή επιτάχυνση είναι σταθερή, όπως προκύπτει από τη σχέση (3) και η κίνηση θα είναι είτε κυκλική ομαλά επιταχυνόμενη, είτε κυκλική ομαλά επιβραδυνόμενη και τότε:
Για τα γραμμικά μεγέθη θα ισχύουν οι γνωστές μας σχέσει για το μέτρο της ταχύτητας και για το μήκος του διανυόμενου τόξου:
υ= υ0 ± αε·t και Δs = υ0·t ± ½ αε·t2.
Ενώ όσον αφορά τα γωνιακά μεγέθη θα έχουμε:
ω=ω0 ± αγων·Δt και αν t0=0 θα έχουμε:
ω = ω0 ± αγων·t ( 4)
Αν τέλος κάνουμε τη γραφική παράσταση της γωνιακής ταχύτητας σε συνάρτηση με το χρόνο (για την επιταχυνόμενη κίνηση) παίρνουμε το παρακάτω διάγραμμα:
όπου το εμβαδόν του γκριζαρισμένου τραπεζίου είναι αριθμητική ίσο με την γωνία:
Εγγραφή σε:
Αναρτήσεις (Atom)