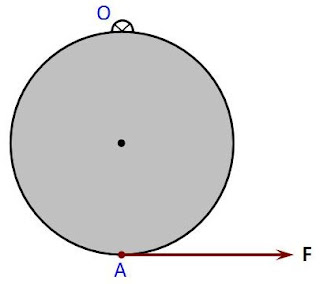
Μια ομογενής ράβδος ΑΓ, στρέφεται με γωνιακή ταχύτητα ω γύρω από κάθετο άξονα που διέρχεται από το ένα της άκρο Α.
Τι κίνηση κάνει; Ποιας μορφής Κινητική ενέργεια έχει;
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι= 1/12 Μl2.
Απάντηση:
1) Η κίνηση μπορεί να θεωρηθεί ότι είναι μόνο ομαλή στροφική γύρω από τον άξονα με αποτέλεσμα να έχει μόνο κινητική ενέργεια λόγω περιστροφής:
2) Η κίνηση μπορεί να θεωρηθεί σύνθετη.
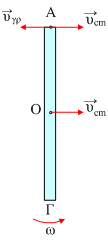
Μια στροφική γύρω από κάθετο άξονα που περνά από το κέντρο μάζας Ο, με γωνιακή ταχύτητα ω και μια μεταφορική του κέντρου μάζας Ο, το οποίο εκτελεί κυκλική κίνηση, σαν υλικό σημείο με γραμμική ταχύτητα:
υγρ=υcm=ω·(ΑΟ) → υcm=ω·l/2
Έτσι για παράδειγμα το άκρο Α έχει μια ταχύτητα λόγω της μεταφορικής κίνησης την υcmκαι μια γραμμική ταχύτητα λόγω της περιστροφικής κίνησης υγρ=ω·R= ω·l/2. Έτσι η ταχύτητα του άκρου Α είναι μηδενική, πράγμα αναμενόμενο αφού από το άκρο αυτό διέρχεται ο σταθερός άξονας περιστροφής.
Αν όμως η κίνηση είναι σύνθετη, τότε θα έχει και μεταφορική και περιστροφικήκινητική ενέργεια.
Άρα
Κολ= Κμετ+Κπερ →
ΣΥΜΠΕΡΑΣΜΑ: Αν ένα στερεό στρέφεται γύρω από σταθερό άξονα, ο οποίος δεν περνά από το κέντρο μάζας, τότε το σώμα έχει και μεταφορική κινητική ενέργεια (Κ= ½ Mυcm2) και περιστροφική κινητική ενέργεια (Kπερ= ½ Ιω2) όπου Ι η ροπή αδράνειας ως προς άξονα που περνά από το κέντρο μάζας του.
Ας έρθουμε τώρα σε μια εφαρμογή των παραπάνω ιδεών:

Η ράβδος του σχήματος εκτελεί μεταφορική κίνηση με ταχύτητα υ0 πάνω σε λείο οριζόντιο επίπεδο. Στο σημείο Ο υπάρχει κατακόρυφος σταθερός άξονας. Όταν το άκρο Α της ράβδου φτάνει στο Ο πιάνεται στον άξονα με τη βοήθεια ενός άγκιστρου με αποτέλεσμα η ράβδος να συνεχίσει με περιστροφική κίνηση.
- Να βρεθεί η γωνιακή ταχύτητα της ράβδου, μετά την σταθεροποίηση του άκρου Α στο άγκιστρο.
- Να υπολογιστεί το έργο της δύναμης (σαν δύναμης) που ασκήθηκε στην ράβδο από το άγκιστρο.
- Να βρεθεί το έργο της ροπής που ασκήθηκε στη ράβδο.
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που περνά από το άκρο της Ι= 1/3 Μl2.