Εσωτερική Ροπή και Εσωτερική Δύναμη

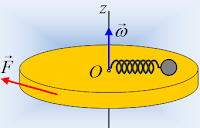
Η ομογενής ράβδος του σχήματος έχει μάζα Μ=0,6 kg και μήκος L=1 m, και στο ένα άκρο της είναι

κολλημένη συμπαγής σφαίρα αμελητέων διαστάσεων με μάζα m=0,2 kg. Το όλο σύστημα μπορεί να στρέφεται ως προς άξονα που διέρχεται από το άλλο άκρο Ο και είναι κάθετο στη σελίδα.

Αρχικά το σύστημα είναι ακίνητο στην οριζόντια θέση και αφήνεται ελεύθερο, οπότε αρχίζει να στρέφεται ως προς άξονα που διέρχεται από το Ο. Να υπολογιστούν:

Α.

α) Να βρεθεί η επιτάχυνση του σώματος m τη στιγμή που το σύστημα αφήνεται ελεύθερο.

β) Η δύναμη που ασκεί η ράβδος στο σώμα m τη στιγμή που το σύστημα αφήνεται ελεύθερο.

Β.

γ) Η δύναμη που ασκεί η ράβδος στο σώμα m τη στιγμή που το σύστημα βρίσκεται στην κατακόρυφη θέση.

δ) Η δύναμη που δέχεται η ράβδος από τον άξονα στην κατακόρυφη θέση.

Γ.

ε) Η γωνιακή ταχύτητα του συστήματος όταν έχει διαγράψει γωνία 60^ο από την αρχική οριζόντια θέση.

στ) Η δύναμη που δέχεται το σφαιρίδιο από τη ράβδο τη στιγμή που το σύστημα έχει διαγράψει γωνία 60^ο από την αρχική οριζόντια θέση.

ζ) Να βρεθεί το έργο της δύναμης F που ασκείται στο m από τη ράβδο κατά τη μετακίνηση του συστήματος από την οριζόντια θέση μέχρι τη στιγμή που διαγράφει γωνία 60^ο από την αρχική θέση.

 συνέχεια εδώ

Η στεφάνη και η σημειακή μάζα.

Μια στεφάνη ακτίνας 0,2m και μάζας m=1kg, η οποία θεωρείται συγκεντρωμένη στην περιφέρειά της, μπορεί να στρέφεται, χωρίς τριβές, σε κατακόρυφο επίπεδο, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από ένα σημείο Ο της περιφέρειάς της. Σε ένα σημείο Α της περιφέρειας της  στεφάνης, όπου η γωνία ΟΚΑ είναι ορθή, έχει προσδεθεί ένα σώμα Σ, ίσης μάζας με τη στεφάνη, το οποίο θεωρείται υλικό σημείο, δημιουργώντας έτσι το στερεό s.  Στρέφουμε το στερεό s, ώστε η ακτίνα της στεφάνης ΚΑ να είναι κατακόρυφη και σε μια στιγμή (t₀=0) το αφήνουμε να περιστραφεί.

i)  Να βρεθεί η ροπή αδράνειας του στερεού s, ως προς τον άξονα περιστροφής στο Ο.

ii) Ποια η αρχική επιτάχυνση του σώματος Σ, μόλις αφήσουμε το στερεό να κινηθεί;

iii) Μετά από λίγο, τη στιγμή t₁, η ακτίνα ΚΑ γίνεται οριζόντια για πρώτη φορά.

Για τη στιγμή αυτή να βρεθούν:

α) Η γωνιακή ταχύτητα του στερεού και η ταχύτητα του σώματος Σ.

β) Η  στροφορμή και ο ρυθμός μεταβολής της στροφορμής του στερεού s,  ως προς τον άξονα περιστροφής του.

γ) Η  στροφορμή και ο ρυθμός μεταβολής της στροφορμής του σώματος Σ,  ως προς το σημείο Ο.

δ) Η κινητική ενέργεια και ο ρυθμός μεταβολής της κινητικής ενέργειας, του στερεού s.

ε) Η κινητική ενέργεια και ο ρυθμός μεταβολής της κινητικής ενέργειας, της στεφάνης.

Δίνεται g=10m/s².

Απάντηση:

ή

	Η  στεφάνη και η σημειακή μάζα.

Ένας περιστρεφόμενος δίσκος αποδεσμεύεται.

Ένας ομογενής δίσκος, μάζας Μ=6kg και ακτίνας R=0,6m μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα, ο οποίος διέρχεται από ένα σημείο Ο της περιφέρειάς του, σε ύψος Η=1,6m από το έδαφος. Φέρνουμε το δίσκο στη θέση του πρώτου σχήματος, ώστε η διάμετρος ΟΒ να είναι οριζόντια και τον αφήνουμε να κινηθεί.

i)  Να υπολογιστεί η αρχική γωνιακή επιτάχυνση του δίσκου, καθώς και η αρχική επιτάχυνση του σημείου Α, στο άκρο της κατακόρυφης διαμέτρου του.

ii) Μετά από λίγο η διάμετρος ΟΒ γίνεται κατακόρυφη, όπως στο δεύτερο σχήμα. Για την θέση αυτή να βρεθούν:

α) Η στροφορμή του δίσκου κατά (ως προς) τον άξονα περιστροφής του.

β) Ο αντίστοιχος ρυθμός μεταβολής της στροφορμής του δίσκου.

γ) η επιτάχυνση του σημείου Α.

iii) Αν τη στιγμή που ο δίσκος βρίσκεται στην παραπάνω θέση, αποδεσμεύεται από τον άξονα περιστροφής του και πέφτει ελεύθερα να υπολογίσετε την κινητική του ενέργεια τη στιγμή που φτάνει στο έδαφος.

Δίνεται η επιτάχυνση της βαρύτητας g=10m/s², ενώ η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι= ½ ΜR².

Απάντηση:

ή

Ένας περιστρεφόμενος δίσκος  αποδεσμεύεται.

Η έννοια «ροπή αδράνειας» στα όρια της Λυκειακής ύλης

Πρόβλημα 1

Μια λεπτή ομογενής ράβδος μήκους ℓ στρέφεται, με σταθερή γωνιακή ταχύτητα ω, γύρω από

κατακόρυφο άξονα έτσι ώστε η ράβδος να σχηματίζει γωνία φ με τον άξονα περιστροφής.

Ο άξονας περιστροφής συνδέεται με το κάτω άκρο της ράβδου με άρθρωση και με το πάνω με αβαρές οριζόντιο νήμα.

Να υπολογιστούν:

α)  Η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της.

β) Η κινητική ενέργεια της ράβδου

γ) Η στροφορμή της ράβδου κατά τον άξονα περιστροφής της.

Πρόβλημα 2: Θεώρημα καθέτων αξόνων

Α) Θεωρούμε ένα επίπεδο στερεό σώμα αμελητέου πάχους και τυχαίου σχήματος. Θεωρούμε τους άξονες x, y, z ανά δύο κάθετους με τους x, y στο επίπεδο του στερεού και τον z να διέρχεται από το σημείο τομής των δύο άλλων και κάθετο στο επίπεδό τους.

Αν Ι_{(x) ,} Ι_(Y), Ι_(z) η ροπή αδράνειας του στερεού ως προς τους άξονες x, y,z αντιστοίχως, να αποδείξετε ότι Ι_(x)  + Ι_(Y),= Ι_(z)  

Β) Ένας λεπτός κυκλικός δακτύλιος μάζας m και ακτίνας R περιστρέφεται με γωνιακή ταχύτητα ω γύρω από μια διάμετρό του. Να βρεθεί η κινητική του ενέργεια.

Η λύση σε word και σε pdf

Το 4ο Θέμα του ΟΕΦΕ 2012 λίγο τροποποιημένο…

Στο σχήμα φαίνεται μια διπλή τροχαλία που αποτελείται από δύο ομόκεντρους ομογενείς δίσκους με ακτίνες r = 0,1m και R = 0,2m και μάζες m = 2kg και Μ=4kg αντίστοιχα. Οι δύο δίσκοι συνδέονται μεταξύ τους έτσι ώστε να περιστρέφονται ως ένα σώμα, χωρίς  τριβές, γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο τους και είναι κάθετος στο επίπεδό τους.

Στο αυλάκι του μεγάλου δίσκου της τροχαλίας έχουμε τυλίξει αβαρές και μη εκτατό νήμα (4), στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα μάζας m₁=1kg. Στο αυλάκι του μικρού δίσκου της τροχαλίας έχουμε τυλίξει δύο αβαρή και μη εκτατά νήματα (3) και (2). Στο ελεύθερο άκρο του οριζόντιου νήματος (3) έχουμε δέσει το ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k₁=200 N/m του οποίου το άλλο άκρο είναι δεμένο σε σταθερό σημείο. Στο ελεύθερο άκρο του κατακόρυφου νήματος (2) έχουμε δέσει σώμα μάζας m₂ =0,5kg το οποίο είναι δεμένο και με αβαρές ελαστικό κατακόρυφο νήμα (1) από σταθερό σημείο της οροφής. Tο μέτρο F της δύναμης που ασκεί το ελαστικό νήμα (1) είναι ανάλογο της επιμήκυνσής του Δℓ σύμφωνα με τη σχέση F=100·Δℓ (SI).

Το σύστημα ισορροπεί με το νήμα (1) να είναι επιμηκυμένο κατά Δℓ = 0,2m.

Δ1. Να βρείτε την παραμόρφωση του ελατηρίου.

Κάποια στιγμή κόβουμε το νήμα (2). Να υπολογίσετε:

Δ2. Τη γωνιακή επιτάχυνση της τροχαλίας αμέσως μετά το κόψιμο του νήματος (2).

Δ3. Να αποδείξετε ότι το σώμα μάζας m₁ εκτελεί ΑΑΤ και να βρείτε τη σταθερά της ταλάντωσής του.

Δ4. Να βρείτε πως μεταβάλλεται η γωνιακή ταχύτητα της τροχαλίας σε συνάρτηση με το χρόνο

Δ5. Τη μέγιστη τιμή της κινητικής ενέργειας του συστήματος (τροχαλία – μάζα m₁).

Δ6. Το διάστημα που θα διανύσει το σώμα μάζας m₂ μέχρι να μηδενιστεί η ταχύτητά του για πρώτη φορά μετά το κόψιμο του νήματος (2).

συνέχεια

Μια κύλιση με μεταβλητή επιτάχυνση.

Γύρω από έναν τροχό, μάζας m=20kg και ακτίνας R=0,6m, ο οποίος βρίσκεται ακίνητος σε οριζόντιο επίπεδο, έχουμε τυλίξει ένα αβαρές νήμα. Σε μια στιγμή t₀=0, ασκούμε στο άκρο του νήματος Α, μια οριζόντια δύναμη F το μέτρο της οποίας μεταβάλλεται με το χρόνο, σύμφωνα με την εξίσωση F=0,9t (μονάδες στο S.Ι.). Ο τροχός αρχίζει να κυλίεται και τη στιγμή t΄=10s σταματάμε να τραβάμε το νήμα και να ασκούμε δύναμη.

i)  Να υπολογίσετε την επιτάχυνση του κέντρου Ο του τροχού σε συνάρτηση με το χρόνο και να κάνετε τη γραφική της παράσταση, μέχρι τη χρονική στιγμή t₂=12s.

ii)  Να υπολογιστεί η στροφορμή του τροχού κατά (ως προς) τον άξονα περιστροφής του τροχού ο οποίος διέρχεται από το κέντρο του Ο, τις χρονικές στιγμές:

   α) t₁=5s  και  β) t₂=12s.

iii) Να υπολογιστεί ο ρυθμός μεταβολής της στροφορμής του τροχού κατά (ως προς) τον άξονα περιστροφής του τροχού ο οποίος διέρχεται από το κέντρο του Ο, τις παραπάνω χρονικές στιγμές.

iv) Πόση ενέργεια μεταφέρθηκε στον τροχό μέσω της ασκούμενης δύναμης F και ποια η ισχύς της δύναμης τη στιγμή t₁;

Δίνεται η ροπή αδράνειας ως προς κάθετο άξονα που περνά από το κέντρο του Ι= ½ mR².

Απάντηση:

ή

	Μια κύλιση με μεταβλητή επιτάχυνση.

Τελικό διαγώνισμα προσομοίωσης Φυσικής 2015-2016

ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ΄ ΤΑΞΗΣ

ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ

24 ΜΑΡΤΙΟΥ 2016

ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ

ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)

 

ΘΕΜΑ  1^ο

Στις ερωτήσεις 1-4  να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.

 

1. Το διπλανό διάγραμμα δείχνει τη χρονική στιγμή t₁ το στιγμιότυπο ενός αρμονικού κύματος το οποίο διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου προς την αρνητική κατεύθυνση. Τι από τα παρακάτω ισχύει;
   α. Τη χρονική στιγμή t₁ το σημείο Α έχει αρνητική ταχύτητα.
   β. Για τις φάσεις των σημείων Α και Β ισχύει φ_Β = φ_Α + π/2.
   γ. Tη χρονική στιγμή t₁ + T/4 το σημείο Β θα είναι ακίνητο.
   δ. Τη χρονική στιγμή t₁ το σημείο Ο έχει αρνητική ταχύτητα.
   (Μονάδες 5)
                        
2. Σε μια εξαναγκασμένη ταλάντωση η περίοδος του διεγέρτη είναι μικρότερη από την ιδιοπερίοδο του ταλαντωτή. Μειώνουμε συνεχώς την περίοδο του διεγέρτη. Το πλάτος της εξαναγκασμένης ταλάντωσης:  
         α. αυξάνεται συνεχώς.
         β. μειώνεται συνεχώς.
         γ. αρχικά μειώνεται και στη συνέχεια αυξάνεται.
         δ. αρχικά αυξάνεται και στη συνέχεια μειώνεται.
   (Μονάδες 5)
    

Σημειακή σφαίρα συγκρούεται πλάγια και ελαστικά με κατακόρυφο τοίχο, έχοντας πριν την κρούση ταχύτητα μέτρου υ που σχηματίζει ...


Η συνέχεια του διαγωνίσματος ΕΔΩ και των απαντήσεων ΕΔΩ


Μια εναλλακτική λυση του Β3 θέματος από τον Κώστα Ψυλλάκο ΕΔΩ. Ευχαριστώ Κώστα.

193.Μερικές θεωρητικές επισημάνσεις στα πειράματα της Γ΄ Λυκείου.

193. Μερικές θεωρητικές επισημάνσεις στα πειράματα της Γ΄ Λυκείου.

Μεγαλύτερες περιπέτειες…

Μετά την ανάρτηση «Ένα σύστημα σωμάτων σε περιπέτειες…» ας πάμε ένα βήμα παρακάτω, στη μελέτη του συστήματος σωμάτων και της εφαρμογής του γενικευμένου νόμου του Νεύτωνα.

--------------------------------------

Μια οριζόντια κυκλική πλατφόρμα μάζας Μ=20kg και ακτίνας R=1m, μπορεί να στρέφεται γύρω από κατακόρυφο άξονα z, χωρίς τριβές, ο οποίος περνά από το κέντρο της Ο. Πάνω στην πλατφόρμα ηρεμεί ένα σώμα Σ μάζας m=2kg, δεμένο στο άκρο νήματος μήκους ℓ=0,8m, το άλλο άκρο του οποίου μέσω ενός δακτυλίου  δένεται στον άξονα z, έτσι ώστε το σώμα Σ μπορεί να περιστρέφεται χωρίς να τυλίγεται το νήμα στον άξονα. Σε μια στιγμή (t₀=0) ασκείται στην περιφέρεια της πλατφόρμας, εφαπτομενικά, μια οριζόντια σταθερού μέτρου δύναμη F=21,6Ν, με αποτέλεσμα τη στιγμή t₁=5s η πλατφόρμα να έχει αποκτήσει γωνιακή ταχύτητα ω₁=10rad/s.

i)  Να εξετάσετε αν υπάρχει τριβή μεταξύ σώματος Σ και πλατφόρμας, με αποτέλεσμα να τεθεί σε περιστροφή και το σώμα Σ.

ii) Να βρεθεί ο ρυθμός μεταβολής της στροφορμής κατά (ως προς) τον άξονα z:

    α) του συστήματος  β)  της πλατφόρμας  και  γ) του σώματος Σ.

στο χρονικό διάστημα 0-5s.

iii) Να υπολογιστεί τη χρονική στιγμή t₁ η στροφορμής κατά (ως προς) τον άξονα z:

     α) του συστήματος  β)  της πλατφόρμας  και  γ) του σώματος Σ.

iv) Τη στιγμή t₁ η δύναμη F καταργείται, οπότε μετά από λίγο παρατηρούμε ότι το σώμα Σ δεν γλιστράει πάνω στην πλατφόρμα. Να υπολογιστεί τότε η ταχύτητα του σώματος Σ.

 Δίνεται η ροπή αδράνειας της πλατφόρμας, ως προς τον άξονά της Ι= ½ ΜR².

Απάντηση:

ή

Μεγαλύτερες περιπέτειες…

192.Ρευστά που ανέβασα στο ylikonet.

192. Ρευστά που ανέβασα στο ylikonet.

191.Υδραντλία.

Ο ηλεκτρικός κινητήρας του σχήματος μάζας m=2,5Kg και ακτίνας r=4cm στρέφεται με γωνιακή ταχύτητα ω₁ και κινεί υδραντλία μάζας Μ=2Κg και ακτίνας R=10cm, η οποία αντλεί 1m³ νερού σε ύψος h=3m μέσα σε 1min. Αν δεν υπάρχουν απώλειες (ιδανική περίπτωση), τότε:

α) Να υπολογιστεί η ωφέλιμη ισχύς της αντλίας.

β) Αν η ροπή που ασκείται από τον ιμάντα στην υδραντλία είναι 5Ν∙m, τότε να υπολογιστεί η σταθερή γωνιακή ταχύτητα ω₁ του κινητήρα.

γ) Πόση είναι η ροπή που ασκείται από τον ιμάντα στον ηλεκτρικό κινητήρα;

Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη της παροχής ηλεκτρικής ενέργειας από το ηλεκτρικό δίκτυο και εξαιτίας των τριβών το σύστημα ακινητοποιείται σε χρόνο Δt. Τότε να βρείτε:

δ) Τη σχέση που συνδέει τις συνολικές ροπές επιβράδυνσης στον κινητήρα και την υδραντλία θεωρώντας ότι αυτές είναι σταθερές.

ε) Το έργο της συνολικής ροπής επιβράδυνσης μέχρι να ακινητοποιηθεί το σύστημα.

Δίνεται για τον ηλεκτρικό κινητήρα και την υδραντλία ότι Ι₁=mr² και Ι₂=MR² αντίστοιχα. Για τις πράξεις θεωρείστε τη πυκνότητα του νερού ρ=10³ Κg∙m³ και g=10m/s².

Συνοπτική λύση:

Ένα σύστημα σωμάτων σε περιπέτειες…

Μια οριζόντια κυκλική πλατφόρμα μάζας Μ=20kg και ακτίνας R=2m, στρέφεται γύρω από κατακόρυφο άξονα z, χωρίς τριβές, ο οποίος περνά από το κέντρο της Ο με σταθερή γωνιακή ταχύτητα ω=2rad/s. Πάνω στην πλατφόρμα είναι τοποθετημένη μια μικρή σφαίρα (αμελητέων διαστάσεων) και μάζας m=2kg, η οποία είναι δεμένη στο ένα άκρο ιδανικού ελατηρίου σταθεράς k=100Ν/m και φυσικού μήκους l₀=92cm, το άλλο άκρο του οποίου δένεται στον άξονα περιστροφής. Μεταξύ σφαίρας και πλατφόρμας δεν αναπτύσσονται τριβές, ενώ η σφαίρα στρέφεται μαζί με την πλατφόρμα, χωρίς να μεταβάλλεται η θέση της ως προς αυτήν.

i) Το μήκος του ελατηρίου είναι:

 α) ℓ < ℓ₀,   β) ℓ = ℓ₀,   γ) ℓ > ℓ₀.

Να δικαιολογήσετε την απάντησή σας.

ii) Να υπολογιστεί η στροφορμή κάθε σώματος (πλατφόρμα-σφαίρα), καθώς και η στροφορμή του συστήματος κατά (ως προς) τον άξονα z.

Σε μια στιγμή t₀=0, ασκείται εφαπτομενικά στην πλατφόρμα μια οριζόντια, σταθερού μέτρου δύναμη F=10Ν, όπως στο παραπάνω σχήμα.

iii) Να βρεθούν οι ρυθμοί μεταβολής της στροφορμής κατά (ως προς) τον άξονα z:

α) του συστήματος,  β) της σφαίρας,   γ) της πλατφόρμας.

iv) Να υπολογιστεί η στροφορμή κάθε σώματος (πλατφόρμα-σφαίρα), καθώς και η στροφορμή του συστήματος κατά (ως προς) τον άξονα z, τη στιγμή t₁=5s.

Απάντηση:

ή

Ένα σύστημα σωμάτων σε περιπέτειες…

Εφαρμογές από τη Φυσική Προσανατολισμού Γ Λυκείου

Εφαρμογές από τη Φυσική  Προσανατολισμού  Γ  Λυκείου

Η επιτάχυνση και ο ρυθμός μεταβολής της στροφορμής.

Ένας οριζόντιος δίσκος μάζας Μ=4m μπορεί να στρέφεται χωρίς τριβές γύρω από τον κατακόρυφο άξονα z, ο οποίος διέρχεται από το κέντρο του Ο. Στην περιφέρεια του δίσκου προσκολλάται ένα αμελητέων διαστάσεων μικρό σώμα Σ, μάζας m, δημιουργώντας έτσι το  στερεό s.

Ασκούμε στο σώμα Σ μια σταθερού μέτρου οριζόντια δύναμη F, με αποτέλεσμα να προκαλέσουμε την περιστροφή του  στερεού.

i) Το σώμα Σ θα αποκτήσει:

α) σταθερού μέτρου επιτάχυνση.

β) επιτάχυνση που θα αυξάνεται καθώς περνά ο χρόνος.

ii) Το σώμα Σ θα αποκτήσει επιτάχυνση στη διεύθυνση της δύναμης F, μέτρου:

α) α=F/m,   β) α=F/2m,   γ) α=F/3m,   δ) α=F/4m,   ε) α=F/5m.

iii) Ο ρυθμός μεταβολής της στροφορμής του σώματος Σ, κατά (ως προς) τον άξονα z:

α) είναι σταθερός,  β) είναι ανάλογος του χρόνου.

iv) Ο ρυθμός μεταβολής της στροφορμής του δίσκου, κατά (ως προς) τον άξονα z, έχει μέτρο:

α) dL/dt= FR/5,     β) dL/dt= 4FR/5,    γ) dL/dt= 2FR/3,    δ) dL/dt= FR.

Να δικαιολογήσετε τις απαντήσεις σας.

Δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονά του Ι= ½ ΜR².

Απάντηση:

ή

Η επιτάχυνση και ο ρυθμός μεταβολής της στροφορμής.