Δύο ράβδοι για μία ταλάντωση.

Στο διπλανό σχήμα βλέπουμε ένα κατακόρυφο ελατήριο σταθεράς k, με το πάνω άκρο του δεμένο στο ταβάνι και το κάτω άκρο του δεμένο στο σφαιρίδιο μάζας m. Το σφαιρίδιο μέσω νήματος συνδέεται με το άκρο συστήματος δύο ράβδων (μάζας Μ η καθεμία) όπου έχουν συγκολληθεί στα άλλα άκρα τους έτσι ώστε η κυρτή γωνία να είναι 120^ο. Στο σχήμα 1, όπως φαίνεται το σύστημα των ράβδων συνδέεται στο άκρο Α με το νήμα, ενώ στο σχήμα 2 συνδέεται στο άκρο Γ. Αν κόψουμε το νήμα στο σχήμα 1, το σφαιρίδιο εκτελεί Α.Α.Τ. πλάτους Α₁ ενώ αν κάνουμε το ίδιο στο σχήμα 2, το σφαιρίδιο εκτελεί ταλάντωση πλάτους Α₂. Για τα δύο πλάτη των ταλαντώσεων ισχύει η σχέση:

α. Α₁ = 2Α₂                                         β. Α₁ = Α₂                                           γ. Α₂ = 2Α₁

Η συνέχεια εδώ.

Η μέγιστη κινητική ενέργεια…

Σε λείο οριζόντιο επίπεδο, κινούνται στην ίδια ευθεία δύο  σφαίρες Α και Β με ίσες ακτίνες, οι οποίες κάποια στιγμή συγκρούονται κεντρικά και ελαστικά. Δίνεται ότι m_Α=m και m_Β=2m, ενώ πριν την κρούση η Α σφαίρα έχει ταχύτητα μέτρου υ₁ με φορά προς τα δεξιά.

i)  Αν κατά την κρούση η σφαίρα Α αυξάνει την κινητική της ενέργεια, τότε η ταχύτητα της Β σφαίρας πριν την κρούση:

 α) Έχει φορά προς τα δεξιά.

 β) Είναι μηδενική

 γ) έχει φορά προς τα αριστερά.

ii) Αν η σφαίρα Β, μεταφέρει στην Α σφαίρα το 100% της κινητικής της ενέργειας, τότε η ταχύτητά της πριν την κρούση είχε μέτρο:

α) υ₂=υ₁,  β) υ₂=2υ₁,   γ) υ₂=3υ₁.

iii) Στην παραπάνω περίπτωση, η μέγιστη κινητική ενέργεια που αποκτά η σφαίρα Α μετά την κρούση, είναι:

α) Κ_mαx= ½ mυ₁²,   β) Κ_mαx= 4∙ ½ mυ₁²,  γ) Κ_mαx= 8∙ ½ mυ₁²,  δ) Κ_mαx= 9∙ ½ mυ₁².

Απάντηση:

ή

Η μέγιστη κινητική ενέργεια…

Η Ιθάκη … αχνοφαίνεται ακόμη.

Στο διπλανό σχήμα τα δύο ελατήρια έχουν σταθερές k₁ και k₂ = 2k₁. Αρχικά το σύστημα ισορροπεί με το κάθε ελατήριο να είναι παραμορφωμένο κατά Δℓ₁ και Δℓ₂ αντίστοιχα. Στην Θ.Ι. το ελατήριο σταθεράς k₂ έχει διπλάσια δυναμική ενέργεια παραμόρφωσης από το ελατήριο σταθεράς k₁. Ανασηκώνουμε το σώμα Σ μάζας m μέχρι τη θέση όπου το ελατήριο σταθεράς k₂ δεν ασκεί καμιά δύναμη στο σώμα Σ. Από την θέση αυτή αφήνουμε το σώμα να εκτελέσει ταλάντωση σταθεράς D = k₁ + k₂. Η δυναμική ενέργεια της ταλάντωσης τις στιγμές που το ελατήριο σταθεράς k₁ δεν έχει αποθηκευμένη ενέργεια, είναι:

   

Τι κίνηση θα κάνει ο δίσκος;

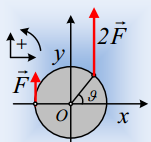
Σε ένα λείο οριζόντιο επίπεδο ηρεμεί ένας ομογενής οριζόντιος δίσκος κέντρου Ο. Σε μια στιγμή στο δίσκο ασκούνται δυο οριζόντιες δυνάμεις όπως στο σχήμα, όπου θ=60°. Στο σχήμα δίνεται ένα σύστημα οριζόντιων ορθογωνίων αξόνων xy, όπου οι δυνάμεις έχουν τη διεύθυνση του άξονα y. Ο δίσκος θα εκτελέσει:

i)   σύνθετη κίνηση προς τη θετική κατεύθυνση του άξονα y και με θετική φορά περιστροφής.

ii)  σύνθετη κίνηση προς τη θετική κατεύθυνση του άξονα y και με αρνητική φορά περιστροφής.

iii) μεταφορική κίνηση προς τη θετική κατεύθυνση του άξονα y.

iv) μεταφορική κίνηση σε  διαφορετική διεύθυνση από αυτές των δύο αξόνων.

Απάντηση:

ή

Τι κίνηση θα κάνει ο δίσκος;

Κόψε το νήμα το γερό να δεις δυο ταλαντώσεις στο …φτερό.

Τα δύο σώματα Σ₁ και Σ₂ είναι δεμένα σε ελατήρια ίδιας σταθεράς k και έχουν μάζες m₁ και m₂ αντίστοιχα για τις οποίες ισχύει m₁ > m₂. Μέσω νήματος έχουμε κρεμάσει κάτω από το σώμα Σ₁ ένα σώμα Σ μάζας m. Τα σώματα Σ και Σ₂ μόλις που δεν ακουμπούν. Κάποια χρονική στιγμή κόβουμε το νήμα που συνδέει τα Σ₁ και Σ, με αποτέλεσμα το Σ₁ και τα Σ₂ – Σ να αρχίσουν να ταλαντώνονται με D = k σε κάθε περίπτωση.

Α. Για τα πλάτη των ταλαντώσεων (Α₁ του Σ₁ και Α₂ των Σ₂ – Σ) ισχύει η σχέση:

α. Α₁ = Α₂                    β. Α₁ >  Α₂                   γ. Α₁ < Α₂

Να επιλέξετε την σωστή απάντηση αιτιολογώντας την επιλογή σας.

Β. Για τις μέγιστες παραμορφώσεις των ελατηρίων ισχύει:

α. Δℓ_1max > Δℓ_2max        β. Δℓ_1max < Δℓ_2max        γ. δεν επαρκούν τα δεδομένα για να απαντήσουμε.

Να επιλέξετε την σωστή απάντηση αιτιολογώντας την επιλογή σας.

Γ. Όταν τα σώματα Σ₂, Σ βρίσκονται στο κατώτερο σημείο της ταλάντωσης τους αφαιρούμε απότομα το Σ. Το πλάτος της νέας ταλάντωσης που θα εκτελέσει το Σ₂ θα:

    

Ας εφαρμόσουμε την αρχή Pascal

Το δοχείο του σχήματος βρίσκεται έξω από την ατμόσφαιρα και περιέχει νερό πυκνότητας ρ και το πλευρικό σωληνάκι διατομής Α κλείνεται με αβαρές έμβολο. Η διάταξη βρίσκεται μέσα στο πεδίο βαρύτητας, όπου η επιτάχυνση της βαρύτητας είναι g. Ασκούμε κάθετα στο έμβολο εξωτερική δύναμη μέτρου F.

1) Η πίεση στο σημείο Γ, που βρίσκεται στο ίδιο οριζόντιο επίπεδο με το κάτω μέρος του εμβόλου είναι 

 ΑΠΑΝΤΗΣΗ

Μηδενίζοντας τη διαφορά πίεσης

Σε κατακόρυφο ροόμετρο Venturi ρέει μόνιμα και στρωτά νερό. Δυο μανόμετρα έχουν προσαρμοστεί στο ροόμετρο στα σημεία 1 και 2, όπως φαίνεται στο σχήμα. Οι αντίστοιχες εγκάρσιες διατομές έχουν λόγο Α1/Α2=5/4 και η υψομετρική διαφορά των σημείων 1 και 2 είναι h. Αν οι ενδείξεις των μανομέτρων είναι ίσες, η ταχύτητα του νερού στη θέση 2 ΕΙΝΑΙ

                                                                                

Δύο δοχεία τρύπησαν…

 

Δυο δοχεία Δ1 και Δ2, κυλινδρικά, με μεγάλη διατομή, περιέχουν διαφορετικά ιδανικά υγρά με πυκνότητες ρ₁ και ρ₂ αντίστοιχα. Μια μικρή τρύπα ανοίγεται στην παράπλευρη επιφάνεια κάθε δοχείου στην ίδια απόσταση h κάτω από την ελεύθερη επιφάνεια του υγρού, ώστε η πρώτη τρύπα να έχει διπλάσια διατομή από την άλλη, δηλαδή Α₁ = 2Α₂.

Αν ο ρυθμός εκροής της μάζας του υγρού είναι ο ίδιος και στα δυο δοχεία

α) Η σχέση μεταξύ των παροχών είναι

ΣΥΝΕΧΕΙΑ

Η μάζα που … "μας φέρνει στα ίσα".

Δύο μη αναμιγνυόμενα υγρά Υ₁ και Υ₂ με πυκνότητες ρ₁ και ρ₂ αντίστοιχα όπου ρ₁ = 3ρ₂ ισορροπούν όπως φαίνεται στο διπλανό σχήμα. Για να φέρουμε τα δύο υγρά στην ίδια στάθμη τοποθετούμε από την μεριά του Υ₂, εφαρμοστό έμβολο μάζας m και εμβαδού της διατομής ίσο με Α. Το έμβολο μπορεί να κινείται χωρίς τριβές, μέσα στον κατακόρυφο σωλήνα. Η μάζα του εμβόλου είναι δίνεται από την σχέση:

α. m = 2ρ₂ΗΑ             β. m = 3ρ₂ΗΑ              γ. m = 4ρ₂ΗΑ

Ρευματική γραμμή και φλέβα.

Στο σχήμα δίνεται ένα τμήμα οριζόντιου σωλήνα, εντός του οποίου ρέει ιδανικό υγρό, με σταθερή παροχή και κάποιες ρευματικές γραμμές του.

i) Η ροή αυτή είναι στρωτή ή τυρβώδης;

ii) Να σημειώστε στο σχήμα τη φλέβα του υγρού η οποία περικλείεται από τις δύο κόκκινες ρευματικές γραμμές του σχήματος, την οποία ας ονομάσουμε φλέβα Χ.

iii) Μια δεύτερη φλέβα Υ περιβάλλεται από τις μπλε ρευματικές γραμμές. Η παροχή είναι μεγαλύτερη στην φλέβα Χ ή στην Υ και γιατί;

iv) Κάποια στιγμή ένα σωμάτιο βρίσκεται στο σημείο Β. Να σχεδιάστε την ταχύτητα του σωματίου αυτού. Μπορεί μετά από λίγο το σωμάτιο αυτό να περάσει από το σημείο Γ;

v) Ένα σωμάτιο Σ₁ σε μια στιγμή t₀ περνάει από το σημείο Α, ενώ τη στιγμή t₁, φτάνει στο σημείο Γ, ενώ στο σημείο Α βρίσκεται πια ένα δεύτερο σωμάτιο Σ₂.

α) Το σωμάτιο Σ₁ ή το Σ₂ έχει μεγαλύτερη ταχύτητα στη θέση Α;

β) Τη στιγμή t₁ ποιο από τα δύο σωμάτια έχει μεγαλύτερη ταχύτητα;

γ) Κατά την μετακίνηση του Σ₁ από το Α στο Β ασκήθηκε πάνω του δύναμη ή όχι; Αν ναι, από πού μπορεί να ασκήθηκε η δύναμη αυτή; Το έργο της δύναμης αυτής είναι θετικό, αρνητικό ή μηδέν;

Να δικαιολογήστε τις απαντήσεις σας.

Απάντηση:

ή

	Ρευματική γραμμή και φλέβα.

Σημαδεμένα θέματα Α

Μία συλλογή Α θεμάτων (πολλαπλής, Σ-Λ, κτλ) που έχουν τεθεί σε πανελλήνιες εξετάσεις και στα διαγωνίσματα της ΟΕΦΕ.
Στο ένα αρχείο υπάρχουν τσεκαρισμένες οι απαντήσεις ώστε να μπορεί εύκολα ο καθηγητής να επαληθεύει γρήγορα τις απαντήσεις (μπορεί κάποια να μου ξέφυγε) ενώ το άλλο αρχείο αφορά μαθητές που θα απαντήσουν.

 

4 Β Θέματα στην μηχανική στερεού + 1 bonus.

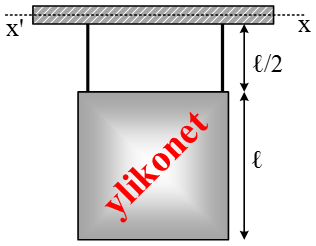Στο διπλανό σχήμα βλέπουμε μία τετράγωνη ταμπέλα μάζας Μ και πλευράς ℓ η οποία είναι κρεμασμένη από σχοινί μήκους ℓ/2. Η ροπή αδράνειας τετράγωνης πλάκας ως προς άξονα που είναι κάθετος στο επίπεδο της και διέρχεται από το κέντρο μάζας της είναι Ι_cm,1 = Mℓ²/6, ενώ η ροπή αδράνειας ράβδου ως προς άξονα που περνά από το κέντρο μάζας της και είναι κάθετος σ’ αυτή είναι Ι_cm,2 = Mℓ²/12.

Αυτά είναι τα Β θέματα από το διαγώνισμα στην μηχανική στερεού από αρχή εώς και ροπή αδράνειας.
Ολόκληρο το διαγώνισμα και οι λύσεις είναι διαθέσιμα εδώ.

Τι θα κάνει ο κύλινδρος;

Γύρω από έναν κύλινδρο βάρους w και ακτίνας R, ο οποίος ηρεμεί σε οριζόντιο επίπεδο, σε επαφή με σκαλοπάτι ύψους h=R/2, έχουμε τυλίξει ένα αβαρές νήμα. Ασκούμε στο άκρο του οριζόντιου νήματος, οριζόντια δύναμη F, μέτρου w/2, όπως στο σχήμα. Αν δεν αναπτύσσονται δυνάμεις τριβής στις επιφάνειες επαφής του κυλίνδρου με το οριζόντιο επίπεδο και το σκαλοπάτι:

i) Να σχεδιάστε τις δυνάμεις που ασκούνται στον κύλινδρο.

ii) Ο κύλινδρος:

 α) Ισορροπεί,

 β) Περιστρέφεται χωρίς να υπερπηδά το σκαλοπάτι.

 γ) Περιστρέφεται ενώ ταυτόχρονα υπερπηδά το σκαλοπάτι.

Απάντηση:

ή

Τι θα κάνει ο κύλινδρος;

Θέμα Β με εξωτερική δύναμη.

Σώμα Σ μάζας m ισορροπεί αρχικά σε οριζόντιο ελατήριο σταθεράς k. Την χρονική στιγμή t₀ = 0 ασκούμε στο σώμα οριζόντια σταθερή δύναμη F με αποτέλεσμα το ελατήριο να επιμηκύνεται. Μόλις το σώμα ακινητοποιηθεί για πρώτη φορά, καταργούμε ακαριαία την δύναμη F και το σώμα εκτελεί μία νέα ταλάντωση.

Α. Το σώμα ξαναπερνά από την θέση φυσικού μήκους την χρονική στιγμή:

  
 

Σώμα δεμένο με νήμα στον τοίχο

Στο διπλανό σχήμα ένα σώμα μάζας m = 2 kg ισορροπεί δεμένο από την μία άκρη του με σχοινί και από την άλλη με ελατήριο του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο σε τοίχο. Το σχοινί έχει μήκος d = 0,1 m και κόβοντας το σώμα μάζας m εκτελεί απλή αρμονική ταλάντωση. Η μέγιστη απόσταση από τον τοίχο που βρίσκεται το σώμα μάζας m κατά τη διάρκεια της ταλάντωσης του είναι d_max = 0,5 m και φτάνει εκεί για πρώτη φορά μετά το κόψιμο του νήματος τη χρονική στιγμή t₁ = 0,05π sec. Να βρεθούν:

α. Ο χρόνος που χρειάζεται το σώμα m για να διανύσει τέσσερις φορές το πλάτος του.

β. Η τάση του νήματος πριν αυτό κοπεί

γ. Το μέτρο της ταχύτητας όταν το σώμα μάζας m απέχει 0,3 m απ’ τον δεξιό τοίχο.

Όταν το σώμα περνά από την θέση ισορροπίας της ταλάντωσης σπάει ο σύνδεσμος μεταξύ σώματος και ελατηρίου.

δ. Να βρεθεί η περίοδος της περιοδικής κίνησης που θα ακολουθήσει θεωρώντας ελαστικές τις κρούσεις με τον τοίχο.

Δίνεται π = 3,14 και π² = 10. Οι διαστάσεις του σώματος θεωρούνται αμελητέες όπως και η διάρκεια της κρούσης. Το ελατήριο είναι ιδανικό.

         

Τα θετικά και τα αρνητικά.

Μια  Καλοκαιρινή βόλτα ακολουθώντας ένα μονοπάτι…

Με 13 σκαλοπάτια!

Ας μιλήσουμε σήμερα για θετικά και αρνητικά μεγέθη, χωρίς να ασχοληθούμε με διανυσματικά φυσικά μεγέθη. Εκεί το πρόσημο είναι αυθαίρετο, αφού καθορίζεται από εμάς μια κατεύθυνση ως θετική, στην προσπάθειά μας να μιλήσουμε με αλγεβρικές τιμές και όχι με τα μέτρα των διανυσμάτων.

Τι ακριβώς σημαίνει ότι ο Α έχει +5€, ενώ ο Β έχει -10€, για να ξεκινήσουμε από ένα παράδειγμα δανεισμένο από την οικονομία;

Θα μπορούσαμε με τον τρόπο αυτό να αποδώσουμε την κατάσταση εκείνη, όπου ο Α έχει 5€, ενώ ο Β όχι απλά δεν έχει χρήματα, αλλά χρωστάει και 10€ ή αν προτιμάτε χρειάζεται και 10€ να πάρει, ώστε να μπορέσει να ξεχρεωθεί.

Το πιο απλό παράδειγμα από το χώρο της επιστήμης που θα μπορούσαμε να αναφέρουμε, είναι το να απαντήσουμε σε πόσο ύψος βρίσκεται ένα σώμα, σε σχέση με την επιφάνεια του τραπεζιού του σχήματος.

Θα μπορούσε η απάντηση να ήταν, ότι η Α σφαίρα βρίσκεται σε μηδενικό ύψος, η Β σφαίρα βρίσκεται 40cm πάνω από το τραπέζι και η Γ 50cm κάτω από την επιφάνεια του τραπεζιού. Αλλά θα μπορούσαμε απλά και να πούμε ότι h_Α=0, h_Β=+40cm και h_Γ=-50cm, όπου h το ύψος από την επιφάνεια  του τραπεζιού. Στην περίπτωση αυτή βέβαια το αρνητικό ύψος της σφαίρας Γ, σημαίνει ότι βρίσκεται χαμηλότερα της επιφάνειας και θα πρέπει να το ανεβάσουμε κατά 50cm ώστε να έρθει στην επιφάνεια.

(Στο παράδειγμα αυτό, σε ένα άλλο επίπεδο διαπραγμάτευσης, θα μπορούσαμε να πάρουμε έναν κατακόρυφο άξονα y, όπου το σημείο της επιφάνειας θα αντιστοιχούσε στην αρχή Ο του άξονα και να μιλούσαμε για τη θέση της σφαίρας y_Β=+40cm και y_Γ=-50cm, αλλά ας μείνουμε απλά στο ύψος h…).

Έτσι αν μιλάμε για τη δυναμική ενέργεια σώματος m=2kg, θεωρώντας ότι η Α σφαίρα στην επιφάνεια του τραπεζιού έχει μηδενική δυναμική ενέργεια, θα είναι:

U_Β=mgh_Β=+8J  και U_Γ=mgh_Γ= -10J.

Όπου η θετική τιμή της στη θέση Β, σημαίνει ότι έχει μεγαλύτερη δυναμική ενέργεια από όση θα είχε πάνω στο τραπέζι ενώ η αρνητική τιμή στη θέση Γ, σημαίνει ότι έχει μικρότερη δυναμική ενέργεια, από όση θα είχε στην επιφάνεια του τραπεζιού.

Ισοδύναμα θα μπορούσαμε να πούμε ότι U_Γ=-10J σημαίνει ότι απαιτείται να προσφέρουμε στο σώμα ενέργεια 10J για να το μεταφέρουμε στην επιφάνεια του τραπεζιού.

Τα θετικά και τα αρνητικά.

Τα θετικά και τα αρνητικά.

Ταχύτητα διάδοσης ενός κύματος.

i)  Το άκρο Ο ενός τεντωμένου ελαστικού νήματος (1), τίθεται σε ταλάντωση, με συχνότητα f οπότε πάνω του διαδίδεται ένα εγκάρσιο αρμονικό κύμα. Η μορφή του νήματος, τη στιγμή που το κύμα φτάνει στο σταθερό άκρο του νήματος, φαίνεται στο πρώτο σχήμα.

Επαναλαμβάνουμε το ίδιο πείραμα με ένα δεύτερο νήμα (2), του ίδιου μήκους και η αντίστοιχη εικόνα είναι αυτή του δεύτερου σχήματος.

Αν υ₁ η ταχύτητα του κύματος στο (1) νήμα και υ₂ η αντίστοιχη ταχύτητα στο νήμα (2) ισχύει:

α) υ₁/υ₂=1,    β) υ₁/υ₂=1,2, γ) υ₁/υ₂=1,4,  δ) υ₁/υ₂=1,6

ii) Το άκρο Ο ενός τεντωμένου ελαστικού νήματος, τίθεται σε ταλάντωση, με συχνότητα f₁ οπότε πάνω του διαδίδεται ένα εγκάρσιο αρμονικό κύμα. Η μορφή του νήματος, τη στιγμή που το κύμα φτάνει στο σταθερό άκρο του νήματος, φαίνεται στο πρώτο σχήμα.

Επαναλαμβάνουμε το ίδιο πείραμα στο ίδιο νήμα, αλλά με συχνότητα ταλάντωσης  f₂  και η αντίστοιχη εικόνα είναι αυτή του δεύτερου σχήματος.

Για τις συχνότητες των δύο κυμάτων ισχύει:

α) f₂/f₁=1,1,         β) f₂/f₁=1,2,         γ) f₂/f₁=1,3,    δ) f₂/f₁=1,4.

Να δικαιολογήστε τις απαντήσεις σας.

Απάντηση:

ή

Ταχύτητα διάδοσης ενός κύματος.