
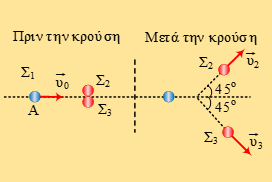
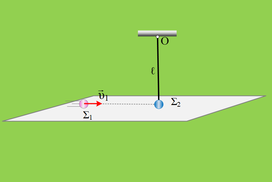
Ένα σώμα Σ1, μάζας m1 = 1 kg, μπορεί να κινείται χωρίς τριβές σε λείο οριζόντιο επίπεδο. Το Σ1 είναι δεμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς k1 = 100 N/m, με το αριστερό άκρο του να είναι στερεωμένο σε ακλόνητο κατακόρυφο τοίχο. Σε απόσταση d1 από τη θέση ισορροπίας του Σ1 και δεξιά αυτής, βρίσκεται ένα ακίνητο σώμα Σ2, μάζας m2, το οποίο μπορεί να κινείται και αυτό στο ίδιο επίπεδο χωρίς τριβές. Δεξιά του σώματος Σ2 και σε απόσταση d2 βρίσκεται το ελεύθερο άκρο οριζοντίου ιδανικού ελατηρίου σταθεράς k2 που έχει το δεξιό του άκρο στερεωμένο σε σώμα Σ3, μάζας m3. Το Σ3 παρουσιάζει τριβή με το οριζόντιο δάπεδο.
Ασκώντας στο σώμα Σ1 κατάλληλη δύναμη συμπιέζουμε το ελατήριο σταθεράς k1 κατά d και στη συνέχεια το αφήνουμε ελεύθερο να εκτελέσει απλή αρμονική ταλάντωση. Μετά από χρονικό διάστημα Δt1 = π/15 s από τη στιγμή που ελευθερώσαμε το σώμα Σ1, αυτό συγκρούεται κεντρικά και ελαστικά με το σώμα Σ2, με αποτέλεσμα το Σ1 αμέσως μετά την κρούση να αρχίσει μία νέα ταλάντωση με μηδενική ταχύτητα. Το σώμα Σ2 μετά την ελαστική κρούση και αφού διανύσει διάστημα d2, προσπίπτει στο ελεύθερο άκρο του ελατηρίου σταθεράς k2. Η στατική τριβή που αναπτύσσεται μεταξύ δαπέδου και σώματος Σ3 το κρατά ακίνητο και το μέτρο της μεγιστοποιείται για πρώτη φορά αφού περάσει χρονικό διάστημα Δt2 = π/40 s μετά την εμφάνισή της. Η γραφική παράσταση της στατικής τριβής φαίνεται στο σχήμα.
Δ1. Να βρείτε τη μάζα του σώματος Σ2 καθώς και το μέτρο της μέγιστης δύναμη που ασκεί το ελατήριο σταθεράς k2 κατά την συμπίεσή του.
Δ2. Τη μέγιστη συσπείρωση του ελατηρίου σταθεράς k2.
Δ3. Να υπολογίσετε την ταχύτητα υ1 του σώματος Σ1 ελάχιστα πριν την κρούση με το Σ2.
Δ4. Να γράψετε την εξίσωση της ταλάντωσης του σώματος Σ1 μετά την κρούση του με το Σ2, θεωρώντας ως t′ = 0 την στιγμή έναρξης της νέας ταλάντωσης.
Δ5. Να υπολογίστε την απόσταση d2 ώστε τα σώματα να ξανασυγκρουσθούν στη θέση ισορροπίας του Σ1 , όταν αυτό διέρχεται από αυτήν για 2η φορά μετά το χάσιμο της επαφής.
Το φετινό διαγώνισμα για τα ΨΕΒ που εκπονήσαμε εγώ και ο Πρόδρομος.
Τα θέματα διαφέρουν λίγο από την αρχική δομή που έτυχε να δουν κάποιοι φίλοι, αλλά έτσι είναι η διαδικασία.
Οι λύσεις προφανώς και υπάρχουν αλλά δεν μπορούν να δημοσιευθούν πριν από την επίσημη ανάρτησή τους στα ΨΕΒ.

 Σώμα Σ1 μάζας
Σώμα Σ1 μάζας 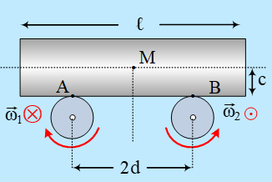 Μία
ομογενής σανίδα με μάζα
Μία
ομογενής σανίδα με μάζα 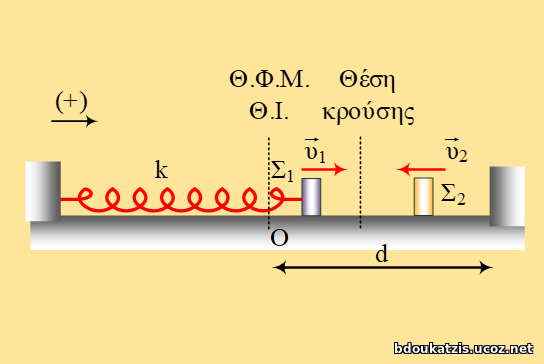




 Κατασκευάζουμε
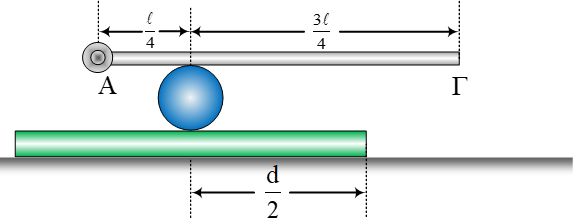
ένα τροχό ενώνοντας τις βάσεις δύο ομογενών κυλίνδρων, έτσι ώστε να αποκτήσουν
κοινό άξονα όπως δείχνει το σχήμα. Ο μεγάλος κύλινδρος έχει ακτίνα R = 0,4 m και
ο μικρός r = 0,2 m. Ο τροχός μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο
άξονα, που ταυτίζεται με τον κοινό γεωμετρικό άξονα των κυλίνδρων. Η ροπή
αδράνειας του συστήματος των ενωμένων κυλίνδρων ως προς τον άξονα αυτό είναι Ι =
0,6 kg∙m². Γύρω από τον μικρότερο κύλινδρο, είναι τυλιγμένο ένα αβαρές σχοινί,
στο κάτω άκρο του οποίου είναι δεμένο ένα σφαιρίδιο Σ μάζας m1 = 7,5
kg. Μια ομογενής δοκός ΑΒ που το βάρος της έχει μέτρο w = 150 Ν, στηρίζεται με
άρθρωση σε κατακόρυφο τοίχο, και εφάπτεται στον μεγάλο κύλινδρο σε απόσταση d =
3ℓ/4 από τη άρθρωση. Το νήμα, δεν γλιστρά κατά την περιστροφή του συστήματος.
Αρχικά συγκρατούμε τον τροχό ακίνητο, και τη χρονική στιγμή t = 0 τον αφήνουμε
ελεύθερο, οπότε αρχίζει το νήμα να ξετυλίγεται. Να υπολογίσετε:
Κατασκευάζουμε
ένα τροχό ενώνοντας τις βάσεις δύο ομογενών κυλίνδρων, έτσι ώστε να αποκτήσουν
κοινό άξονα όπως δείχνει το σχήμα. Ο μεγάλος κύλινδρος έχει ακτίνα R = 0,4 m και
ο μικρός r = 0,2 m. Ο τροχός μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο
άξονα, που ταυτίζεται με τον κοινό γεωμετρικό άξονα των κυλίνδρων. Η ροπή
αδράνειας του συστήματος των ενωμένων κυλίνδρων ως προς τον άξονα αυτό είναι Ι =
0,6 kg∙m². Γύρω από τον μικρότερο κύλινδρο, είναι τυλιγμένο ένα αβαρές σχοινί,
στο κάτω άκρο του οποίου είναι δεμένο ένα σφαιρίδιο Σ μάζας m1 = 7,5
kg. Μια ομογενής δοκός ΑΒ που το βάρος της έχει μέτρο w = 150 Ν, στηρίζεται με
άρθρωση σε κατακόρυφο τοίχο, και εφάπτεται στον μεγάλο κύλινδρο σε απόσταση d =
3ℓ/4 από τη άρθρωση. Το νήμα, δεν γλιστρά κατά την περιστροφή του συστήματος.
Αρχικά συγκρατούμε τον τροχό ακίνητο, και τη χρονική στιγμή t = 0 τον αφήνουμε
ελεύθερο, οπότε αρχίζει το νήμα να ξετυλίγεται. Να υπολογίσετε:
