Τρεις ερωτήσεις για ένα γιο-γιο

 

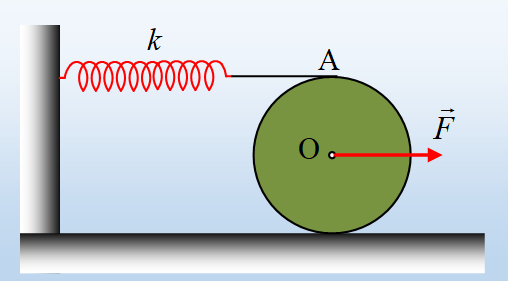
Γύρω από ένα ομογενή κύλινδρο μάζας m και ακτίνας R τυλίγουμε ένα αβαρές νήμα, στο άκρο Α του οποίου ασκούμε μια σταθερή κατακόρυφη δύναμη μέτρου F για t₀=0 και ταυτόχρονα αφήνουμε ελεύθερο τον κύλινδρο να κινηθεί, όπως στο σχήμα. Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής στο Ο,  Ι= ½ mR².

1) Αν F=mg,  ποιες προτάσεις είναι σωστές και ποιες λανθασμένες για τις επιταχύνσεις μόλις αφεθεί ελεύθερος ο κύλινδρος (για t=0⁺):

α) Το σημείο Β, που καταλήγει το νήμα, έχει μηδενική επιτάχυνση.

β) Η επιτάχυνση του σημείου Δ, αντιδιαμετρικού του Β, έχει κατακόρυφη διεύθυνση με φορά προς τα κάτω, μέτρου 2g.

γ) Η επιτάχυνση του σημείου Γ, στο άκρο μιας κατακόρυφης ακτίνας, είναι οριζόντια.

Να δικαιολογήσετε τις απαντήσεις σας.

2) Την χρονική στιγμή που το άκρο Α του παραπάνω νήματος έχει ανέβη κατά h, ο κύλινδρος έχει κινητική ενέργεια:

α) Κ=mgh,    β) Κ= 2mgh,    γ) Κ= 3mgh.

Να δικαιολογήσετε την απάντησή σας.

3) Αν το μέτρο της δύναμης είναι ίσο με F₁= ½ mg, τότε την χρονική στιγμή t:

α) Ποιος ο ρυθμός μεταβολής της στροφορμής του κυλίνδρου ως προς το σημείο Β;

β)  Πόση είναι η  στροφορμή του κυλίνδρου ως προς το Β;

γ) Να βρεθεί η ιδιοστροφορμή του κυλίνδρου ως προς τον οριζόντιο άξονά του ο οποίος περνά από το Ο, καθώς και ο αντίστοιχος ρυθμός μεταβολής της ιδιοστροφορμής.

 

Απάντηση:

ή

 Τρεις ερωτήσεις για ένα γιο-γιο

 Τρεις ερωτήσεις για ένα γιο-γιο

Η κίνηση της ράβδου και ο ρόλος του ελατηρίου

 

Η ομογενής ράβδος ΟΑ μήκους d=5/3m και μάζας m=5,4kg, μπορεί να στρέφεται χωρίς τριβές, κινούμενη σε κατακόρυφο επίπεδο, γύρω από σταθερό οριζόντιο άξονα, ο οποίος περνά από το άκρο της Ο. Η ράβδος συγκρατείται σε οριζόντια θέση, ενώ το άκρο της Α είναι δεμένο στο άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=15Ν/m με φυσικό μήκος l_ο=2/3 m, το άλλο άκρο του οποίου έχει προσδεθεί σε σταθερό σημείο Β, όπως στο σχήμα.

Σε μια στιγμή αφήνουμε τη ράβδο να κινηθεί, οπότε μετά από λίγο γίνεται κατακόρυφη με οριζόντιο το ελατήριο. Ζητούνται:

i)  Η αρχική γωνιακή επιτάχυνση της ράβδου, μόλις αφεθεί να πέσει.

ii) Η ταχύτητα του άκρου Α τη ράβδου, τη στιγμή που αυτή γίνεται κατακόρυφη.

iii) Ο ρυθμός μεταβολής της δυναμικής ενέργειας του ελατηρίου, την στιγμή που γίνεται οριζόντιο.

iv) Θεωρώντας το οριζόντιο επίπεδο το οποίο διέρχεται από το σημείο Β, ως επίπεδο μηδενικής δυναμικής ενέργειας, να υπολογιστεί η μέγιστη μηχανική ενέργεια της ράβδου στη διάρκεια της κίνησής της.

Δίνεται η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της Ι=md²/3 και g=10m/s².

Απάντηση:

ή

 Η κίνηση της ράβδου και ο ρόλος του ελατηρίου

 Η κίνηση της ράβδου και ο ρόλος του ελατηρίου

Όταν τυλίγεται το νήμα, το ελατήριο επιμηκύνεται

   

Ο κύλινδρος του σχήματος, μάζας m=4kg και ακτίνας R=0,1m ηρεμεί σε οριζόντιο επίπεδο. Γύρω του έχουμε τυλίξει ένα αβαρές νήμα, το οποίο συνδέεται με οριζόντιο ιδανικό ελατήριο σταθεράς k=20Ν/m, το οποίο έχει το φυσικό μήκος του, ενώ το άλλο άκρο του έχει στερεωθεί σε κατακόρυφο τοίχο. Σε μια στιγμή στο κέντρο μάζας Ο του κυλίνδρου ασκείται (με κατάλληλο τρόπο) μια σταθερή οριζόντια δύναμη F μέτρου F=23Ν, όπως στο σχήμα, με αποτέλεσμα ο κύλινδρος να κυλίεται και μετά από λίγο, τη στιγμή t₁, ο άξονας του κυλίνδρου να έχει μετατοπισθεί κατά x₁=0,2m. Για την στιγμή αυτή ζητούνται:

i)  Η επιτάχυνση του κέντρου μάζας Ο και η γωνιακή επιτάχυνση του κυλίνδρου.

ii)  Η ενέργεια που έχει μεταφερθεί, μέχρι τη στιγμή αυτή, στον κύλινδρο, μέσω του έργου της δύναμης F, καθώς και η ταχύτητα του ανώτερου σημείου Α του κυλίνδρου.

iii) Η ισχύς της δύναμης F, καθώς και ο ρυθμός με τον οποίο αυξάνεται η κινητική ενέργεια του κυλίνδρου.

iv) Ο ρυθμός μεταβολής της στροφορμής του κυλίνδρου ως προς τον άξονα περιστροφής του κυλίνδρου.

Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής του Ι_cm= ½ mR².

Απάντηση:

ή

 Όταν τυλίγεται το νήμα, το ελατήριο επιμηκύνεται

 Όταν τυλίγεται το νήμα, το ελατήριο επιμηκύνεται

Ένα σύνθετο στερεό και οι ενέργειες

 

Έχουμε κατασκευάσει ένα στερεό s, καρφώνοντας σε έναν ομογενή δακτύλιο μάζας m₁=4kg (η οποία θεωρείται συγκεντρωμένη στην περιφέρειά του) και ακτίνας R=2m, μια ομογενή ράβδο μήκους l=4m και μάζας m₂=6kg, όπως στο σχήμα, όπου το μέσον της ράβδου ταυτίζεται με το κέντρο Ο του δακτυλίου. Τοποθετούμε το στερεό s σε λείο οριζόντιο επίπεδο, με το επίπεδο του δακτυλίου οριζόντιο (το σχήμα σε κάτοψη) και μέσω αβαρούς νήματος, το οποίο έχουμε τυλίξει γύρω από τον δίσκο, ασκούμε την στιγμή t=0 στο στερεό, μια σταθερή οριζόντια δύναμη μέτρου F=12Ν. Την στιγμή t₁=5s, το αντιδιαμετρικό του Α σημείο Β, έχει ταχύτητα μέτρου υ_Β=4m/s, με κατεύθυνση αντίθετη της δύναμης, όπως στο σχήμα.

i)  Να υπολογιστούν την στιγμή t₁, η ταχύτητα του κέντρου μάζας Ο του στερεού s, καθώς και η ταχύτητα του σημείου Α, στο οποίο καταλήγει το νήμα.

ii) Να υπολογιστεί η ροπή αδράνειας της ράβδου, ως προς το κέντρο μάζας της Ο.

iii) Να υπολογιστεί το έργο της ασκούμενης δύναμης F, μέχρι τη στιγμή t₁.

iv) Ποια η στιγμιαία ισχύς της δύναμης F και ποιος ο αντίστοιχος ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου, τη στιγμή t₁.

Η εξίσωση υπολογισμού της ροπής αδράνειας της ράβδου, δεν θεωρείται γνωστή.

Απάντηση:

ή

 Ένα σύνθετο στερεό και οι ενέργειες

 Ένα σύνθετο στερεό και οι ενέργειες

Σέρνοντας μια ρυμούλκα

   

Στο σχήμα βλέπετε μια μικρή ρυμούλκα η οποία έχει προσδεθεί σε αυτοκίνητο και η οποία έχει συνολική μάζα Μ=120kg. Αυτή έχει προφανώς δύο τροχούς, αλλά για τις ανάγκες του προβλήματος θεωρείστε ότι έχει μόνο έναν τροχό μάζας m=40kg και ακτίνας R=0,5m. Σε μια στιγμή ο οδηγός θέτει σε κίνηση το αυτοκίνητο προσδίδοντάς του σταθερή επιτάχυνση α₁=2m/s²,  κινούμενο σε ευθύ οριζόντιο δρόμο, οπότε ο τροχός της ρυμούλκας κυλίεται (χωρίς να ολισθαίνει).

i) Να υπολογιστεί η  δύναμη F, οριζόντιας διεύθυνσης, την οποία ασκεί το αυτοκίνητο στην ρυμούλκα.

ii) Την χρονική  στιγμή t₁=10s, να βρεθούν:

α) Ο ρυθμός με τον οποίο μεταφέρεται ενέργεια από το αυτοκίνητο στην ρυμούλκα.

β) Η κινητική ενέργεια του τροχού, καθώς και ο ρυθμός μεταβολής της κινητικής ενέργειας του τροχού.

γ) Ποιος ο αντίστοιχος ρυθμός μεταβολής της κινητικής ενέργειας του τροχού, λόγω περιστροφής;

iii) Τη στιγμή t₁ ο οδηγός φρενάρει, με αποτέλεσμα το αυτοκίνητο να αποκτήσει σταθερή επιβράδυνση και να μειωθεί η ταχύτητά του στο μισό, σε χρονικό διάστημα Δt=2s. Να υπολογιστεί η δύναμη που δέχεται η ρυμούλκα από το αυτοκίνητο στην διάρκεια του φρεναρίσματος, αν ο τροχός του συνεχίζει να κυλίεται.

Δίνεται η ροπή αδράνειας του τροχού ως προς τον άξονα περιστροφής του Ι= ½ mR².

Απάντηση:

ή

 Σέρνοντας μια ρυμούλκα

 Σέρνοντας μια ρυμούλκα 

Γιο – γιο, μόνο με ενέργειες

 

Γύρω από έναν ομογενή κύλινδρο βάρους w=10Ν έχουμε τυλίξει ένα αβαρές νήμα. Αφήνουμε τη στιγμή t=0 τον κύλινδρο να πέσει κατακόρυφα, ενώ ταυτόχρονα ασκούμε στο άκρο Α του νήματος, μια κατακόρυφη σταθερή δύναμη F, μέτρου F=0,4w. Μετά από λίγο, τη στιγμή t₁, ο κύλινδρος έχει κατέβει κατά y₁=1,5m, ενώ το άκρο Α του νήματος έχει ανέβει κατά y₂=0,5m, όπως φαίνεται στο σχήμα.

i) Να υπολογιστεί η ενέργεια που μεταφέρθηκε στον κύλινδρο από 0-t₁, μέσω του έργου της δύναμης F.

ii) Θεωρώντας την κίνηση του κυλίνδρου ως επαλληλία μιας μεταφορικής και μιας στροφικής κίνησης, να υπολογιστούν η μεταφορική και η περιστροφική κινητική ενέργεια του κυλίνδρου τη στιγμή t₁.

iii) Με βάση τα παραπάνω αποτελέσματα να επιβεβαιώσετε την διατήρηση της ενέργειας, για την κίνηση του κυλίνδρου στο παραπάνω χρονικό διάστημα.

(η ροπή αδράνειας του κυλίνδρου δεν είναι γνωστή).

Απάντηση:

ή

 Γιο – γιο, μόνο με ενέργειες

 Γιο – γιο, μόνο με ενέργειες

Οι κινητικές ενέργειες των σωμάτων

  

 Σε σημείο A ενός δακτυλίου, ακτίνας R=0,5m και μάζας m=1kg, την οποία θεωρούμε συγκεντρωμένη στην περιφέρειά του, έχει στερεωθεί ένα σημειακό σφαιρίδιο της ίδιας μάζας m, δημιουργώντας ένα στερεό S. Το στερεό τοποθετείται σε λείο οριζόντιο επίπεδο και αφήνεται να κινηθεί από την θέση του σχήματος, όπου η ακτίνα ΟΑ σχηματίζει γωνία θ με την οριζόντια διεύθυνση, τη στιγμή t₀=0. Τη στιγμή t₁ που η ακτίνα ΟΑ γίνεται οριζόντια, το σφαιρίδιο έχει ταχύτητα μέτρου υ=2m/s.

i) Να υπολογισθούν την παραπάνω στιγμή t₁:

α) Η ταχύτητα του κέντρου μάζας του στερεού S.

β) Η κινητική ενέργεια του σφαιριδίου

γ) Η κινητική ενέργεια του δακτυλίου.

ii) Η γωνία θ που σχηματίζει η αρχική διεύθυνση της ακτίνας, με την οριζόντια διεύθυνση.

Δίνεται g=10m/s².

Απάντηση:

ή

 Οι κινητικές ενέργειες των σωμάτων

  Οι κινητικές ενέργειες των σωμάτων

Τα έργα και οι ενέργειες σε ένα σύστημα

  

H συμπαγής και ομογενής τροχαλία του σχήματος έχει μάζα Μ =20kg, ακτίνα R =0,2m και φέρει ομόκεντρη κυκλική προεξοχή ακτίνας r = 0,1m. Γύρω από την τροχαλία έχουμε τυλίξει ένα νήμα αμελητέας μάζας (1), στο άκρο Α του οποίου μπορούμε να ασκούμε μια δύναμη F, ενώ γύρω από την προεξοχή έχουμε τυλίξει ένα δεύτερο αβαρές νήμα (2), στο άκρο του οποίου κρέμεται ένα σώμα Σ. Σε μια στιγμή t₀=0 αφήνουμε ελεύθερο το σώμα Σ, ενώ ταυτόχρονα ασκούμε σταθερή δύναμη F=34Ν, στο άκρο Α του πρώτου νήματος, όπως στο σχήμα, οπότε το σώμα Σ ανεβαίνει. Τη στιγμή t₁ το άκρο Α του νήματος έχει ταχύτητα υ_Α=0,8m/s, ενώ η τροχαλία έχει περιστραφεί κατά γωνία θ=2rad.

i) Να υπολογιστεί το έργο της δύναμης F, μέχρι τη στιγμή t₁, καθώς και η ισχύς της δύναμης την στιγμή t₁.
ii) Πόση  είναι η κινητική ενέργεια της τροχαλίας την στιγμή t₁;
iii) Να βρεθεί η ενέργεια που μεταφέρεται μέσω του νήματος, από την τροχαλία στο σώμα Σ.
iv) Να υπολογιστεί η μάζα του σώματος Σ.
Δίνεται η ροπή αδράνειας της τροχαλίας ως προς τον άξονά της Ι= ½ ΜR² και g=10m/s².
Απάντηση:

ή

 Τα έργα και οι ενέργειες σε ένα σύστημα

 Τα έργα και οι ενέργειες σε ένα σύστημα

Η ανύψωση μιας σανίδας.

 

Σε λείο οριζόντιο επίπεδο ηρεμεί μια λεπτή ομογενής σανίδα ΑΒ μήκους 2m και μάζας 3kg. Σε μια στιγμή t=0 στο άκρο Α τη δοκού, ασκούμε μια κατακόρυφη δύναμη, με φορά προς τα πάνω, σταθερού μέτρου F=20Ν. Μετά από λίγο τη στιγμή t₁, η σανίδα έχει ανασηκωθεί, όπως στο σχήμα, σχηματίζοντας με την οριζόντια διεύθυνση γωνία θ, όπου ημθ=0,6 και συνθ=0,8.
i)  Πόση ενέργεια μεταφέρθηκε στη σανίδα μέσω του έργου της δύναμης F, κατά το παραπάνω διάστημα;
ii) Να υπολογιστεί η ταχύτητα του κέντρου μάζας Ο και η γωνιακή ταχύτητα της σανίδας τη στιγμή t₁;
iii) Ποια η ισχύς της δύναμης F τη στιγμή t₁;
Δίνεται η ροπή αδράνειας μιας ομογενούς δοκού ως προς άξονα κάθετο που περνά από το μέσον της Ι_cm= Μℓ²/12, g=10m/s² .

Απάντηση:

ή

 Η ανύψωση μιας σανίδας.

 Η ανύψωση μιας σανίδας.

Ενέργεια αφαιρείται, αλλά και μεταφέρεται

 Παρακάτω θα εξετάσουμε μερικές περιπτώσεις σωμάτων, όπου το έργο κάποιας δύναμης είναι αρνητικό. Τι ακριβώς μετράει το έργο αυτό; Τι σχέση έχουν τα έργα των δυνάμεων δράσης – αντίδρασης, οι οποίες ασκούνται σε δύο σώματα;

 

Εφαρμογή 1^η :

Η σανίδα του σχήματος έχει μάζα Μ=10kg ολισθαίνει σε λείο οριζόντιο επίπεδο με την επίδραση οριζόντιας σταθερής δύναμης F=6Ν. Πάνω στην σανίδα υπάρχει ένα σώμα Σ μάζας m=2kg, το οποίο παρασύρεται κινούμενο μαζί της, χωρίς να ολισθαίνει. Για μετατόπιση των σωμάτων κατά x=4m, να υπολογιστούν:

Συνέχεια…

ή

 Ενέργεια αφαιρείται, αλλά και  μεταφέρεται

 Ενέργεια αφαιρείται, αλλά και  μεταφέρεται

Όταν το νήμα γλιστράει στο αυλάκι της τροχαλίας

 

Η τροχαλία του σχήματος ακτίνας R=0,2m και μάζας Μ=3,5kg μπορεί να στρέφεται χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το κέντρο της Ο. Περνάμε ένα μη εκτατό και αβαρές νήμα από το αυλάκι (ελάχιστου βάθους…) της τροχαλίας και στα άκρα του δένουμε δύο σώματα Α και Β με μάζας m₁=0,2kg και m₂=0,1kg, τα οποία αφήνουμε να κινηθούν, από τις θέσεις που φαίνονται στο σχήμα. Αν το σώμα Α πέφτει με επιτάχυνση α₁=1m/s², να βρεθούν:

i) Η γωνιακή επιτάχυνση που αποκτά η τροχαλία.

ii) Η ενέργεια που μεταφέρεται στο υπόλοιπο σύστημα από το σώμα Α, μέχρι τη στιγμή t₁=2s.

iii) Να αποδείξετε ότι το νήμα γλιστράει στο αυλάκι της τροχαλίας.

iv) Πόση θερμότητα παράγεται λόγω τριβής μεταξύ νήματος και τροχαλίας, μέχρι τη στιγμή t₁.

Δίνεται g=10m/s² και η ροπή αδράνειας της τροχαλίας Ι= ½ ΜR².

Απάντηση:

ή

 Όταν το νήμα γλιστράει στο αυλάκι της τροχαλίας

 Όταν το νήμα γλιστράει στο αυλάκι της τροχαλίας

Μια ράβδος και η κινητική της ενέργεια.

 

Σε λείο οριζόντιο επίπεδο ηρεμεί μια ομογενής ράβδος ΑΒ μάζας m=6kg και μήκους ℓ=4m. Σε μια στιγμή t=0 ασκείται πάνω της μια σταθερή οριζόντια δύναμη, μέτρου F=3Ν, με αποτέλεσμα τη στιγμή t₁=2,14s η ράβδος να έχει περιστραφεί κατά 90°, όπως φαίνεται στο σχήμα (σε κάτοψη). Για τη στιγμή t₁ ζητούνται:

i) Η κινητική ενέργεια της ράβδου.

ii) Η ταχύτητα του άκρου Α της ράβδου.

iii) Ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου.

Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα ο οποίος περνά από το μέσον της Ι=mℓ²/12.

Απάντηση:

ή

 Μια ράβδος και η κινητική της ενέργεια.

 Μια ράβδος και η κινητική της ενέργεια.

Όταν το κιβώτιο μετατρέπεται σε σφαίρα

 

Ο κατακόρυφος οδηγός του σχήματος έχει σχήμα κοίλου τεταρτοκύκλιου ακτίνας R=1,4 m και είναι λείος και ακλόνητος. Ομογενής σφαίρα μάζας m και ακτίνας R=0,15m αφήνεται να ολισθήσει χωρίς τριβές από το άνω άκρο Α και φτάνει στο κάτω άκρο Β, οπότε και εγκαταλείπει τον οδηγό με οριζόντια ταχύτητα υ_Β.

Να βρεθούν :

i)  ο λόγος της γωνιακής ταχύτητας περιστροφής της σφαίρας προς την γωνιακή ταχύτητα περιφοράς της, σε κάθε σημείο της τροχιάς της.

ii)  όταν φτάσει στη θέση Β, ο λόγος της κινητικής μεταφορικής ενέργειας της σφαίρας προς την συνολική κινητική της ενέργεια.

iii) Η ταχύτητα της σφαίρας στο Β.

 Δίνεται g=10m/s².

Απάντηση:

ή

Όταν το κιβώτιο μετατρέπεται σε σφαίρα

 Όταν το κιβώτιο μετατρέπεται σε σφαίρα

Η περιφορά και η περιστροφή ενός δίσκου

 

Στο σχήμα βλέπετε μια αβαρή ράβδο ΓΔ μήκους l=2m, στα άκρα της οποίας έχουν συνδεθεί δύο ομογενείς δίσκοι Α και Β με ακτίνες r=0,5m. Ο δίσκος Α μπορεί να στρέφεται χωρίς τριβές γύρω από άρθρωση στο άκρο Γ της ράβδου, ενώ αντίθετα ο δίσκος Β έχει καρφωθεί, με το κέντρο του να ταυτίζεται με το δεξιό άκρο Δ, χωρίς δυνατότητα περιστροφής, παρά μόνο μαζί με την ράβδο. Ο Α έχει μάζα Μ=12,25kg και στρέφεται ωρολογιακά με γωνιακή ταχύτητα ω₀=4rad/s, ο Β έχει μάζα m=8kg, ενώ η ράβδος συγκρατείται σε οριζόντια θέση. Σε μια στιγμή t₀=0 αφήνουμε το σύστημα να κινηθεί, οπότε η ράβδος ΓΔ στρέφεται, χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το μέσον της Κ. 

i)  Να υπολογιστεί η κινητική ενέργεια  του  δίσκου Β τη χρονική στιγμή t₁=1,3s, όπου η ράβδος γίνεται κατακόρυφη, για πρώτη φορά.

ii) Πόσες περιστροφές έχει εκτελέσει κάθε δίσκος, μέχρι τη στιγμή t₁;

iii) Ποιες οι αντίστοιχες απαντήσεις αν αρχικά ο δίσκος Α ηρεμούσε;

Δίνεται η ροπή αδράνειας ενός δίσκου ως προς κάθετο άξονα ο οποίος διέρχεται από το κέντρο του Ι_cm= ½ mR² και g=10m/s².

Απάντηση:

ή

 Η περιφορά και η περιστροφή ενός δίσκου

 Η περιφορά και η περιστροφή ενός δίσκου

Ανελαστική ή πλαστική κρούση δύο ράβδων

 

Σε λείο οριζόντιο επίπεδο ηρεμούν δύο όμοιες οριζόντιες ομογενείς ράβδοι μήκους l=4m και μάζας m=3kg η καθεμιά. Σε μια στιγμή εκτοξεύουμε την ράβδο ΑΒ με αρχική ταχύτητα υ₀=4m/s κάθετη προς την ράβδο ΓΔ, όπως στο σχήμα, οπότε τη στιγμή της κρούσης οι ράβδοι είναι κάθετες, ενώ συγκρούονται τα άκρα τους Β και Δ.

i)   Αν η ταχύτητα της πρώτης ράβδου ΑΒ μετά την κρούση έχει μέτρο υ₁=2,5m/s, με φορά προς τα δεξιά, η κρούση μεταξύ των δύο ράβδων είναι:

α) Ελαστική,    β) Ανελαστική,    γ) Πλαστική.

ii) Ποια θα ήταν η αντίστοιχη απάντησή σας αν η ταχύτητα της πρώτης ράβδου μετά την κρούση είχε μέτρο υ₁₁=3,2m/s.

Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι_cm= ml²/12.

Απάντηση:

ή

Ανελαστική ή πλαστική κρούση δύο ράβδων

Ανελαστική ή πλαστική κρούση δύο ράβδων

Οι άξονες είναι εύθραυστοι … τώρα τελευταία.

Στο σχήμα βλέπουμε μία ράβδο μάζας m₁ = 6 kg και μήκους ℓ = 1,25 m καθώς επίσης και έναν δίσκο μάζας m₂ και ακτίνας r. Το άκρο Α της ράβδου είναι συνδεδεμένο μέσω άξονα στο κέντρο του δίσκου. Ο δίσκος μπορεί να περιστρέφεται χωρίς τριβές γύρω από τον άξονά του όπως και η ράβδος γύρω από τον δικό της άξονα στο σημείο Γ. Το σύστημα αφήνεται από την οριζόντια θέση και κατά την κάθοδο ο τροχός κυλίεται χωρίς να ολισθαίνει στο δάπεδο σχήματος τεταρτοκυκλίου. Όταν η ράβδος γίνει κατακόρυφη, ο άξονας σύνδεση των δύο στερεών σπάει (χωρίς απώλειες ενέργειας) και ράβδος συνεχίζει την περιστροφή της γύρω από το σημείο Γ, ενώ ο δίσκος εκτελεί οριζόντια βολή από το σημείο που εγκαταλείπει το τεταρτοκύκλιο. Καθόλη την διάρκεια της κοινής κίνησης των δύο στερεών (ράβδος και δίσκος), η κινητική ενέργεια του δίσκου κάθε χρονική στιγμή ήταν μεγαλύτερη κατά 50% από αυτήν της ράβδου. Μετά τον αποχωρισμό η ράβδος ακινητοποιείται στιγμιαία όταν φτάσει σε μία θέση όπου η γωνία θ που σχηματίζει αυτή με την κατακόρυφο είναι τέτοια ώστε το συνημίτονο της να έχει τιμή 1/3. Η ράβδος όταν περνά από την κατακόρυφη θέση έχει βαρυτική δυναμική ενέργεια ως προς το δάπεδο 484,5 J, ενώ ο δίσκος "προσγειώνεται" σε οριζόντια απόσταση – από το κατώτερο μέρος του τεταρτοκυκλίου – s = 6 m. Να βρεθούν:

α. Η στροφορμή της ράβδου τη στιγμή που σπάει ο άξονας ως προς το σημείο Γ.

β. Η μάζα του δίσκου

γ. Το μέτρο της ταχύτητας του κέντρου μάζας του δίσκου τη στιγμή που φτάνει στο έδαφος.

δ. Την μεταβολή της στροφορμής του δίσκου ως προς το κέντρο μάζας του, από την στιγμή t₁ (το στερεό βρίσκεται ακόμη στο τεταρτοκύκλιο) όπου η στροφορμή της ράβδου ως προς το σημείο Γ είναι L_ρ = 6,25 kg∙m²/s, μέχρι τη χρονική στιγμή t₂, όπου ο δίσκος έχει διανύσει οριζοντίως το μισό βεληνεκές του.

Η συνέχεια εδώ.

Τα έργα των δυνάμεων και η κινητική ενέργεια

Σε λείο οριζόντιο επίπεδο ηρεμεί ένας ομογενής  οριζόντιος δίσκος μάζας 20kg και ακτίνας 0,5m. . Τυλίγουμε γύρω του ένα αβαρές και μη εκτατό νήμα, στο άκρο Α του οποίου τη στιγμή t=0 ασκούμε, μια οριζόντια δύναμη μέτρου F₂=10Ν, ενώ ταυτόχρονα στο κέντρο του Ο ασκούμε μια αντιπαράλληλη δύναμη μέτρου F₁=16Ν, όπως στο σχήμα (σε κάτοψη).  Διατυπώνονται δύο προτάσεις:

Α)  Το έργο της δύναμης F₁ μετράει την ενέργεια που μεταφέρεται στο δίσκο και εμφανίζεται με τη μορφή της «μεταφορικής» κινητικής ενέργειας.

Β) Το έργο της δύναμης F₂ μπορεί να υπολογιστεί και ως έργο της ροπής F₂.

Για τον έλεγχο της ορθότητας των παραπάνω προτάσεων, ας δούμε τα παρακάτω ερωτήματα:

Για την κίνηση από τη στιγμή t=0 μέχρι τη στιγμή t₁=10s, να υπολογιστούν:

i)  Η επιτάχυνση του κέντρου μάζας Ο του δίσκου, καθώς και η γωνιακή του επιτάχυνση.

ii) Το έργο της δύναμης F₁ και η αντίστοιχη κινητική ενέργεια, τη στιγμή t₁, η οποία συνδέεται με την μεταφορική κίνηση του δίσκου.

iii) Το έργο της δύναμης F₂ και το αντίστοιχο έργο της ροπής της δύναμης.

iv) Η κινητική ενέργεια του δίσκου τη στιγμή t₁.

Δίνεται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα ο οποίος περνά από το κέντρο του Ο, Ι= ½ mR².

Απάντηση:

ή

 Τα έργα των δυνάμεων και η κινητική ενέργεια

 Τα έργα των δυνάμεων και η κινητική ενέργεια

Ένα ζεύγος περιστρέφει έναν δίσκο

 

Σε λείο οριζόντιο επίπεδο ηρεμεί ελεύθερος ένας ομογενής δίσκος μάζας Μ=20kg και ακτίνας R=2m. Σε μια στιγμή t=0, ασκούμε στα άκρα Α και Β μιας διαμέτρου του, δύο σταθερές αντίθετες δυνάμεις με μέτρα F₁=F₂=14Ν, όπως στο σχήμα (σε κάτοψη).

i)  Να υπολογιστεί η αρχική επιτάχυνση του κέντρου Ο και η αντίστοιχη γωνιακή επιτάχυνση του δίσκου.

Μετά από λίγο τη στιγμή t₁ ο δίσκος έχει στραφεί κατά γωνία φ (ημφ=0,8 και συνθ=0,6), έχοντας γωνιακή ταχύτητα ω₁=1,5rad/s.  Για τη στιγμή αυτή:

ii)  Να βρεθεί η στροφορμή και ο ρυθμός μεταβολής της στροφορμής του δίσκου, ως προς κατακόρυφο άξονα ο οποίος περνά από το κέντρο του Ο.

iii) Να υπολογιστεί η κινητική ενέργεια του δίσκου και ο ρυθμός μεταβολής της κινητικής του ενέργειας.

iv) Μπορείτε να υπολογίστε την στιγμιαία ισχύ της δύναμης F₁ στη στιγμή t₁, χωρίς αναφορά σε ροπή δύναμης ή ροπή ζεύγους δυνάμεων;

Δίνεται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι= ½ ΜR².

Απάντηση:

ή

Ένα ζεύγος περιστρέφει έναν δίσκο

Ένα ζεύγος περιστρέφει έναν δίσκο