Μετά την πλάγια κρούση μια αατ

  

Ένας δίσκος, μάζας m,  ηρεμεί στο πάνω άκρο ενός κατακόρυφου ιδανικού ελατηρίου. Μια  λεία σφαίρα, της ίδιας μάζας, εκτοξεύεται οριζόντια από ένα σημείο Κ, το οποίο βρίσκεται σε κατακόρυφη απόσταση h, πάνω από το δίσκο, οπότε μετά από λίγο συγκρούεται ελαστικά με το δίσκο. Μετά την κρούση βλέπουμε το δίσκο να εκτελεί μια κατακόρυφη απλή αρμονική ταλάντωση.

i) Τι κίνηση θα εκτελέσει η σφαίρα μετά την κρούση με το δίσκο;

ii) Η ενέργεια ταλάντωσης του δίσκου, μετά την κρούση είναι ίση:

α) Ε < mgh,        β) Ε = mgh,                 γ) Ε > mgh.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Μετά την πλάγια κρούση μια αατ

Μετά την πλάγια κρούση μια αατ

Η δοκός και το υλικό σημείο σε περιστροφή

 

Η δοκός του σχήματος, μήκους l=4m, περιστρέφεται γύρω από κατακόρυφο άξονα ο οποίος διέρχεται από το μέσον της Ο, διαγράφοντας οριζόντιο επίπεδο (το σχήμα σε κάτοψη). Στο ένα άκρο της δοκού έχει προσκολληθεί μια μικρή σφαίρα Σ μάζας 0,1kg, δημιουργώντας έτσι ένα στερεό s. Στο διάγραμμα δίνεται η γωνιακή ταχύτητα του στερεού σε συνάρτηση με το χρόνο, όπου η αρχική γωνιακή ταχύτητα έχει την κατεύθυνση που έχει σημειωθεί, ενώ η θέση της δοκού είναι αυτή του σχήματος με τη σφαίρα στη θέση Α.

i)  Τη στιγμή t₁=0,5s να υπολογιστούν η γωνιακή επιτάχυνση του στερεού s, η στροφορμή και ο ρυθμός μεταβολής  τη στροφορμής της σφαίρας Σ, την οποία θεωρούμε υλικό σημείο, ως προς τον άξονα περιστροφής στο Ο.

ii) Αφού υπολογιστεί η γωνία που έχει περιστραφεί το στερεό μέχρι τη  στιγμή t₂=2s να υπολογιστούν για τη στιγμή t₂:

α) Η επιτάχυνση της σφαίρας και η δύναμη που δέχεται από τη δοκό.

β) Ο ρυθμός μεταβολής της στροφορμής της σφαίρας ως προς τον άξονα περιστροφής.

iii) Ποια χρονική στιγμή t₃ η σφαίρα βρίσκεται ξανά  στην θέση Α, για πρώτη φορά; Να υπολογιστεί η μεταβολή της στροφορμής της σφαίρας από 0-t₃.

Απάντηση

ή

 Η δοκός και το υλικό  σημείο σε περιστροφή

 Η δοκός και το υλικό  σημείο σε περιστροφή

Μια διάσπαση σωματιδίου σε μαγνητικό πεδίο

   

Στο σχήμα φαίνεται η τομή ΑΒΓΔ ενός ομογενούς μαγνητικού πεδίου, η ένταση του οποίου είναι κάθετη στο επίπεδο της σελίδας με μέτρο Β=0,01Τ, σχήματος τετραγώνου πλευράς α=10cm.  Σε μια στιγμή ένα σωματίδιο Θ εισέρχεται με ορισμένη ταχύτητα υ, κάθετα στην πλευρά ΓΔ, στο μαγνητικό πεδίο, στο μέσον της Μ. Το σωματίδιο κινείται ευθύγραμμα και μετά από λίγο φτάνει στο κέντρο Κ του τετραγώνου, όπου και διασπάται  σε τρία «σωματίδια- θραύσματα» Χ^-, Υ⁺ και Ζ, τα οποία αποκτούν ταχύτητες υ₁, υ₂ και υ₃ αντίστοιχα, όπου η υ₁ και υ₃ έχουν διεύθυνση παράλληλη στην πλευρά ΑΒ, ενώ η υ₂ είναι κάθετη στην ΑΒ.

i)  Αν το σωματίδιο (Χ^-) βγαίνει από το πεδίο από την κορυφή Α, κάθετα στην πλευρά ΑΒ, να βρείτε την κατεύθυνση της έντασης του πεδίου, δικαιολογώντας την απάντησή σας. Ποιο το μέτρο της ορμής του Χ^- κατά την κίνησή του στο πεδίο;

ii) Να εξηγήσετε γιατί το σωματίδιο Θ είναι αφόρτιστο.

iii) Αν και το σωματίδιο Υ⁺ εξέρχεται από ένα σημείο της πλευράς ΑΒ, να σχεδιάσετε κατ’ εκτίμηση την τροχιά του. Με βάση την σχεδίαση που κάνατε, να συγκρίνεται τις ορμές των σωματιδίων Χ^- και Υ⁺.

iv) Να βρείτε το σημείο εξόδου από το πεδίου για το σωματίδιο Ζ.

v) Αν το σωματίδιο Ζ είναι ένα φωτόνιο, να υπολογιστεί η ενέργειά του.

Δίνεται το στοιχειώδες ηλεκτρικό φορτίο |e|=1,6∙10^-19C,  c=3∙10⁸m/s, ενώ οι ταχύτητες όλων των σωματιδίων (εκτός των φωτονίων...) είναι πολύ μικρότερες της ταχύτητας του φωτός.

Απάντηση:

ή

 Μια διάσπαση σωματιδίου σε μαγνητικό πεδίο

 Μια διάσπαση σωματιδίου σε μαγνητικό πεδίο

Το μαγνητικό πεδίο εξασφαλίζει την ισορροπία

 

Οι δύο λείοι κατακόρυφοι στύλοι xx΄ και yy΄ δεν εμφανίζουν αντίσταση, απέχουν μεταξύ τους κατά d=0,2m, ενώ μια πηγή ΗΕΔ Ε=10V και εσωτερικής αντίστασης r=1Ω συνδέεται στα κάτω άκρα τους x και y. Ένας ομογενής αγωγός ΑΓ, μήκους 0,8m, αντίστασης R=2Ω και βάρους w=2Ν, μπορεί να στρέφεται γύρω από σταθερό οριζόντιο άξονα, ο οποίος περνά από το άκρο του Α. Εκτρέπουμε τον αγωγό ΑΓ κατά γωνία θ=30°, από την κατακόρυφη θέση, φέρνοντάς τον στη θέση που φαίνεται στο σχήμα, σε επαφή με τους κατακόρυφους  στύλους και τον αφήνουμε, παρατηρώντας ότι αυτός ισορροπεί. Αν στο χώρο υπάρχει ένα ομογενές μαγνητικό πεδίο με δυναμικές γραμμές κάθετες στο επίπεδο του σχήματος, μέτρου Β=0,4Τ,  να βρεθούν:

i) Η ένταση του ρεύματος που διαρρέει την πηγή.

ii) Η δύναμη Laplace που ασκείται από το μαγνητικό πεδίο στον αγωγό ΑΓ.

iii) Η απόσταση του άξονα περιστροφής της ράβδου στο άκρο Α, από τον κατακόρυφο αγωγό yy΄.

iv) Η δύναμη που δέχεται ο αγωγός ΑΓ από την άρθρωση στο άκρο της Α.

Απάντηση:

ή

 Το μαγνητικό πεδίο εξασφαλίζει την ισορροπία

 Το μαγνητικό πεδίο εξασφαλίζει την ισορροπία

Η ράβδος σε ισορροπία, παρά την ταλάντωση

 

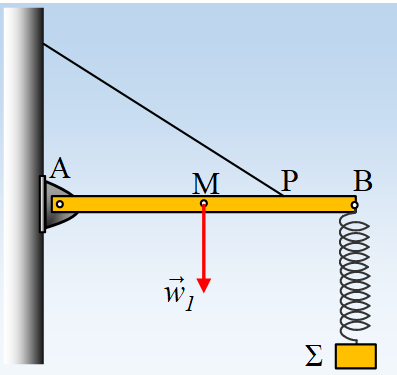
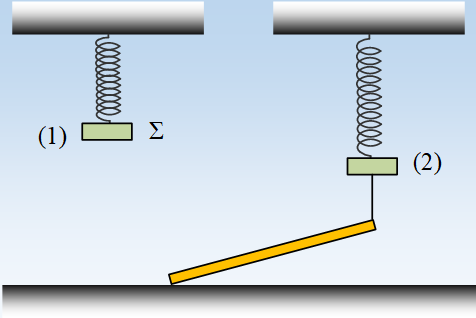
Μια ομογενής ράβδος ΑΒ βάρους w=200Ν, ηρεμεί σε οριζόντια θέση, στηριζόμενη σε τρίποδο στο σημείο Γ,  ενώ δένεται στο άκρο κατακόρυφου νήματος στο σημείο Ο. Στο άκρο Β έχει προσδεθεί ιδανικό κατακόρυφο ελατήριο σταθεράς k=200Ν/m, στο κάτω άκρο του οποίου, ηρεμεί ένα σώμα Σ μάζας m=5kg, όπως στο σχήμα.

i)  Να υπολογιστεί η τάση του νήματος.

ii)  Εκτρέπουμε το σώμα Σ κατακόρυφα προς τα κάτω κατά y₁=0,2m και τη στιγμή t=0, το αφήνουμε ελεύθερο να εκτελέσει αατ. Θεωρώντας την προς τα πάνω κατεύθυνση ως θετική, να βρεθούν οι εξισώσεις και να γίνουν οι γραφικές παραστάσεις:

α) Της δύναμης του ελατηρίου η οποία ασκείται στο σώμα Σ.

β) Της τάσης του νήματος, η οποία ασκείται στη ράβδο.

iii) Επαναλαμβάνουμε το πείραμα, αλλά τώρα εκτρέπουμε το σώμα Σ προς τα κάτω κατά y₂=0,5m και το αφήνουμε να ταλαντωθεί.

α)  Να αποδείξετε ότι θα σπάσει το νήμα και θα καταστραφεί η ισορροπία, πριν το σώμα φτάσει στην άνω ακραία θέση της ταλάντωσής του.

β) Να υπολογιστεί η κινητική ενέργεια του σώματος Σ, τη στιγμή που κόβεται το νήμα.

Δίνεται το όριο θραύσεως του νήματος Τ_θ=120Ν, g=10m/s², π²≈10, ενώ για τις αποστάσεις που βλέπετε στο σχήμα (ΑΟ)=(ΟΚ)=(ΚΓ)=ΓΒ)=1m.

Απάντηση:

ή

 Η ράβδος σε ισορροπία, παρά την ταλάντωση

 Η ράβδος σε ισορροπία, παρά την ταλάντωση

Η δύναμη Laplace σε τετράγωνο πλαίσιο.

 

 Σε ένα ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β, βρίσκεται ένα οριζόντιο τετράγωνο μεταλλικό πλαίσιο, πλευράς ℓ, το οποίο διαρρέεται από ηλεκτρικό ρεύμα έντασης Ι, όπως στο σχήμα, όπου η ένταση του μαγνητικού πεδίου Β είναι παράλληλη στην πλευρά ΑΒ.

i)  Η συνισταμένη  δύναμη που ασκείται από το μαγνητικό πεδίο στο πλαίσιο έχει μέτρο:

α) F=0 ,    β) F= ΒΙℓ,   γ) F= 2ΒΙℓ,   δ) F=4ΒΙℓ.

ii) Η συνολική ροπή η οποία τείνει να περιστρέψει το πλαίσιο, έχει μέτρο:

α) τ=0,  β) τ=ΒΙℓ²,   γ)  τ=2ΒΙℓ²,    δ) τ=4ΒΙℓ².

iii) Να σχεδιάστε στο σχήμα την δύναμη  η οποία ασκείται σε κάθε πλευρά του πλαισίου, καθώς και το  διάνυσμα της συνολικής ροπής ως προς το κέντρο του τετραγώνου.

Να δικαιολογήσετε πλήρως τις απαντήσεις σας.

Απάντηση:

ή

  Η δύναμη Laplace σε τετράγωνο πλαίσιο.

  Η δύναμη Laplace σε τετράγωνο πλαίσιο.

Η αλγεβρική τιμή και το μέτρο της δύναμης

 

Η ομογενής δοκός ΑΒ μάζας Μ, μπορεί να στρέφεται γύρω από άρθρωση στο άκρο της Α και ισορροπεί οριζόντια, όταν στο άκρο της Β κρέμεται μέσω ελατηρίου ένα σώμα Σ, μάζας m, ενώ συγκρατείται μέσω νήματος, το οποίο έχουμε δέσει στο σημείο Ρ, όπως στο σχήμα. Κάποια στιγμή θέτουμε το Σ σε κατακόρυφη ταλάντωση με πλάτος Α=2mg/k.

i)   Θεωρώντας την προς τα πάνω κατεύθυνση ως θετική, η αλγεβρική τιμή της δύναμης του ελατηρίου η οποία ασκείται στο σώμα Σ, σε συνάρτηση της απομάκρυνσης y, δίνεται από την σχέση:

α) F_ελ=-mg+ky,    β) F_ελ=mg-ky,    γ)  F_ελ=-mg-ky

ii)  Αν κατά την παραπάνω ταλάντωση οριακά εξασφαλίζεται η ισορροπία της ράβδου, χωρίς να λυγίζει το νήμα, τότε για τις μάζες Μ και m ισχύει:

α) Μ=m,   β) Μ=2m,    γ) Μ=3m,   δ) Μ=4m.

Απάντηση:

ή

 Η αλγεβρική τιμή και το μέτρο της δύναμης

 Η αλγεβρική τιμή και το μέτρο της δύναμης

Δυο ισορροπίες, η μία με ράβδο

 

Ένα σώμα Σ μάζας m ηρεμεί δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, στη θέση (1) του σχήματος. Δένουμε μέσω νήματος, το σώμα Σ στο άκρο ομογενούς ράβδου μάζας Μ=2m, το άλλο άκρο της οποίας στηρίζεται σε λείο οριζόντιο επίπεδο και αφήνουμε το σύστημα να ταλαντωθεί. Εξαιτίας αποσβέσεων, μετά από λίγο το σώμα Σ ηρεμεί ξανά στη θέση (2).

i)  Στη θέση (2) το ελατήριο είναι κατακόρυφο ή όχι; Να δικαιολογήσετε την απάντησή σας.

ii) Αν U₁ η δυναμική ενέργεια του ελατηρίου στη θέση (1) και U₂ η αντίστοιχη στη θέση (2), ισχύει:

α) U₂=2U₁,   β) U₂=3U₁,   γ) U₂=4U₁,   δ) U₂=5U₁.

iii) Να αποδείξτε ότι η απώλεια της μηχανικής ενέργειας, εξαιτίας των αποσβέσεων, είναι ίση με την αρχική δυναμική ενέργεια του ελατηρίου U₁.

Απάντηση:

ή

  Δυο ισορροπίες, η μία με ράβδο

 Δυο ισορροπίες, η μία με ράβδο

Μια αγώγιμη ράβδος σε μαγνητικό πεδίο

 

Μια λεπτή ομογενής μεταλλική ράβδος ΟΑ, μήκους l=1m και μάζας m=0,3kg, μπορεί να στρέφεται σε κατακόρυφο επίπεδο, χωρίς τριβές, γύρω από οριζόντιο άξονα ο οποίος περνά από το άκρο της Ο. Η ράβδος  τροφοδοτείται από ρεύμα έντασης Ι και ισορροπεί όπως στο σχήμα, σχηματίζοντας γωνία θ με την κατακόρυφη, όπου ημθ=0,8 και συνθ=0,6, χωρίς οι αγωγοί σύνδεσης να επηρεάζουν την ισορροπία της. Στο χώρο υπάρχει ένα οριζόντιο μαγνητικό πεδίο έντασης Β=2Τ (περιοχή κίτρινου χρώματος), εντός του οποίου βρίσκεται η μισή ράβδος.

i)  Να σημειώσετε στο σχήμα την κατεύθυνση του διανύσματος της έντασης του μαγνητικού πεδίου, δικαιολογώντας την κατεύθυνσή της.

ii) Να υπολογιστεί η ένταση του ρεύματος που διαρρέει την ράβδο.

iii) Σε μια στιγμή μεταβάλλουμε την ένταση του ρεύματος στην τιμή Ι₁=2Α, με την ίδια φορά. Να υπολογιστούν αμέσως μετά:

α) Η επιτάχυνση του κέντρου μάζας Κ της ράβδου.

β)  Η δύναμη που ο άξονας ασκεί στη ράβδο.

Δίνονται g=10m/s², ενώ η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της στο άκρο Ο, Ι_ο= 1/3 mR².

Απάντηση:

ή

Μια αγώγιμη ράβδος σε μαγνητικό πεδίο

Μια αγώγιμη ράβδος σε μαγνητικό πεδίο

Ένα γιο – γιο σε ταλάντωση

Ομογενής κύλινδρος Σ₂, (γιο–γιο) ισορροπεί έχοντας το νήμα τυλιγμένο γύρω της πολλές φορές. Η μία άκρη του νήματος είναι στερεωμένη στην οροφή Ο και η άλλη στο σώμα Σ₂, το οποίο ισορροπεί κρεμασμένο από κατακόρυφο ιδανικό ελατήριο σταθεράς Κ=10Ν/m, που είναι στερεωμένο στην οροφή, όπως φαίνεται στο σχήμα 1.

Η μάζα του γιο–γιο είναι m₂=0,8kg και η ακτίνα του R=0,1m. Η ροπή αδράνειας του γιο–γιο, ως προς άξονα που είναι κάθετος στο επίπεδό του και ο οποίος διέρχεται από το κέντρο μάζας του δίνεται από σχέση Ι_cm= ½·m₂·R².

Το σώμα Σ₁ θεωρείται σημειακό αντικείμενο μάζας m₁ =0,1kg. Το νήμα και το ελατήριο έχουν αμελητέες μάζες.

i. Να υπολογίσετε την επιμήκυνση d₀ του ελατηρίου από το φυσικό του μήκος στη θέση που ισορροπεί το σύστημα.

Κατόπιν ανυψώνουμε το σώμα m₁ από τη θέση που ισορροπεί κατά  d₁=0,2m  προς τα πάνω και το αφήνουμε ελεύθερο να κινηθεί μια χρονική στιγμή t που θεωρείται η t=0.

ii. Να βρεθεί η ενέργεια που προσφέρθηκε στο σύστημα για την ανύψωση των σωμάτων.

iii. Να υπολογίσετε την κατακόρυφη απόσταση y₂ του γιο–γιο που θα βρεθεί κάτω από τη θέση ισορροπίας του, τη χρονική στιγμή που μηδενίζεται στιγμιαία η ταχύτητα του σώματος Σ₁ για πρώτη φορά.

iv. Nα βρείτε τη θέση που το σώμα Σ₁ αποκτά μέγιστη ταχύτητα και να την υπολογίσετε.

v. Να βρεθεί ο ρυθμός μεταβολής της δυναμικής ενέργειας του ελατηρίου και ο ρυθμός μεταβολής της βαρυτικής δυναμικής ενέργειας του Σ₁ και του γιο–γιο, τη στιγμή που έχουν μέγιστη ταχύτητα για πρώτη φορά.

vi. Να βρεθεί ο ρυθμός μεταβολής της κινητικής ενέργειας του συστήματος τη στιγμή που τα σώματα αποκτούν μέγιστες ταχύτητες για πρώτη φορά.

+ extra

 

Δίνονται: το μέτρο της επιτάχυνσης της βαρύτητας g=10m/s^2 .

Το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας και είναι συνεχώς τεντωμένο.

Η αντίσταση του αέρα θεωρείται αμελητέα.

Απάντηση

Ισορροπία και κίνηση ενός συστήματος

Το σώμα Σ₁ μάζας m₁=4kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k=250Ν/m. Δένουμε το σώμα με αβαρές και μη εκτατό νήμα, το οποίο αφού περάσουμε από μια τροχαλία, στο άλλο άκρο του δένουμε ένα δεύτερο σώμα Σ₂ μάζας m₂=1kg. Ασκώντας μια κατακόρυφη δύναμη F=90Ν συγκρατούμε ακίνητο το Σ₂ όπως στο σχήμα.

Δίνεται ότι η τροχαλία μπορεί να στρέφεται χωρίς τριβές γύρω από τον άξονά της, έχοντας ροπή αδράνειας Ι= ½ ΜR², το νήμα δεν γλιστρά στο αυλάκι της τροχαλίας, ενώ g=10m/s².

i)  Να υπολογιστεί η δυναμική ενέργεια του ελατηρίου κατά την ισορροπία του συστήματος.

ii) Σε μια στιγμή t₀=0, παύουμε να ασκούμε την δύναμη F. Αν η αρχική επιτάχυνση του σώματος Σ₂ είναι α₀₂=11,25m/s², να βρεθεί η μάζα της τροχαλίας.

iii) Μετά από λίγο, τη στιγμή t₁, μηδενίζεται στιγμιαία η επιτάχυνση του σώματος Σ₂.

α) Να βρεθεί η συνολική κινητική ενέργεια του συστήματος των τριών σωμάτων τη στιγμή t₁.

β) Ποιος ο ρυθμός μεταβολής της στροφορμής της τροχαλίας, ως προς τον άξονά της τη στιγμή t₁;

iv) Αν τη στιγμή t₂ που η ταχύτητα του σώματος Σ₂ γίνει ίση με 2m/s, για δεύτερη φορά, κόψουμε το νήμα που συνδέει τα σώματα, να βρεθούν:

 α) Η ενέργεια της ταλάντωσης  του σώματος Σ₁.

 β) Ποιο από τα παρακάτω ποιοτικά διαγράμματα, μπορεί να παριστά τη στροφορμή της τροχαλίας ως προς τον άξονα περιστροφής της, σε συνάρτηση με το χρόνο;

Να δικαιολογήσετε την επιλογή σας.

Απάντηση:

ή

   Ισορροπία και κίνηση ενός συστήματος

Ισορροπία και κίνηση ενός συστήματος

Τσιγκουνιά στα δεδομένα.

Ένα σώμα Σ μάζας m = 1 kg είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k. Με μία δύναμη μεταβλητού μέτρου ανεβάζουμε πολύ αργά το σώμα μέχρι τη θέση όπου το ελατήριο έχει την ίδια αποθηκευμένη ενέργεια με αυτή που είχε όταν ισορροπούσε. Την χρονική στιγμή t₀ = 0 αφήνουμε το σώμα από την θέση που το είχαμε προηγουμένως ανεβάσει και αυτό εκτελεί ταλάντωση σταθεράς D = k. Η επιτάχυνση του ταλαντούμενου σώματος γίνεται κατά μέτρο ίση με την επιτάχυνση της βαρύτητας για πρώτη φορά την χρονική στιγμή t₁ = π/30 s. Να βρείτε:

α. τον χρόνο που χρειάζεται ώστε να ακινητοποιηθεί το σώμα για πρώτη φορά μετά την έναρξη της ταλάντωσης του

β. την ενέργεια που δαπανήσαμε για να θέσουμε το σώμα σε ταλάντωση

γ. την επιτάχυνση του σώματος (μέτρο και κατεύθυνση) όταν η δυναμική ενέργεια του ελατηρίου είναι 2,42 J

δ. το μέτρο της μέγιστης μεταβολής της βαρυτικής δυναμικής ενέργειας του σώματος κατά την διάρκεια της ταλάντωσης του.

Δίνεται g = 10 m/s², θετική θεωρούμε την φορά προς τα πάνω.

   

Κάποια στιγμή το παιχνίδι τελειώνει… Γ.

Μια μικρή σφαίρα Σ μάζας m₁=0,5kg ηρεμεί στο άκρο κατακόρυφου νήματος, μήκους l=0,9m, το άλλο άκρο του οποίου έχει προσδεθεί σε σταθερό σημείο Ο. Μετακινούμε τη σφαίρα φέρνοντάς την στη θέση Α όπου το νήμα είναι οριζόντιο (αλλά και τεντωμένο) και την αφήνουμε να κινηθεί. Μετά από λίγο το νήμα σχηματίζει γωνία θ=30° με την οριζόντια διεύθυνση, για πρώτη φορά, θέση Β.

i) Να υπολογίστε την τάση του νήματος στη θέση Β, καθώς και τον ρυθμό μεταβολής της γωνιακής ταχύτητας της σφαίρας.

ii) Να βρεθεί η στροφορμή της σφαίρας, καθώς και ο αντίστοιχος ρυθμός μεταβολής της, ως προς το σημείο Ο.

Τη στιγμή που η σφαίρα Σ φτάνει στη θέση Β, το νήμα συναντά ένα καρφί, στο σημείο Κ, όπου (ΟΚ)=x, πάνω στο οποίο το νήμα εκτρέπεται, με αποτέλεσμα μετά από λίγο η σφαίρα να φτάνει στη θέση Γ,  έχοντας οριζόντια ταχύτητα υ₁. Στη θέση αυτή η σφαίρα Σ συγκρούεται κεντρικά και ελαστικά με δεύτερη σφαίρα μάζας m₂=1,5kg η οποία κινείται αντίθετα με ταχύτητα μέτρου υ₂=1m/s. Αμέσως μετά την κρούση, η δεύτερη σφαίρα αποκτά ταχύτητα υ₂΄=1,5m/s με  φορά προς τα δεξιά.

iii) Να υπολογίσετε την ταχύτητα της σφαίρας Σ ελάχιστα πριν και ελάχιστα μετά την κρούση.

iv) Να υπολογιστεί η απόσταση (ΟΚ)=x, στην οποία βρίσκεται το καρφί που εκτρέπει το νήμα.

Δίνεται g=10m/s², ημθ= ½ και συνθ =√3/2.

Απάντηση:

 ή

 Κάποια στιγμή το παιχνίδι τελειώνει… Γ.  

Μια ταλάντωση και μια διπλή τροχαλία

Μια διπλή τροχαλία, αποτελείται από δύο ομόκεντρους ομογενείς δίσκους με ακτίνες r=0,1m και R=0,2m και  μπορεί να στρέφεται γύρω από τον σταθερό οριζόντιο άξονά της. Στην μεγάλη τροχαλία έχουμε τυλίξει ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου μέσω ενός ιδανικού ελατηρίου σταθεράς k=100Ν/m κρέμεται ένα σώμα Σ μάζας m=4kg. Γύρω από την μικρή τροχαλία, έχει τυλιχθεί ένα δεύτερο αβαρές και μη ελαστικό νήμα, το άλλο άκρο του οποίου δένεται σε σταθερό σημείο ενός τοίχου, ώστε το νήμα να είναι οριζόντιο, όπως στο σχήμα, με αποτέλεσμα το σύστημα να ισορροπεί.

i) Να υπολογίσετε την τάση του οριζόντιου νήματος

Εκτρέπουμε το σώμα Σ κατακόρυφα προς τα κάτω κατά y₁ και για t=0, το αφήνουμε να κινηθεί.

ii) Τι τιμές μπορεί να πάρει η αρχική εκτροπή y₁, ώστε στη συνέχεια να μην μηδενιστεί η τάση του οριζόντιου νήματος.

iii) Αν y₁=0,2m, να αποδείξετε ότι το Σ θα εκτελέσει ΑΑΤ και στη συνέχεια να βρείτε πώς μεταβάλλεται η τάση του οριζόντιου νήματος, σε συνάρτηση με το χρόνο, κάνοντας και τη γραφική της παράσταση.

iv) Κάποια στιγμή t₁ κόβουμε το οριζόντιο νήμα. Να βρείτε το ρυθμό μεταβολής της στροφορμής ως προς τον άξονα περιστροφής της τροχαλίας,  του συστήματος τροχαλία-σώμα Σ σε συνάρτηση με το χρόνο, κάνοντας και τη γραφική της παράσταση, για t>t₁.

v) Αν t₁=14π/15 s, ποιος ο ρυθμός μεταβολής της στροφορμής της τροχαλίας ως προς τον άξονα περιστροφής της, αμέσως μόλις κόψουμε το νήμα;

Δίνεται g=10m/s².

Απάντηση:

ή

Μια  ταλάντωση και μια διπλή τροχαλία.

Η κίνηση της πλάκας πάνω στο μηχανέλαιο

Η διπλή τροχαλία του σχήματος αποτελείται από δύο ομόκεντρους ομογενείς δίσκους με ακτίνες

R₁=0,1m και R₂=0,2m και μάζες M₁=2kg και Μ₂=4kg αντίστοιχα. Οι δύο δίσκοι συνδέονται μεταξύ τους έτσι ώστε να περιστρέφονται ως ένα σώμα χωρίς  τριβές, γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο τους και είναι κάθετος στο επίπεδό τους. Η τροχαλία στερεώνεται σε τραπέζι στην επιφάνεια του οποίου έχει στρωθεί λεπτό στρώμα μηχανέλαιου πάχους l=1mm, το οποίο συμπεριφέρεται ως νευτώνειο υγρό με συντελεστή ιξώδους n=0,25Pa·s. Πάνω στο λάδι ηρεμεί μια ξύλινη πλάκα μάζας m₁=lkg σχήματος ορθογωνίου παραλληλεπιπέδου με εμβαδό βάσης A=200cm². Η πλάκα συνδέεται με την τροχαλία στο αυλάκι του μικρού δίσκου της μέσω μη εκτατού και αβαρούς νήματος, (νήμα 1).  Στο αυλάκι του μεγάλου δίσκου της τροχαλίας έχουμε τυλίξει αβαρές και μη εκτατό δεύτερο νήμα, (νήμα 2), στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα μάζας m₂=5kg. 

Συνέχεια εδώ

Δυο ενωμένες πλάκες.

Δύο, ίδιων διαστάσεων, πλάκες από διαφορετικά υλικά Α και Β συγκολλούνται δημιουργώντας μια πλάκα, η οποία αφήνεται στην επιφάνεια του νερού που βρίσκεται σε δοχείο, όπως στο σχήμα. Για τις πυκνότητες των υλικών ισχύει ότι ρ_Α>ρ_Β>ρ, όπου ρ η πυκνότητα του νερού. Τι πρόκειται να συμβεί:

i) Η πλάκα θα επιπλεύσει στο νερό.

ii) Η πλάκα θα βυθιστεί εκτελώντας μεταφορική κίνηση.

iii) Η πλάκα θα βυθιστεί εκτελώντας σύνθετη κίνηση.

Απάντηση:

ή

	Δυο ενωμένες πλάκες.

Ο κύλινδρος, η ισορροπία και η επιτάχυνσή του.

Στο διπλανό σχήμα βλέπετε μια ομογενή δοκό ΒΓ, μήκους ℓ και βάρους w, η οποία μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνά από το σημείο Ο, όπου (ΒΟ)=ℓ/3. Η δοκός ισορροπεί οριζόντια, ενώ στο άκρο της Β κρέμεται, με τη βοήθεια αβαρούς νήματος, ένας κύλινδρος βάρους επίσης w, με τις βάσεις του οριζόντιες, ο οποίος είναι βυθισμένος σε μια λεκάνη με νερό, κατά y=0,2m.

i) Να υπολογίσετε τη δύναμη που ασκεί το νερό στον κύλινδρο, καθώς και την τάση Τ του νήματος που συγκρατεί τον κύλινδρο.

ii) Συγκρατώντας τη δοκό σε οριζόντια θέση, απομακρύνουμε τη λεκάνη με το νερό και σε μια στιγμή αφήνουμε ελεύθερο το σύστημα να κινηθεί. Να βρεθεί η αρχική επιτάχυνση του κυλίνδρου.

iii) Παίρνουμε τον κύλινδρο αυτόν, τυλίγουμε γύρω του ένα αβαρές νήμα και τον τοποθετούμε σε λείο κεκλιμένο επίπεδο κλίσεως θ=30^ο. Ασκούμε στο άκρο Α του νήματος δύναμη παράλληλη στο επίπεδο με μέτρο ίσο με την τάση του νήματος στο i) ερώτημα και αφήνουμε ελεύθερο τον κύλινδρο να κινηθεί.

α) Να υπολογιστεί η επιτάχυνση του σημείου εφαρμογής της δύναμης Α.

β) Να βρεθεί η στροφορμή του κυλίνδρου ως προς τον άξονα περιστροφής του, τη στιγμή που έχει ξετυλιχθεί νήμα μήκους 0,8m.

Δίνονται: Η ροπή αδράνειας μιας δοκού ως προς κάθετο άξονα που περνά από το μέσον της Ι_δ=mℓ²/12, η αντίστοιχη του κυλίνδρου ως τον άξονά του Ι_κ= ½ mR², οι βάσεις του κυλίνδρου έχουν εμβαδόν Α₁=0,05m², η πυκνότητα του νερού ρ=1.000kg/m³ και η επιτάχυνση της βαρύτητας g=10m/s². Η δράση της ατμοσφαιρικής πίεσης  δεν λαμβάνεται υπόψη.

Απάντηση:

ή

	Ο κύλινδρος, η ισορροπία και η επιτάχυνσή του.