Η διαφορική εξίσωση στο κύκλωμα LC, όπως αυτό της ανάρτησης «Λίγα ακόμη για την φόρτιση πυκνωτή», είναι:
Η εξίσωση αυτή γράφεται ισοδύναμα:
Η εξίσωση αυτή είναι 2ης τάξης, μη ομογενής, αφού έχει μη μηδενικό 2ο μέλος.
Λύνουμε την αντίστοιχη ομογενή…
Διαβάστε τη συνέχεια:
Ένας πυκνωτής χωρητικότητας C φορτίζεται από μια πηγή με ΗΕΔ Ε, μέσω αντίστασης και στο σχήμα, δίνονται δύο εκδοχές. Στο (1) κύκλωμα η φόρτιση γίνεται μέσω αντίστασης R, ενώ στο (2) μέσω αντίστασης 2R.
i) Μεγαλύτερο φορτίο αποκτά ο πυκνωτής στο κύκλωμα:
α) (1), β) (2), γ) αποκτά το ίδιο φορτίο.
ii) Μεγαλύτερη ενέργεια για την φόρτιση θα προσφέρει η πηγή, στο κύκλωμα:
α) (1), β) (2), γ) θα προσφέρει ίσα ποσά ενέργειας.
iii) Πόση θερμότητα παράγεται σε κάθε αντίσταση στα δυο κυκλώματα, στη διάρκεια της φόρτισης;
iv) Για καθηγητές: Να γίνει το διάγραμμα του φορτίου του πυκνωτή, σε συνάρτηση με το χρόνο, για τα δύο κυκλώματα, στο ίδιο διάγραμμα.
ή
Για το διπλανό κύκλωμα δίνονται Ε=20V, C=5μF, ενώ ο διακόπτης δ είναι ανοικτός. Κλείνουμε το διακόπτη για t=0 και παρατηρούμε ότι το αμπερόμετρο δείχνει σταθερή ένδειξη Ι=0,2Α.
i) Να σχεδιάστε δύο ποιοτικά διαγράμματα για τις εντάσεις των ρευμάτων που διαρρέουν τις δυο αντιστάσεις, σε συνάρτηση με το χρόνο.
ii) Να υπολογίσετε τις αντιστάσεις R1 και R2.
iii) Σε μια στιγμή t1 ο πυκνωτής φέρει φορτίο q1=40μC. Για τη στιγμή αυτή:
α) Να βρεθούν οι εντάσεις των ρευμάτων που διαρρέουν τους κλάδους του κυκλώματος.
β) Πόση είναι η ΗΕΔ από αυτεπαγωγή που αναπτύσσεται στο ιδανικό πηνίο;
iv) Αν ο χρόνος φόρτισης του πυκνωτή είναι (πρακτικά) ίσος με 5R1C, ενώ ο χρόνος σταθεροποίησης του ρεύματος στο πηνίο, είναι (πρακτικά) ίσος με 5 L/R2, να υπολογιστεί ο ρυθμός μεταβολής της έντασης του ρεύματος που διαρρέει το πηνίο τη στιγμή t1.
ή
Ας δούμε κάποιες εφαρμογές, από διαφορετικά κεφάλαια της ύλης και ας κρατήσουμε κάποια συμπεράσματα…
Εφαρμογή 1η:
Διαβάστε τη συνέχεια…
ή
.png)
Σε λείο οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β, με μάζες m1=1kg και m2=4kg, αντίστοιχα, τα οποία συνδέονται μεταξύ τους i) με ένα αβαρές μη εκτατό νήμα και ii) με ένα ιδανικό ελατήριο, με σταθερά k=20Ν/m και φυσικό μήκος lο=0,3m. Σε μια στιγμή ασκούμε στο σώμα Α μια σταθερή οριζόντια δύναμη, μέτρου F=20N, όπως στα σχήματα και τα σώματα κινούνται προς τα δεξιά.
i) Για την πρώτη περίπτωση, για τη στιγμή t1 που το σώμα Α έχει ταχύτητα u1=4m/s, ζητούνται:
α) Η ταχύτητα του σώματος Β και ο ρυθμός με τον οποίο η δύναμη μεταφέρει ενέργεια στο σώμα Α.
β) Ποια η τάση του νήματος; Να υπολογιστεί η ισχύς της τάσης του νήματος που ασκείται στο σώμα Α, καθώς και ο ρυθμός μεταβολής της κινητικής ενέργειας του Α σώματος
γ) Η ισχύς της τάσης του νήματος που ασκείται στο σώμα Β, καθώς και ο αντίστοιχος ρυθμός μεταβολής της κινητικής του ενέργειας.
ii) Ποιες οι αντίστοιχες απαντήσεις στα παραπάνω υποερωτήματα, για την δεύτερη περίπτωση, με το ελατήριο, για τη στιγμή t2 που το σώμα Α έχει ταχύτητα υ1=4,8m/s, ενώ το ελατήριο έχει μήκος l=0,8m;
Για την απάντησή σας στο γ) ερώτημα, δίνεται ότι το σώμα Β τη στιγμή αυτή έχει ταχύτητα υ2=1,1m/s. Εξάλλου εδώ προφανώς δεν μιλάμε για «τάση» του νήματος, αλλά για δύναμη από το ελατήριο.
Να συγκρίνετε και να σχολιάσετε τα αποτελέσματα.
ή
.png)
Γενικά για τη μέτρηση με βολτόμετρο
Τι ακριβώς δείχνει η ένδειξη ενός βολτομέτρου, το οποίο χρησιμοποιούμε για την μέτρηση μιας τάσης; Μπορεί να μιλάμε συνήθως για ιδανικό βολτόμετρο με άπειρη εσωτερική αντίσταση, αλλά η αλήθεια είναι ότι έχει μια πολύ μεγάλη, αλλά όχι άπειρη εσωτερική αντίσταση, με αποτέλεσμα να διαρρέεται από ρεύμα, όταν συνδέεται σε ένα κύκλωμα. Η δε ένδειξή του δεν είναι παρά η τάση Vv=ΙvRv στα άκρα της εσωτερικής του αντίστασης. Ας το δούμε με βάση τα κυκλώματα στα παρακάτω σχήματα.
Στο (α) σχήμα η πηγή έχει ΗΕΔ Ε και μηδενική εσωτερική αντίσταση. Τότε συνδέοντας το βολτόμετρο, το κύκλωμα διαρρέεται από ρεύμα έντασης:
ή
Με αφορμή τη συζήτηση Διαφορά δυναμικού σε κύκλωμα με ΗΕΔ, ας δούμε διευκρινιστικά κάποια πράγματα, σχετικά με το ηλεκτρικό πεδίο. Είναι ένα ή δύο και πώς προκύπτουν;
Έστω η κυκλική τομή ενός κυλινδρικού μαγνητικού
πεδίου, στο οποίο έχουμε έναν σταθερό ρυθμό μεταβολής του μαγνητικού πεδίου και
ένα κυκλικός αγωγός κέντρου Ο, πάνω στον άξονα του σωληνοειδούς, ο οποίος
περιβάλλει το σωληνοειδές. Στο σχήμα έχει σχεδιαστεί μια κόκκινη κυκλική
γραμμή, η οποία παριστά μια δυναμική γραμμή του επαγωγικού ηλεκτρικού πεδίου
που δημιουργείται, εξαιτίας της μεταβολής του μαγνητικού πεδίου. Από τον νόμο
της επαγωγής παίρνουμε:
ή
Δυο μαθητές της Γ΄ Λυκείου, ο Αντώνης (Α) και ο Βασίλης (Β), συζητούν το θέμα της δυναμικής ενέργειας, προσπαθώντας να βγάλουν άκρη, σε αυτά που διάβασαν τελευταία στο ylikonet.gr.
Ας τους ακούσουμε:
Α: Βασίλη πότε λες ότι ένα σώμα θα έχει δυναμική ενέργεια;
Β: Νομίζω όταν δέχεται μια συντηρητική δύναμη.
Α: Και ποια δύναμη ονομάζεις συντηρητική;
Β: Δεν ξέρω την διαφορά, κάτι διάβασα για δυνάμεις πεδίων που συνδέονται με δυναμική ενέργεια και που είναι, να δεις πώς το διάβασα; Πώς τις λένε; Χωρο… τέτοιες!!!
Α: Χωροεξαρτώμενες εννοείς…
Β: Α!!! μπράβο σου! Αλλά αυτά είναι ψιλά γράμματα, εγώ προτιμώ ό,τι διδάχτηκα στο σχολείο στην Α΄ τάξη. Θυμάσαι; Μια δύναμη που το έργο της σε κλειστή διαδρομή είναι μηδενικό. Μια τέτοια δύναμη, είναι κάθε σταθερή δύναμη. Είναι εύκολη η απόδειξη, την διάβασα πρόσφατα.
Α: Δηλαδή λες Βασίλη, ότι αν ένα σώμα δέχεται μια σταθερή δύναμη, μπορούμε να δεχτούμε ότι έχει δυναμική ενέργεια;
Β: Ναι γιατί όχι; Το φορτίο q στο σημείο Γ του ηλεκτρικού πεδίου γιατί έχει δυναμική ενέργεια, ενώ το σώμα Σ στο λείο οριζόντιο επίπεδο, αν δεχτεί μια σταθερή δύναμη F, να μην έχει δυναμική ενέργεια; Αφού μπορώ να αποδείξω ότι κατά μήκος μιας κλειστής διαδρομής το έργο της δύναμης F είναι μηδέν;
Α: Άρα αν στο σώμα Σ ασκηθεί μια δύναμη F, τότε αμέσως αυτό έχει αποκτήσει ενέργεια;
Β: Νομίζω ναι, όπως και το φορτίο q θα αποκτήσει ακαριαία δυναμική ενέργεια μόλις τοποθετηθεί στο σημείο Γ του ηλεκτρικού πεδίου.
Αν θέλετε την συνέχεια, μπορείτε να την διαβάσετε από:
Μια ακόμη προσπάθεια ανάλυσης!
Σε μια πρόσφατη τοποθέτηση σε διπλανή ανάρτηση, μετέφερα κείμενο από τη «Γενική Φυσική Ι» του Καθηγητή κ. Χανιά πάνω στις συντηρητικές δυνάμεις, όπου αναλυτικά περιγράφει πώς καταλήγουμε στην δυναμική ενέργεια.
Ας το δούμε:
Ας κάνουμε τώρα μια προσπάθεια να ξεδιαλύνουμε το τι ακριβώς μας λέει:
1) Πρέπει να μιλάμε πάντα για ένα σύστημα με δύο ή περισσότερα σώματα. Όχι για ένα μεμονωμένο σώμα. Αν έχεις μόνο ένα σώμα, τότε αυτό, το μόνο που μπορεί να κάνει είναι να κινείται και να έχει κινητική ενέργεια.
2) Σε ένα τέτοιο κλειστό σύστημα (κλειστό σημαίνει ότι το έχουμε απομονώσει από όλο το υπόλοιπο σύμπαν), μπορούμε να εστιάσουμε τώρα σε ένα σώμα Α. Τότε το Α μπορεί να αλληλεπιδρά δεχόμενο μια δύναμη F1, από το υπόλοιπο σύστημα Σ1. Προσοχή το Σ1 το έχουμε κλείσει σε αδιαφανές κιβώτιο κίτρινου χρώματος στο σχήμα.
Το πόσο σπουδαία είναι η θεωρητική μηχανική, δεν περιμένετε να το μάθετε από μένα! Αλλά εγώ θα ήθελα να κάνω μια ακόμη προσπάθεια αποσαφήνισης κάποιων πραγμάτων, επί του πρακτέου. Για την διδασκαλία τη Φυσικής στη δευτεροβάθμια εκπαίδευση…
Έτσι ας αφήσουμε τους ορισμούς που κυκλοφορούν, τα πολύπλοκα μαθηματικά, που πολλές φορές μας μπερδεύουν, και, ας μιλήσουμε συγκεκριμένα. Ποιες συντηρητικές δυνάμεις διδάσκουμε στο σχολείο;
Αν αφήσουμε στην άκρη τις πυρηνικές, διδάσκουμε τις βαρυτικές δυνάμεις, τις ηλεκτροστατικές και τις δυνάμεις των ελαστικών παραμορφώσεων (δύναμη του ελατηρίου). Αυτές τις τρεις κατηγορίες δυνάμεων ονομάζουμε διατηρητικές (συντηρητικές…) και τα έργα αυτών των δυνάμεων συνδέονται με κάποια μορφή δυναμικής ενέργειας. Όταν μιλάμε για μηχανική ενέργεια και για ΑΔΜΕ, μορφές ενέργειας που συνδέονται με αυτές τις δυνάμεις έχουμε. Αν σε ένα σύστημα ασκούνται μόνο τέτοιες δυνάμεις, τότε διατηρείται η μηχανική ενέργεια. Αν σε αυτό υπάρχει διαφωνία, ας διατυπωθεί και ας μην διαβαστεί το κείμενο παρακάτω…
Η συζήτηση τελειώνει εδώ.
Δεν μπορεί ο καθένας μας να θεωρεί οποιαδήποτε δύναμη ως συντηρητική και να την συνδέει με δυναμική ενέργεια και να μιλάει για διατήρηση μηχανικής ενέργειας. Αν το κάνει ουσιαστικά χάνει κάθε νόημα ο ορισμός και η διάκριση της μηχανικής ενέργειας. Ας μιλάμε τότε για ενέργεια και διατήρησή της, αλλά όχι για μηχανική ενέργεια.
Και ας έρθουμε τώρα στις ταλαντώσεις. Το πρώτο που μας ενδιαφέρει είναι ποιες δυνάμεις ασκούνται στο σώμα και είναι υπεύθυνες για την ταλάντωσή του. Ο στόχος μας είναι να καταλήξουμε στην εξίσωση:
ΣF=-Dx (1)
Αφού η εξίσωση αυτή, καθορίζει μονοσήμαντα την επιτάχυνση που θα αποκτήσει το σώμα και στην συνέχεια θα μπορέσουμε να γράψουμε τις γνωστές εξισώσεις x=Α∙ημ(ωt+φ), υ=υ(t) και α=α(t). Ολοκληρώνουμε δηλαδή την κινηματική και δυναμική μελέτη του σώματος που ταλαντώνεται, χωρίς καμιά αναφορά στην φύση των ασκούμενων δυνάμεων. Ας είναι οποιεσδήποτε δυνάμεις και οποιαδήποτε η φύση τους…
Την παραπάνω κίνηση, έχω προτείνει από το 2010 να ονομάζουμε «αρμονική ταλάντωση», στην ανάρτηση:
Υπέρ Κινηματικής ο λόγος, αλλά και μια διδακτική πρόταση…(αατ και αρμονική ταλάντωση)
Δεν θα είχα κανένα πρόβλημα βέβαια να πάρει οποιοδήποτε άλλο όνομα, αρκεί να είναι σαφές, ότι μέχρι εδώ δεν έχουμε μιλήσει για ενέργειες. Είναι μια γενική κίνηση, όπως μια γενική κίνηση είναι η ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση. Και όταν μιλάμε γι΄ αυτήν την κίνηση δεν σκεφτόμαστε μόνο την ελεύθερη πτώση…
Αν θέλουμε να μιλήσουμε για ενέργειες, πρέπει να επιστρέψουμε στην εξίσωση (1). Ποιες δυνάμεις είναι αυτές που μας δίνουν την συνισταμένη αυτή; Ας δούμε στο παρακάτω σχήμα, μερικές περιπτώσεις και τις ασκούμενες δυνάμεις.
Στο πρώτο σχήμα (απλό εκκρεμές) ασκείται στο σώμα το βάρος, δύναμη συντηρητική η οποία συνδέεται με δυναμική ενέργεια (U=mgh). Στο μεσαίο, στην διεύθυνση κίνησης (οι κατακόρυφες δίνουν μηδενική συνισταμένη και δεν καθορίζουν την κίνηση) ασκείται η δύναμη του ελατηρίου και αυτή συντηρητική, η οποία συνδέεται με δυναμική ενέργεια (U= ½ k(Δl)2). Στο δεξιό σχήμα ασκούνται δύο ηλεκτροστατικές δυνάμεις από ακίνητα φορτία, δυνάμεις συντηρητικές, οπότε και η συνισταμένη τους είναι επίσης συντηρητική η οποία συνδέεται με δυναμική ενέργεια (U=kcqq1/r).
Συμπέρασμα, και στις τρεις αυτές περιπτώσεις ορίζουμε δυναμική ενέργεια για την ταλάντωση, αφού η συνισταμένη ΣF είναι συντηρητική, οπότε η κίνηση είναι μια ΑΑΤ (με τα… όλα της). Το ίδιο συμβαίνει και στα παρακάτω σχήματα, όπου στο σώμα δεν ασκείται μια συντηρητική δύναμη, αλλά περισσότερες.
Αλλά αν οι επιμέρους συνιστώσες είναι συντηρητικές και η συνισταμένη θα είναι συντηρητική και θα ορίζεται δυναμική ενέργεια ταλάντωσης U= ½ Dx2.
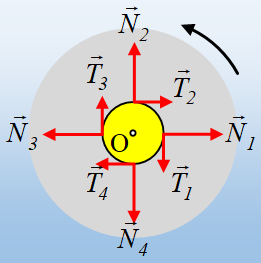
Σχεδιάστε σχήμα με 23 ελατήρια, δύο βαρυτικά πεδία και 34 ακίνητα φορτία, ενώ είναι φορτισμένο το ταλαντούμενο σώμα. Όλες οι δυνάμεις αυτές είναι συντηρητικές, οπότε συντηρητική θα είναι και η συνισταμένη ΣF=-Dx, οπότε ορίζεται η δυναμική ενέργεια ταλάντωσης και η κίνηση είναι ΑΑΤ.
Αν όμως στο σώμα ασκείται για παράδειγμα μια αντίσταση του αέρα, όπως στο σχήμα, τότε η συνισταμένη θα έχει τρεις συνιστώσες, δύο συντηρητικές (w και Fελ) και μια μη συντηρητική (Fαπ=-b∙υ). Αλλά τότε ΔΕΝ διατηρείται η μηχανική ενέργεια και η συνισταμένη δύναμη δεν συνδέεται με κάποια δυναμική ενέργεια, όπου WΣF Α→Β=UΑ-UΒ.
Θα ρωτήσει κάποιος δηλαδή τώρα δεν έχουμε δυναμική ενέργεια ταλάντωσης;
Και βέβαια έχουμε, αλλά αυτή συνδέεται με τις συντηρητικές συνιστώσες (w και Fελ, δηλαδή την δύναμη επαναφοράς -kx και όχι με κάποιο D, το οποίο καθορίζεται και από την μη συντηρητική δύναμη Fαπ. Να θυμίσω ότι στην φθίνουσα ταλάντωση έχουμε μια μικρή αύξηση της περιόδου σε σχέση με την αμείωτη, άλλο αν την προσεγγίζουμε, κατά την διδασκαλία μας).
Έτσι αν φτάσουμε στην εξαναγκασμένη ταλάντωση, όπου επιπλέον ασκείται στο σώμα και μια εξωτερική δύναμη Fεξ από τον διεγέρτη;
Τώρα η συνισταμένη προκύπτει από δύο συντηρητικές δυνάμεις (w και Fελ), όπου η συνισταμένη τους F1=Fελ-w=-kx, είναι επίσης συντηρητική, και συνδέονται με δυναμική ενέργεια U= ½ k∙x2 και δύο μη συντηρητικές (Fεξ, Fαπ), οι οποίες δεν συνδέονται με δυναμικές ενέργειες.
Η κίνηση είναι μια αρμονική εξαναγκασμένη ταλάντωση (μετά τα μεταβατικά φαινόμενα), αλλά δεν είναι η γνωστή μας ΑΑΤ με ενέργεια ταλάντωσης σταθερή και ίση με ½ DΑ2= ½ mω2∙Α2, αφού αυτή η σταθερά D καθορίζεται και από δύο μη συντηρητικές δυνάμεις.
ΥΓ
Νόμιζα ότι το ζήτημα είχε διευκρινιστεί, άσχετα με την θέση που παίρνει ο καθένας μας πάνω στο ζήτημα.
Φαίνεται ότι έκανα λάθος, πράγμα που με οδήγησε στην παρούσα ανάρτηση.
Μέχρι την επόμενη φορά…
