Υπερβολές ενίσχυσης και απόσβεσης κατά τη συμβολή.

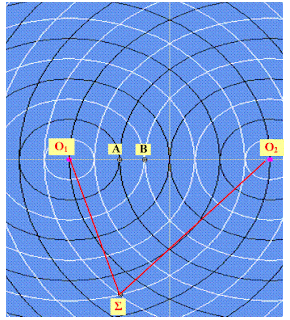
Με αφορμή την ανάρτηση Συμβολή κυμάτων από σύγχρονες πηγές. και τα σχόλια που ακολούθησαν, ας δούμε πιο αναλυτικά ποια σημεία στην επιφάνεια ενός υγρού, στην οποία διαδίδονται δύο κύματα από σύγχρονες πηγές ταλαντώνονται με μέγιστο πλάτος και ποια παραμένουν ακίνητα.

Στην επιφάνεια ενός υγρού διαδίδονται (ας υποθέσουμε με σταθερό πλάτος!!!) δύο κύματα που προέρχονται από δύο σύγχρονες πηγές, με μήκος κύματος λ=20cm.

α)Να βρεθούν τα σημεία που ταλαντώνονται με μέγιστο πλάτος και να σημειωθούν πάνω στο σχήμα, όταν η απόσταση των πηγών είναι:

i)  d= 39cm    ii)  d= 40cm      iii)  d= 41cm,                   iv) 30 cm

β)  Πάνω στα παραπάνω σχήματα να σχεδιαστούν και οι αντίστοιχες γραμμές που να εμφανίζουν τα σημεία που παραμένουν διαρκώς ακίνητα.

Απάντηση.

Υπερβολές ενίσχυσης και απόσβεσης κατά τη συμβολή

Φορτίο και κύλιση

Oι δύο ακίνητες  μεταλλικές φορτισμένες σφαίρες με ακτίνες R₁=R₂=0,1m του παραπάνω σχήματος  έχουν μάζες m₁=1Kg  και m₂=4Kg και φορτία Q₁=10μC  και Q₂=560μC αντίστοιχα  βρίσκονται σε άπειρη μεταξύ τους αρχική απόσταση πάνω σε μονωτικό και άπειρο οριζόντιο επίπεδο. Εκτοξεύουμε την πρώτη σφαίρα με αρχική οριζόντια ταχύτητα υ_o=10m/sec  και κατάλληλη γωνιακή ταχύτητα  έτσι ώστε   η σφαίρα  να αρχίσει αμέσως να κυλίεται χωρίς να ολισθαίνει πάνω στο οριζόντιο επίπεδο πλησιάζοντας τη δεύτερη σφαίρα η οποία μπορεί  να κυλίεται χωρίς να ολισθαίνει συνεχώς. Να βρεθούν:

A)H  απόσταση   των κέντρων μάζας των δύο σφαιρών τη στιγμή που το μέτρο του ρυθμού μεταβολής της στροφορμής την κάθε σφαίρας θα γίνει μέγιστο  αν υποτεθεί ότι το φορτίο τους είναι συνεχώς ισοκατανεμημένο στις εξωτερικές επιφάνειες των δύο σφαιρών.

B)H ηλεκτρική δυναμική ενέργεια των δύο σφαιρών  όταν ο ρυθμός μεταβολής της κινητικής ενέργειας λόγω μεταφορικής κίνησης της πρώτης σφαίρας  γίνει ίσος με το 0.

Nα υποτεθεί ότι το ηλεκτρικό πεδίο γύρω από κάθε σφαίρα είναι περίπου ηλεκτροστατικό και έχει την μορφή ενός πεδίου Coulomb.

Για τις σφαίρες Icm=2/5∙M∙R².

Απάντηση:

Αρμονικό κύμα με αρχική φάση

Εγκάρσιο αρμονικό κύμα πλάτους 4cm και συχνότητας 5Hz, διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου, το οποίο θεωρούμε ότι ταυτίζεται με τον προσανατολισμένο άξονα x΄x, προς τη θετική κατεύθυνση. 

Στο σχήμα δίνεται ένα στιγμιότυπο του κύματος τη χρονική στιγμή t = 0 (τρεις περιπτώσεις), κατά την οποία το κύμα έχει διαδοθεί μέχρι τη θέση x₀. Δίνεται ότι τη χρονική στιγμή t = 0 το υλικό σημείο Ο στη θέση x=0, βρίσκεται σε απομάκρυνση y=-2(3)^0,5 cm από τη θέση ισορροπίας του κινούμενο προς τη θετική κατεύθυνση του άξονα y.

A. Να βρείτε την εξίσωση ταλάντωσης του υλικού σημείου στη θέση x=0.

B. Να υπολογίσετε το μήκος κύματος και την ταχύτητα διάδοσης του κύματος.

C. Να γράψετε την εξίσωση του κύματος.

D. Να παραστήσετε γραφικά τη φάση της απομάκρυνσης (ταλάντωσης)

i.   των υλικών σημείων του θετικού ημιάξονα Οx κατά τη χρονική στιγμή t=1s.

ii.  του υλικού σημείου του μέσου που βρίσκεται στη θέση x=29/3 m, σε συνάρτηση με το χρόνο.

Ε. Να κατασκευάσετε το στιγμιότυπο του κύματος για x≥0 τη χρονική στιγμή 13/12s.

Απάντηση:

Συμβολή κυμάτων από σύγχρονες πηγές.

Στο σχήμα βλέπετε δύο σύγχρονες πηγές O₁ και O₂, οι οποίες απέχουν d=1m, ταλαντώνονται με συχνότητα 10Ηz και παράγουν κύματα στην επιφάνεια ενός υγρού, με πλάτος ταλάντωσης 1cm. Οι λευκοί κύκλοι αποτελούν ισοφασικές γραμμές με φάση 2κπ και οι μαύροι κύκλοι με φάση (2κ+1)π.

i)   Ποια η διαφορά φάσης μεταξύ των δύο κυμάτων που συμβάλουν στο σημείο Α; Ποιο το πλάτος ταλάντωσης του σημείου αυτού;

ii)   Ποιες οι αντίστοιχες απαντήσεις για το σημείο Β;

iii) Πόσο είναι το μήκος κύματος των δύο κυμάτων και πόσα σημεία μεταξύ των δύο πηγών ταλαντώνονται με μέγιστο πλάτος;

iv)  Για το σημείο Σ του σχήματος ποια η διαφορά r₂-r₁ των αποστάσεών του από τις δύο  πηγές; Επιβεβαιώστε, μετρώντας τις δύο αποστάσεις με βάση το σχήμα.

vi) Πόσα τόξα ενισχυτικής συμβολής σχηματίζονται στην επιφάνεια του υγρού;

vii) Αν αυξηθεί η συχνότητα ταλάντωσης των πηγών στην τιμή f₁=12,5Ηz, να σχεδιάστε τα τόξα ενισχυτικής συμβολής στην επιφάνεια του υγρού, μεταξύ των δύο πηγών.

Μπορείτε να παρακολουθήσετε σε ένα αρχείο Applet το φαινόμενο της συμβολής, μεταβάλλοντας τα μήκη κύματος  ή την απόσταση των πηγών και από ΕΔΩ.

Απάντηση:

Συμβολή κυμάτων από σύγχρονες πηγές.

ΤΡΕΧΟΝ ΚΥΜΑ ΚΑΙ ΣΤΙΓΜΙΟΤΥΠΟ

Σ Υ Ν Ε Χ Ε Ι Α >>>>

Κύλιση φορτισμένης σφαίρας.

Στο παρακάτω σχήμα φαίνονται δύο όμοιες σφαίρες ακτίνας R=0,01m μάζας m=4∙10^-4Kg που είναι φορτισμένες με φορτίο Q₁=4∙10^-6C η κάτω σφαίρα και με Q₂=2∙10^-8C η πάνω σφαίρα. H κάτω σφαίρα είναι στερεωμένη πάνω στο  κεκλιμένο επίπεδο γωνίας κλίσης φ=30^ο  από μονωτικό υλικό. Η αρχική απόσταση των δύο κέντρων των σφαιρών είναι d=0,9m.

H πάνω σφαίρα αφήνεται ελεύθερη και σε όλη την διάρκεια της κίνησής της κυλάει χωρίς να ολισθαίνει. Να βρεθούν:

A)   H ελάχιστη απόσταση των δύο κέντρων των δύο σφαιρών αν υποτεθεί ότι το φορτίο των δύο σφαιρών είναι συνεχώς ισοκατανεμημένο στις εξωτερικές επιφάνειες των δύο σφαιρών.

Β)   Την  ολική κινητική ενέργεια της σφαίρας όταν η σφαίρα δέχεται  κάθετη δύναμη από το  κεκλιμένο δάπεδο.

Γ)   Πόσες περιστροφές έχει διαγράψει η σφαίρα μέχρι να σταματήσει για πρώτη φορά.

Υ.Σ.  Τα νούμερα στην άσκηση είναι δανεισμένα από την άσκηση 3.100 του σχολικού βιβλίου της Β Λυκείου θετικής και τεχνολογικής κατεύθυνσης των Α.Ιωάννου,Γ Ντάνου,Α.Πήττα και Σ.Ράπτη.

Απάντηση:

Ένα στιγμιότυπο κύματος.

Ένα κύμα διαδίδεται προς τα δεξιά (θετική κατεύθυνση) κατά μήκος ενός γραμμικού ελαστικού μέσου και στο παρακάτω σχήμα δίνεται ένα τμήμα του στιγμιότυπου κάποια στιγμή, που θεωρούμε t=0, σε μια περιοχή του μέσου, μεταξύ των σημείων Β και Ε. Δίνεται ότι τη στιγμή αυτή τα σημεία Δ και Ε έχουν μηδενική ταχύτητα ταλάντωσης.

Το σημείο Ο στη θέση x=0, θα φτάσει για πρώτη φορά σε απομάκρυνση 0,5m τη χρονική στιγμή t₁=0,3s.

i)  Να σημειώστε πάνω στο σχήμα τις ταχύτητες των σημείων Β, Ο και Γ τη στιγμή που ελήφθη το παραπάνω στιγμιότυπο.

ii) Να υπολογίσετε το πλάτος του κύματος, το μήκος κύματος και την ταχύτητα διάδοσης του κύματος.

iii)  Να υπολογιστεί η επιτάχυνση του σημείου Δ, για t=0.

iv)  Να εξετάσετε αν το κύμα αυτό μπορεί να περιγραφεί από μια εξίσωση της μορφής:

v) Να σχεδιάστε ένα στιγμιότυπο του κύματος αυτού, για την ίδια περιοχή, τη χρονική στιγμή t₂=0,1s.

Απάντηση

Ένα στιγμιότυπο κύματος

Μια πηγή και δύο κύματα.

Στη θέση x_Ρ=6m ενός γραμμικού ελαστικού μέσου υπάρχει μια πηγή κύματος Ρ, η οποία για t=0, αρχίζει να ταλαντώνεται σύμφωνα με την εξίσωση y=1∙ημ(2πt) (μονάδες στο S.Ι.). Η μορφή του μέσου μετά από λίγο, τη στιγμή t₁, είναι αυτή του παρακάτω σχήματος.

i)  Πόσο είναι το πλάτος του κύματος και πόσο το μήκος του κύματος, με βάση την παραπάνω εικόνα;;

ii)  Να βρεθεί η στιγμή t₁ στην οποία ελήφθη η παραπάνω εικόνα.

iii) Να βρεθούν οι εξισώσεις των κυμάτων, y₁=f(t,x) και  y₂=f(t,x), για τα δύο κύματα που κινούνται προς τα δεξιά και προς τ’ αριστερά αντίστοιχα.

iv)  Να σχεδιάστε τη μορφή του μέσου τη χρονική στιγμή t₂=1,5s.

Απάντηση:

Μια πηγή και δύο κύματα

Ταλάντωση φορτίου ανάμεσα σε δύο άλλα

Με αφορμή την άσκηση του Ιωσήφ (ΕΔΩ), ανεβάζω μια παρόμοια, όπου το φορτισμένο σωματίδιο ταλαντώνεται πάνω στην ευθεία των δύο άλλων.
(Μάλλον βρήκα παιχνίδι την προσέγγιση με αατ ...!!)

Η συνέχεια ΕΔΩ ...

ΣΤΙΓΜΙΟΤΥΠΟ ΚΥΜΑΤΟΣ ΚΑΙ ΑΡΧΙΚΗ ΦΑΣΗ

Αρμονικό κύμα με μήκος κύματος λ και πλάτος Α διαδίδεται κατά μήκος ελαστικού μέσου xx' από αριστερά προς τα δεξιά με ταχύτητα μέτρου υ. Τη χρονική στιγμή t=0 το κύμα βρίσκεται στη θέση Σ αριστερά της θέσης Ο (x=0) με xΣ=-λ/2. ΣΥΝΕΧΕΙΑ

Ένα κύμα προς τ’ αριστερά και η εξίσωσή του. Φύλλο εργασίας.

Στο παρακάτω σχήμα βλέπεται τη μορφή ενός αρμονικού κύματος το οποίο  διαδίδεται προς τα αριστερά κατά μήκος ενός γραμμικού ελαστικού μέσου, κάποια στιγμή, για την οποία θεωρούμε ότι   t=0. Κάθε σημείο του μέσου χρειάζεται χρόνο 0,5s για να κινηθεί μεταξύ των δύο ακραίων θέσεων της τροχιάς του.

i)   Με βάση την παραπάνω εικόνα, πόσο είναι το πλάτος και πόσο το μήκος του κύματος;

Μπορείτε να κατεβάσετε το φύλλο κάνοντας κλικ 

εδώ.

Ένα κύμα προς τα’ αριστερά και η εξίσωσή του. Φ.Ε.