Μια κρούση και τα έργα της δύναμης του ελατηρίου

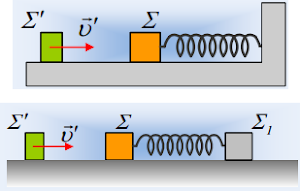
Ένα σώμα Σ μάζας m=1kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=100Ν/m, το άλλο άκρο του οποίου έχει δεθεί σε κατακόρυφο τοίχο, όπως στο πρώτο σχήμα.

Σε μια στιγμή (t=0) ένα δεύτερο σώμα Σ΄ μάζας 0,5kg κινούμενο κατά τη διεύθυνση του άξονα του ελατηρίου, με ταχύτητα υ΄=3m/s συγκρούεται κεντρικά και ελαστικά με το Σ. Η διάρκεια της κρούσης θεωρείται αμελητέα.

i)   Ποια χρονική στιγμή t₁ θα μηδενιστεί για πρώτη φορά η ταχύτητα του Σ και σε πόση απόσταση από την αρχική του θέση θα συμβεί αυτό; Να υπολογιστεί το έργο της δύναμης του ελατηρίου στο παραπάνω χρονικό διάστημα.

Επαναλαμβάνουμε την ίδια κρούση, αλλά τώρα το δεξιό άκρο του ελατηρίου δεν έχει δεθεί σε τοίχο, αλλά σε ένα σώμα Σ₁ μάζας m, όπως στο 2^ο σχήμα. Αν κάποια στιγμή t₂ τα σώματα Σ και Σ₁ έχουν ίσες ταχύτητες:

ii)  Ποιο το μέτρο της ταχύτητας των Σ και Σ₁ τη στιγμή t₂; Να υπολογιστεί το έργο της δύναμης του ελατηρίου που ασκείται σε κάθε σώμα, στο χρονικό διάστημα 0-t₂, όπως και η δυναμική ενέργεια του ελατηρίου τη στιγμή t₂. Ποιος ο ρυθμός μεταβολής της δυναμικής ενέργειας του ελατηρίου τη στιγμή αυτή;

iii)^* Ποια χρονική στιγμή θα μηδενιστεί στιγμιαία η ταχύτητα του σώματος Σ; Να γίνει η γραφική παράσταση υ=υ(t) της ταχύτητας του σώματος Σ σε συνάρτηση με το χρόνο, μετά την κρούση.

^* To iii) ερώτημα δεν απευθύνεται σε μαθητές.

Απάντηση.

ή

Μια κρούση και τα έργα της δύναμης του ελατηρίου