Προς τα πού θα στραφεί;

Μια λεπτή ομογενής ράβδος ΑΒ μάζας 2m μπορεί να στρέφεται γύρω από σταθερό οριζόντιο άξονα που περνά από το σημείο της Ρ, όπου (ΑΡ)= ¼ (ΑΒ), ενώ στα  δυο άκρα της κρέμονται μέσω νημάτων δύο σώματα. Το Σ₁ μάζας m και το Σ₂ μάζας 4m. Το σύστημα συγκρατείται ώστε η ράβδος να είναι οριζόντια. Σε μια στιγμή αφήνουμε ελεύθερο το σύστημα να κινηθεί.

Η ράβδος θα:

i) περιστραφεί δεξιόστροφα

ii) περιστραφεί αριστερόστροφα

iii) ισορροπήσει.

Απάντηση:

ή

Προς τα πού θα στραφεί;

Πόση είναι η ισχύς της αντλίας; Ένα δεύτερο θέμα.

Η αντλία του σχήματος ανεβάζει νερό, μέσω σωλήνα διατομής Α με σταθερή παροχή Π.

Πόση είναι η ισχύς της;

Απάντηση:

Κάποια στιγμή το παιχνίδι τελειώνει… Γ.

Μια μικρή σφαίρα Σ μάζας m₁=0,5kg ηρεμεί στο άκρο κατακόρυφου νήματος, μήκους l=0,9m, το άλλο άκρο του οποίου έχει προσδεθεί σε σταθερό σημείο Ο. Μετακινούμε τη σφαίρα φέρνοντάς την στη θέση Α όπου το νήμα είναι οριζόντιο (αλλά και τεντωμένο) και την αφήνουμε να κινηθεί. Μετά από λίγο το νήμα σχηματίζει γωνία θ=30° με την οριζόντια διεύθυνση, για πρώτη φορά, θέση Β.

i) Να υπολογίστε την τάση του νήματος στη θέση Β, καθώς και τον ρυθμό μεταβολής της γωνιακής ταχύτητας της σφαίρας.

ii) Να βρεθεί η στροφορμή της σφαίρας, καθώς και ο αντίστοιχος ρυθμός μεταβολής της, ως προς το σημείο Ο.

Τη στιγμή που η σφαίρα Σ φτάνει στη θέση Β, το νήμα συναντά ένα καρφί, στο σημείο Κ, όπου (ΟΚ)=x, πάνω στο οποίο το νήμα εκτρέπεται, με αποτέλεσμα μετά από λίγο η σφαίρα να φτάνει στη θέση Γ,  έχοντας οριζόντια ταχύτητα υ₁. Στη θέση αυτή η σφαίρα Σ συγκρούεται κεντρικά και ελαστικά με δεύτερη σφαίρα μάζας m₂=1,5kg η οποία κινείται αντίθετα με ταχύτητα μέτρου υ₂=1m/s. Αμέσως μετά την κρούση, η δεύτερη σφαίρα αποκτά ταχύτητα υ₂΄=1,5m/s με  φορά προς τα δεξιά.

iii) Να υπολογίσετε την ταχύτητα της σφαίρας Σ ελάχιστα πριν και ελάχιστα μετά την κρούση.

iv) Να υπολογιστεί η απόσταση (ΟΚ)=x, στην οποία βρίσκεται το καρφί που εκτρέπει το νήμα.

Δίνεται g=10m/s², ημθ= ½ και συνθ =√3/2.

Απάντηση:

 ή

 Κάποια στιγμή το παιχνίδι τελειώνει… Γ.  

3ωρο Διαγώνισμα στη Φυσική Γ΄Λυκείου (εφ' όλης της ύλης)

Α1) Σώμα μάζας που κάνει Α.Α.Τ., συγκρούεται στη θέση ισορροπίας του ,κεντρικά και πλαστικά, με άλλο σώμα μάζας  ,που κάνει κι αυτό  Α.Α.Τ στην ίδια διεύθυνση, με την ίδια θέση ισορροπίας και την ίδια περίοδο. Για να ακινητοποιηθεί το συσσωμάτωμα αμέσως μετά την κρούση πρέπει να ισχύει για τα πλάτη Α₁ και Α_2......

Τα θέματα:
Οι απαντήσεις:    

Μια ταλάντωση και μια διπλή τροχαλία

Μια διπλή τροχαλία, αποτελείται από δύο ομόκεντρους ομογενείς δίσκους με ακτίνες r=0,1m και R=0,2m και  μπορεί να στρέφεται γύρω από τον σταθερό οριζόντιο άξονά της. Στην μεγάλη τροχαλία έχουμε τυλίξει ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου μέσω ενός ιδανικού ελατηρίου σταθεράς k=100Ν/m κρέμεται ένα σώμα Σ μάζας m=4kg. Γύρω από την μικρή τροχαλία, έχει τυλιχθεί ένα δεύτερο αβαρές και μη ελαστικό νήμα, το άλλο άκρο του οποίου δένεται σε σταθερό σημείο ενός τοίχου, ώστε το νήμα να είναι οριζόντιο, όπως στο σχήμα, με αποτέλεσμα το σύστημα να ισορροπεί.

i) Να υπολογίσετε την τάση του οριζόντιου νήματος

Εκτρέπουμε το σώμα Σ κατακόρυφα προς τα κάτω κατά y₁ και για t=0, το αφήνουμε να κινηθεί.

ii) Τι τιμές μπορεί να πάρει η αρχική εκτροπή y₁, ώστε στη συνέχεια να μην μηδενιστεί η τάση του οριζόντιου νήματος.

iii) Αν y₁=0,2m, να αποδείξετε ότι το Σ θα εκτελέσει ΑΑΤ και στη συνέχεια να βρείτε πώς μεταβάλλεται η τάση του οριζόντιου νήματος, σε συνάρτηση με το χρόνο, κάνοντας και τη γραφική της παράσταση.

iv) Κάποια στιγμή t₁ κόβουμε το οριζόντιο νήμα. Να βρείτε το ρυθμό μεταβολής της στροφορμής ως προς τον άξονα περιστροφής της τροχαλίας,  του συστήματος τροχαλία-σώμα Σ σε συνάρτηση με το χρόνο, κάνοντας και τη γραφική της παράσταση, για t>t₁.

v) Αν t₁=14π/15 s, ποιος ο ρυθμός μεταβολής της στροφορμής της τροχαλίας ως προς τον άξονα περιστροφής της, αμέσως μόλις κόψουμε το νήμα;

Δίνεται g=10m/s².

Απάντηση:

ή

Μια  ταλάντωση και μια διπλή τροχαλία.

221. ΘΕΜΑ Β Στερεό

Β1.  

 Το σχήμα  δείχνει ένα δακτύλιο που έχει ακτίνα R=0,5m και μάζα m. Στο εσωτερικό του δακτυλίου είναι κολλημένη μια σημειακή μάζα m.  Τη στιγμή μηδέν, που τα δύο σώματα είναι ακίνητα όπως φαίνεται στο σχήμα, δίνεται στο δακτύλιο μια αρχική ταχύτητα υ₀ και αυτός κυλίεται χωρίς να παρατηρείται κάποια ολίσθηση γύρω από σταθερό οριζόντιο άξονα, κάθετο στο επίπεδο του δακτυλίου που διέρχεται από το σημείο Κ. Η ελάχιστη αρχική οριζόντια ταχύτητα υ₀ για την οποία ο δακτύλιος θα κάνει πλήρη περιστροφή είναι:

Συνοπτική λύση:  

Δυνάμεις από και προς… σε κύλινδρο που ισορροπεί

Ένας κύλινδρος Α βάρους w ισορροπεί βυθισμένος σε υγρό, όπως στο διπλανό σχήμα (θέση (1)), όπου το μισό ύψος του είναι έξω από το υγρό. Προκειμένου να τον βυθίσουμε πλήρως, τοποθετούμε πάνω του έναν δεύτερο κύλινδρο Β. Το πείραμα προφανώς πραγματοποιείται εντός της ατμόσφαιρας (δεν θα μπορούσε άλλωστε να συμβεί και διαφορετικά…)

i) Η δύναμη που ασκεί ο κύλινδρος Α στο υγρό στη θέση (1) είναι:

α) μικρότερη του βάρους w,

β) ίση με το βάρος,

γ) μεγαλύτερη από το βάρος του κυλίνδρου.

ii) Στη θέση (2) το υγρό ασκεί στον κύλινδρο Α δύναμη μέτρου:

α) F₁=w,  β) F₁=2w,  γ) F₁>2w

Απάντηση:

ή

Δυνάμεις από και προς… σε κύλινδρο που ισορροπεί

Μια κρούση ράβδου με υλικό σημείο

Ένα υλικό σημείο Σ μάζας m είναι δεμένο στο άκρο νήματος μήκους ℓ, το άλλο άκρο του οποίου είναι δεμένο σε σταθερό οριζόντιο άξονα Ο. Γύρω από τον ίδιο άξονα μπορεί να στρέφεται χωρίς τριβές και μια ομογενής λεπτή ράβδος (ΟΑ) της ίδιας μάζας και μήκους επίσης ℓ. Αφήνουμε ταυτόχρονα τα δυο σώματα να κινηθούν σε κατακόρυφο επίπεδο, από την οριζόντια θέση, όπως στο σχήμα.

i) Το σώμα Σ θα συγκρουστεί με το άκρο Α της ράβδου:

  α) στην κατακόρυφη θέση (1),   β) δεξιά της θέσης (1),   γ) αριστερά της θέσης (1)

ii) Ελάχιστα πριν την κρούση μεγαλύτερη κινητική ενέργεια έχει:

α) Το σώμα Σ, β) η ράβδος (ΟΑ), γ) έχουν ίσες κινητικές ενέργειες.

iii) Ελάχιστα πριν την κρούση μεγαλύτερη κατά μέτρο ταχύτητα έχει:

α) Το σώμα Σ,  β) το άκρο Α της ράβδου, γ) Έχουν ταχύτητες ίσου μέτρου.

iv) Αν ακολουθήσει πλαστική κρούση και το σώμα Σ κολλήσει στη ράβδο, τότε αμέσως μετά το στερεό που προκύπτει, θα περιστραφεί με την φορά των δεικτών του ρολογιού ή αντίθετα;

Δίνεται η ροπή αδράνειας της ράβδου ως προς το άκρο της Ο: Ι= 1/3 mℓ².

Απάντηση:

ή

   Μια κρούση ράβδου με υλικό σημείο 

Η ράβδος στο «πλευρό» του δίσκου.

Ο ξύλινος δίσκος του σχήματος μάζας (56/9)kg και ακτίνας R=0,3m, μπορεί να στρέφεται, χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος είναι κάθετος στο επίπεδό του και διέρχεται από το κέντρο του Ο. Καρφώνουμε στο άκρο μιας ακτίνας του δίσκου, το μέσον Μ μιας ομογενούς ράβδου ΑΒ μάζας 12kg και μήκους 0,8m, κατασκευάζοντας έτσι το στερεό s. Αφήνουμε το στερεό s ελεύθερο να κινηθεί από τη θέση, όπου η ράβδος ΑΒ είναι κατακόρυφη, όπως στο σχήμα.

i) Για τη στιγμή αμέσως μόλις αφέθηκε το στερεό να κινηθεί, να βρεθούν:

α) Η γωνιακή επιτάχυνση του s.

β) Οι επιταχύνσεις των άκρων Α και Β της ράβδου.

γ) Οι ρυθμοί μεταβολής της στροφορμής, ως προς τον άξονα περιστροφής στο Ο:

a) του στερεού s,    b) του δίσκου,   c) της ράβδου.

ii) Για τη στιγμή που η ράβδος γίνεται οριζόντια για πρώτη φορά, να βρεθούν:

α) Οι ταχύτητες των άκρων Α και Β της ράβδου.

β) Η στροφορμή της ράβδου ως προς:

a) Τον άξονα περιστροφής στο Ο,  

b) Οριζόντιο άξονα, κάθετο στο επίπεδο του σχήματος, ο οποίος περνά από το μέσον της Μ.

γ) Η κινητική ενέργεια της ράβδου.

Δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του Ι₁= ½ m₁R², η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Μ Ι₂= (1/12)m₂l² και g=10m/s².

Απάντηση:

ή

 Η ράβδος στο «πλευρό» του δίσκου.

Δύναμη στην ταλάντωση.

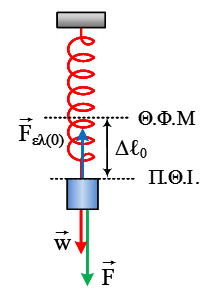Ένα σώμα Σ μάζας m είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k και εκτελεί απλή αρμονική ταλάντωση πλάτους Α₀ = 0,2√3 m. Ο ρυθμός μεταβολής της ορμής έχει μέγιστο μέτρο |dp/dt| = 40√3N κάθε 0,1π s. Κάποια στιγμή που ο ταλαντωτής διέρχεται από την θέση ισορροπίας και κατέρχεται, του ασκούμε με φορά προς τα κάτω σταθερή κατακόρυφη δύναμη F διπλάσια του βάρους.

Α. Να βρεθεί το πλάτος Α₁ και η ενέργεια της ταλάντωσης Ε₁ μετά την άσκηση της δύναμης F.

B. Αν η δύναμη ασκείται για χρονικό διάστημα Δt = π/6 s και μετά καταργείται. Μετά την κατάργηση της δύναμης F:

α. να υπολογισθεί το πλάτος Α₂ της νέας ταλάντωσης

β. να γραφεί η χρονική εξίσωση της απομάκρυνσης της ταλάντωσης (t = 0 η στιγμή εφαρμογής της δύναμης).

γ. Να υπολογίσετε το έργο της F για το χρόνο δράσης της.

Γ. Ποια χρονική στιγμή (η ελάχιστη), έπρεπε να καταργήσουμε την δύναμη F ώστε το πλάτος της ταλάντωσης μετά την κατάργηση της να είναι μέγιστο και ποιο είναι αυτό;

Δίνεται g = 10 m/s², θετική η φορά προς τα πάνω και σε κάθε περίπτωση το σώμα εκτελεί Α.Α.Τ. με D = k.

 

   

 

Δυο διαδοχικές «κρούσεις»

Ένας οριζόντιος δίσκος μάζας Μ=18kg και ακτίνας R=1m μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό κατακόρυφο άξονα z, που περνά από το κέντρο του Ο. Στον άξονα περιστροφής έχουμε περάσει ένα μικρό δακτυλίδι, το οποίο μέσω αβαρούς (τεντωμένου) νήματος μήκους l=0,5m συνδέεται με σώμα Σ₂, το οποίο εμφανίζει με το δίσκο

συντελεστή τριβής μ=0,4 και το οποίο ηρεμεί. Σε μια στιγμή ένα βλήμα το οποίο κινείται οριζόντια με ταχύτητα μέτρου υ₀=200m/s κάθετα  στο νήμα, σφηνώνεται στο σώμα  Σ₂, δημιουργώντας ένα συσσωμάτωμα Σ μάζας m=4kg, το οποίο αποκτά αρχική ταχύτητα υ_Σ=20m/s.

i)  Να υπολογίσετε την απώλεια της μηχανικής ενέργειας η οποία οφείλεται στην κρούση.

ii) Ποια η τάση του νήματος, αμέσως μετά την κρούση;

iii) Κάποια στιγμή η ταχύτητα του συσσωματώματος έχει μέτρο u=10m/s. Για τη στιγμή αυτή να υπολογιστούν:

α) Ο ρυθμός μεταβολής της κινητικής ενέργειας του συσσωματώματος Σ.

β) Ο αντίστοιχος ρυθμός μεταβολής της κινητικής ενέργειας του δίσκου.

iv) Πόση είναι η συνολική μηχανική ενέργεια που εμφανίζεται ως θερμική, εξαιτίας της τριβής μεταξύ του Σ και του δίσκου, μέχρι που να σταματήσει η ολίσθηση του συσσωματώματος πάνω στο δίσκο;

Δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονα z, Ι= ½ ΜR² και g=10m/s².

Απάντηση:

ή

 Δυο διαδοχικές «κρούσεις»