Μια «ιδιόμορφη ζυγαριά».

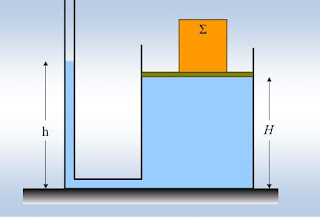
Το δεξιό κυλινδρικό δοχείο του σχήματος κλείνεται με έμβολο, εμβαδού Α=0,6m² και αμελητέου βάρους και περιέχει νερό μέχρι ύψος Η. Το δοχείο συνδέεται με λεπτό κατακόρυφο σωλήνα, όπως στο σχήμα, στον οποίο το νερό φτάνει μέχρι ύψος h.

i)  Για το ύψος h του νερού (χωρίς το σώμα Σ στο έμβολο) στον λεπτό σωλήνα, ισχύει:

α) h < Η,     β) h=Η,      γ) h > Η.

Να δικαιολογήσετε την απάντησή σας.

ii)  Τοποθετούμε πάνω στο έμβολο ένα σώμα Σ, βάρους w=600Ν. Για να μην μετακινηθεί το έμβολο, προτείνεται να προσθέσουμε νερό στον σωλήνα. Να υπολογισθεί το νέο ύψος της στήλης h₁ στο σωλήνα, ώστε να μην μετακινηθεί το έμβολο, παραμένοντας σε ύψος Η..

iii) Να υπολογιστεί το βάρος του νερού που προσθέσαμε στο σωλήνα, για να εξισορροπήσει την τοποθέτηση του σώματος Σ, πάνω στο έμβολο, αν ο σωλήνας έχει διατομή με εμβαδόν S=4cm².

Δίνεται η πυκνότητα του νερού ρ=1.000kg/m³ και g=10m/s².

Απάντηση:

ή

 Μια «ιδιόμορφη ζυγαριά».

Μια «ιδιόμορφη ζυγαριά».

Κάτι σαν Torricelli…

Σε ένα δοχείο με μεγάλη διατομή επιφάνειας που περιέχει νερό τοποθετούμε στρώμα λαδιού ύψους h₁=5m. Σε απόσταση h₂=5m από την επιφάνεια του νερού ανοίγουμε μικρή οπή εμβαδού Α=2cm², όπως φαίνεται στο διπλανό σχήμα. Το νερό εξέρχεται σε κλειστό δοχείο πολύ μεγάλου όγκου που περιέχει αέρα σε πίεση P_αερ=1,4P_atm  και η οποία διατηρείται σταθερή μέσω αισθητήρα ο οποίος μπορεί να καθορίζει κάθε χρονική στιγμή την ποσότητα αέρα στο κλειστό δοχείο.

i) Να βρεθεί η πίεση σε σημείο Γ της διαχωριστικής επιφάνειας λαδιού – νερού.

ii) Να βρεθεί η ταχύτητα και η παροχή με την οποία εξέρχεται το νερό στο κλειστό δοχείο, αν η διατομή της ελεύθερης επιφάνειας του δοχείου είναι πολύ μεγάλη συγκριτικά με την οπή.

iii) Αν η διατομή του δοχείου έχει εμβαδόν Α₁=10cm², να υπολογιστεί ξανά η ταχύτητα εκροής του νερού τη στιγμή t=0 που εισέρχεται στο κλειστό δοχείο που περιέχει αέρα, καθώς και ο ρυθμός με τον οποίο κατεβαίνει η πάνω επιφάνεια του λαδιού.

iv) Να βρείτε που θα σταματήσει η ροή στην περίπτωση του ερωτήματος iii).

v) Αν η διατομή της επιφάνειας του δοχείου είναι πολύ μεγαλύτερη από αυτή της οπής, να βρεθεί ο ρυθμός μεταβολής της ποσότητας mol του αέρα dn/dt που θα πρέπει να εξέρχεται μέσω του αισθητήρα, για να διατηρείται η πίεση στο κλειστό δοχείο σταθερή.

Το αέριο στο κλειστό δοχείο θεωρείται ιδανικό και δεν διαλύεται στο νερό. Ισχύει για αυτό κάθε στιγμή η καταστατική εξίσωση των ιδανικών αερίων PV=nRT, όπου P η πίεση του αερίου, V ο όγκος του, n ο αριθμός των mol, Τ η θερμοκρασία του και R=8,314J/(mol·K)

Η θερμοκρασία του αερίου είναι σταθερή σε όλη τη διεργασία και ίση με Τ=2500/R K.

Δίνεται P_atm=10⁵Pa, η πυκνότητα του νερού ρ_ν=10³kg/m³, η πυκνότητα του λαδιού ρ_λ=800kg/m³ και το μέτρο της επιτάχυνσης της βαρύτητας g=10m/s².

Απάντηση

Ένας αντεστραμμένος σωλήνας

Σε ένα ανοικτό δοχείο με νερό έχουμε αντιστρέψει έναν κατακόρυφο σωλήνα, όπως στο σχήμα (1), όπου το νερό έχει ανέβει κατά α, όσο είναι και το βυθισμένο μέρος του σωλήνα. Το βάρος του σωλήνα θεωρείται αμελητέο.

i)  Για να συγκρατείται στη θέση του ο σωλήνας, πρέπει να του ασκούμε με το χέρι μας:

α) Κατακόρυφη δύναμη προς τα πάνω, όπως η F₁.

β) Κατακόρυφη δύναμη προς τα κάτω, όπως η F₂.

γ) Δεν απαιτείται η άσκηση κάποιας δύναμης.

ii) Ασκώντας κατάλληλη δύναμη στο σωλήνα τον ανεβάζουμε κατά y, φέρνοντάς τον  στη θέση που δείχνει το σχήμα (2). Τότε η στάθμη του νερού στο εσωτερικό του:

α) Θα ανέβει,    β) θα κατέβει,   γ) θα παραμείνει στο ίδιο ύψος α.

Απάντηση:

ή

 Ένας αντεστραμμένος σωλήνας

Ένας αντεστραμμένος σωλήνας

Όταν η πηγή επιταχύνεται...και φαινόμενο doppler.

Τι γίνεται όταν μια ηχητική πηγή επιταχύνεται; Μπορούμε να υπολογίζουμε τη συχνότητα που ακούει ένας ακίνητος παρατηρητής, χρησιμοποιώντας τις γνωστές εξισώσεις που έχουν προκύψει στην περίπτωση που η πηγή κινείται με σταθερή ταχύτητα;
Ας το δούμε:

1. Μια ηχητική πηγή κινείται ευθύγραμμα με σταθερή ταχύτητα υ₀=40m/s παράγοντας ήχο συχνότητας f_s= 600Ηz. Ποια συχνότητα ακούει ένας παρατηρητής που βρίσκεται σε απόσταση d μπροστά από την πηγή; Δίνεται η ταχύτητα του ήχου στον ακίνητο αέρα υ=340m/s.
2. Η παραπάνω πηγή κινείται με σταθερή επιτάχυνση α=4m/s² και σε μια στιγμή t₀=10s, που έχει ταχύτητα υ₀=40m/s, παράγει έναν ήχο. Ποια η συχνότητα του ήχου αυτού, όταν  φτάσει στον παρατηρητή μας Α, στην ίδια απόσταση d;

Απάντηση:
ή
 Όταν η πηγή επιταχύνεται...και φαινόμενο doppler.
  Όταν η πηγή επιταχύνεται...και φαινόμενο doppler.

Λάδι vs Νερό

Στο διπλανό σχήμα απεικονίζονται δύο δοχεία Α και Β.

Το δοχείο Α περιέχει νερό σε μεγάλο ύψος Η_ν και από πάνω του χύνεται στρώμα λαδιού ύψους h=1m. Σε απόσταση y₁=0,9m από την κάτω επιφάνεια του λαδιού ανοίγεται μικρή οπή και το νερό εξέρχεται στην ατμόσφαιρα με ταχύτητα υ₁.

Στο δοχείο Β τοποθετούμε αρχικά το λάδι σε μεγάλο ύψος Η_λ  και κατόπιν νερό μέχρι ύψος h=1m. Η ανάμιξη των υγρών εμποδίζεται από ένα πολύ λεπτό αβαρές έμβολο που τοποθετείται ανάμεσα στο λάδι και το νερό. Σε απόσταση y₂ από την κάτω επιφάνεια του νερού ανοίγεται μικρή οπή και το λάδι εξέρχεται στην ατμόσφαιρα με ταχύτητα υ₂.

i) Για να εξέρχονται με την ίδια ταχύτητα τα δύο ρευστά θα πρέπει η απόσταση y₂ να είναι ίση με:

α) y₂=0,9m                              β) y₂=0,45m                            γ) y₂=0,3m

ii) Για να έχουν ίδιο βεληνεκές η φλέβα του νερού και η φλέβα του λαδιού όταν εξέρχονται από τα δοχεία Α και Β για τα ύψη Η_ν και Η_λ θα πρέπει να ισχύει:

α) Η_ν–Η_λ=0,45m                     β) Η_λ–Η_ν=0,45m                     γ) Η_ν–Η_λ=0,9m

Να επιλέξετε τις απαντήσεις σας.

Να δικαιολογήσετε τις επιλογές σας.

Να θεωρήσετε το νερό και το λάδι ιδανικά ρευστά.

Δίνονται: το μέτρο της επιτάχυνσης της βαρύτητας g=10m/s², η πυκνότητα του νερού ρ_ν=10³kg/m³, η πυκνότητα του λαδιού ρ_λ=0,8·10³kg/m³ και η ατμοσφαιρική πίεση p_atm=10⁵N/m². Η διατομή των δοχείων είναι πολύ μεγαλύτερη της οπής.

Απάντηση

Ένας κύλινδρος σε δοχείο με νερό

Ένα δοχείο κυλινδρικού σχήματος αμελητέας μάζας με εμβαδό βάσης Α=100cm² περιέχει νερό μέχρι ύψους Η=0,5m. Η ελεύθερη επιφάνεια του δοχείου είναι σε επαφή με την ατμόσφαιρα. Από την κάτω πλευρά του δοχείου που εφάπτεται με το δάπεδο επιτρέπεται να μπαίνει ατμοσφαιρικός αέρας.

i) Υπολογίστε την πίεση στον πυθμένα του δοχείου και την δύναμη που δέχεται από το ρευστό.

ii) Βρείτε τη δύναμη επαφής που δέχεται ο πυθμένας από το δάπεδο.

 

Στη συνέχεια βυθίζουμε έναν κύλινδρο μάζας m_κ=0,3kg πυκνότητας ρ_κυλ=750kg/m³ και εμβαδού_κ=20cm² στο νερό, και αυτός επιπλέει βυθισμένος κατά y.

βάσης Α

iii) Nα υπολογίσετε το ύψος h του κυλίνδρου και το ύψος y που βυθίζεται στο νερό.

iv) Βρείτε πόσο ανυψώνεται η στάθμη του νερού στο δοχείο λόγω της βύθισης του κυλίνδρου.

v) Υπολογίστε την νέα τιμή της πίεσης στον πυθμένα του δοχείου και βρείτε πόσο μεταβάλλεται η δύναμη που δέχεται από το ρευστό.

Δίνεται P_atm=10⁵Pa, η πυκνότητα του νερού ρ_ν=10³kg/m³ και το μέτρο της επιτάχυνσης της βαρύτητας g=10m/s².

Απάντηση

Η δύναμη στην τάπα

Ένα δοχείο, κλείνεται με αβαρές έμβολο, το οποίο μπορεί να κινείται χωρίς τριβές, εμβαδού S=0,2m² και περιέχει νερό σε ύψος Η=1m. Στο μέσον της στήλης του νερού, σε ύψος h= ½ Η, υπάρχει ένας μικρός οριζόντιος σωλήνας διατομής Α=1cm², ο οποίος κλείνεται με μια τάπα.

Για να μην φεύγει η τάπα, απαιτείται να της ασκήσουμε οριζόντια δύναμη , όπως στο σχήμα.

i)  Να υπολογιστεί το μέτρο της απαραίτητης δύναμης  για την ισορροπία του εμβόλου.

ii) Τοποθετούμε πάνω στο έμβολο ένα βαρύ σώμα Σ, με αποτέλεσμα να απαιτείται να αυξήσουμε την ασκούμενη δύναμη στο έμβολο στην τιμή F₂=0,6Ν. Να υπολογιστεί το βάρος του σώματος Σ.

iii) Αφαιρούμε το σώμα Σ και με τη βοήθεια ενός νήματος που έχουμε δέσει στο έμβολο, του ασκούμε μια κατακόρυφη δύναμη , όπως στο τρίτο σχήμα, μέτρου F=200Ν.

α) Να υπολογιστεί το μέτρο της  δύναμης F₃ που πρέπει να ασκούμε στην τάπα για την ισορροπία της.

β) Πόση δύναμη ασκεί το νερό στον πυθμένα του δοχείου και πόση στο έμβολο;

Δίνεται η ατμοσφαιρική πίεση p_ατ=10⁵Ρa, η πυκνότητα του νερού ρ=1.000kg/m³ και g=10m/s². Σημειώνεται ακόμη ότι, λέγοντας αβαρές έμβολο, εννοούμε ένα έμβολο το οποίο έχει βάρος, απλά το θεωρούμε αμελητέο.

Απάντηση:

ή

 Η δύναμη στην τάπα

Η δύναμη στην τάπα