Διαγώνισμα στερεό 2022

Μία λεπτή ομογενής ράβδος (ρ₁) μήκους ℓ = (ΑΓ) = 4 m και βάρους w₁ = 10 N, είναι αρθρωμένη στο σημείο Α και ισορροπεί οριζόντια ακουμπώντας πάνω σε μία ομογενή σφαίρα ακτίνας R = 20 cm βάρους w₂ = 20 N. Το σημείο επαφής σφαίρας ράβδου απέχει απόσταση ℓ/4 από το σημείο Α. Η σφαίρα βρίσκεται πάνω σε άλλη ομογενή ράβδο μήκους d και ακουμπά ακριβώς στο μέσο της, όπως φαίνεται στο διπλανό σχήμα.

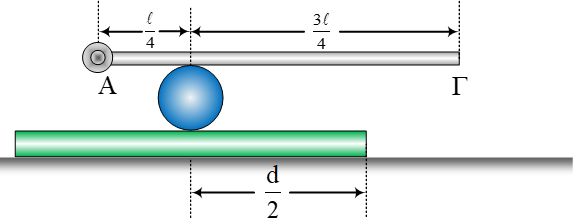
α. Να βρείτε τη δύναμη που δέχεται η κάτω ράβδος (ρ₂) από τη σφαίρα.

- Κάποια στιγμή δίνουμε στην κάτω ράβδο (ρ₂) ταχύτητα μέτρου υ και η σφαίρα δεν ολισθαίνει με καμία ράβδο.

β. Να βρείτε το μήκος d της ράβδου ρ₂, αν η σφαίρα χάνει ταυτόχρονα την επαφή της και με τις δύο ράβδους.

γ. Να βρείτε τον αριθμό των περιστροφών που έχει κάνει η σφαίρα ως τότε.

- Με την ίδια ράβδο (ρ₂) και τη σφαίρα φτιάχνουμε ένα κεκλιμένο επίπεδο τέτοιο ώστε μόλις αφήσουμε την σφαίρα να κυλίσει (χωρίς ολίσθηση) πάνω σε αυτό να αποκτά επιτάχυνση μέτρου α_cm = 5 m/s².

δ. Να βρείτε ποια χρονική στιγμή (μετά την εκκίνηση) το σημείο Σ της σφαίρας που βρίσκεται σε μία ακτίνα παράλληλη με το κεκλιμένο επίπεδο και απέχει r = 5 cm από την περιφέρεια θα αποκτήσει ταχύτητα μέτρου υ = 2,5 m/s.

 

Η συνέχεια εδώ.