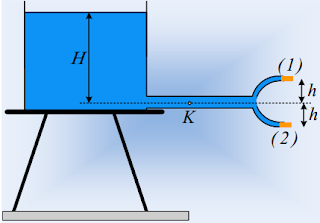
Ένα μεγάλο ντεπόζιτο περιέχει
νερό και στο κάτω μέρος του συνδέεται οριζόντιος σωλήνας διατομής Α, ο οποίος
καταλήγει σε δυο μικρότερους σωλήνες (1) και (2), όπως στο σχήμα, με διατομές Α1=Α2=
½ Α . Το σημείο Κ, στον οριζόντιο σωλήνα, απέχει κατακόρυφη απόσταση Η από την
ελεύθερη επιφάνεια του νερού, ενώ οι μικρότεροι σωλήνες στην έξοδο φράσσονται
με τάπες, οι οποίες απέχουν κατακόρυφες αποστάσεις h, από το Κ.
i) Η πίεση στο σημείο Κ έχει τιμή pΚ, όπου:
α) pΚ=pατμ, β) pΚ=pατμ+ρgΗ, γ) pΚ=pατμ+ρgh, δ) pΚ=ρgΗ
όπου pατμ η ατμοσφαιρική πίεση, ρ η
πυκνότητα του νερού και g η επιτάχυνση της βαρύτητας.
ii) Αν ανοίξουμε την τάπα (1) και αποκατασταθεί μια
μόνιμη στρωτή ροή, για την πίεση p1 στο Κ ισχύει:
α) p1 < pΚ, β) p1 = pΚ, γ) p1 > pΚ.
iii) Αν ανοίξουμε ταυτόχρονα και τις δύο τάπες, μόλις
αποκατασταθεί μια μόνιμη στρωτή ροή, για την πίεση p2 στο Κ ισχύει:
α) p2 < p1, β) p2 = p1, γ) p2 > p1.
Θεωρούμε το νερό ιδανικό ρευστό
και ότι κατά τις παραπάνω ροές, η επιφάνεια του νερού στο ντεπόζιτο παραμένει
σταθερή.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.