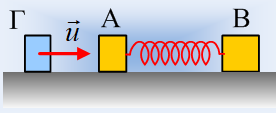
Δυο σώματα Α και Β ηρεμούν σε οριζόντιο επίπεδο με το
οποίο εμφανίζουν συντελεστές τριβής μ=μs=0,4, δεμένα στα άκρα ιδανικού
ελατηρίου σταθεράς k=260Ν/m, το οποίο έχει το φυσικό μήκος του.
Ένα τρίτο σώμα Γ, μάζας m=0,5kg κινείται κατά μήκος του
άξονα του ελατηρίου και συγκρούεται κεντρικά και ελαστικά με το σώμα Α, έχοντας
τη στιγμή της κρούσης ταχύτητα u. Το σώμα Α, μάζας m1=1kg, αποκτά
ταχύτητα υο=4m/s αμέσως μετά την κρούση.
i)
Να υπολογιστεί η ταχύτητα u του σώματος Γ, πριν την κρούση.
ii)
Να υπολογιστούν οι ρυθμοί μεταβολής της ορμής και της κινητικής ενέργειας του
σώματος Α, αμέσως μετά την κρούση.
Αν το σώμα Β ξεκινά την ολίσθησή του, μόλις το σώμα Α
διανύσει απόσταση x=0,2m:
iii)
Να υπολογιστεί η μάζα του σώματος Β.
iv)
Να υπολογιστούν οι ρυθμοί μεταβολής της ορμής και της κινητικής ενέργειας των
σωμάτων Α και Β, ελάχιστα πριν αρχίσει η ολίσθηση του Β σώματος.
Δίνεται g=10m/s2.
ή