ΩΘΗΣΗ ΚΑΙ ….ΑΠΟ ΤΟ ΖΕΝΙΘ ΣΤΟ ΝΑΔΙΡ
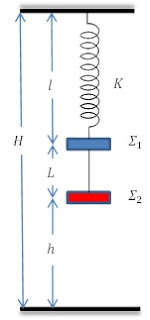
Ένα σώμα Σ1 μάζας m1=1kg είναι στερεωμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου φυσικού μήκους l0=0,9m και σταθεράς σκληρότητας K, το πάνω άκρο του οποίου είναι στερεωμένο σε οροφή. Δεύτερο σώμα Σ2 μάζας m2=3kg είναι δεμένο με αβαρές και μη εκτατό νήμα μήκους L με το σώμα Σ1. Το σύστημα των δύο σωμάτων ισορροπεί ακίνητο με το ελατήριο να έχει μήκος l=1,3 m και το σώμα Σ2 να βρίσκεται σε ύψος h από το δάπεδο.
A. Τη χρονική στιγμή t=0 εκτοξεύουμε με κατάλληλη αρχική ταχύτητα το σώμα Σ1 κατακόρυφα προς τα πάνω, ώστε το νήμα να παραμένει οριακά τεντωμένο και να μην χαλαρώνει κατά την κίνηση του
συστήματος των δύο σωμάτων.
A1 . Να δείξετε ότι το σύστημα των δύο σωμάτων εκτελεί απλή αρμονική ταλάντωση και να υπολογίσετε το ρυθμό μεταβολής της φάσης της ταλάντωσης. Να θεωρήσετε ως θετική για την ταλάντωση τη φορά της συσπείρωσης του ελατηρίου και ως θέση ισορροπίας της ταλάντωσης των δύο σωμάτων η θέση του σώματος Σ1 .
A2 . Να υπολογίσετε την κατάλληλη αρχική ταχύτητα εκτόξευσης του σώματος Σ1 καθώς και τη μέση δύναμη που ώθησε το σώμα αν αυτή ασκήθηκε για αμελητέο χρονικό διάστημα Δt=5⋅10-2 sec (λάκτισμα) ώστε η ταλάντωση να ξεκινά από τη θέση ισορροπίας της.
B. Αν το νήμα φθείρεται κατά τη διάρκεια του λακτίσματος σε μεγάλο ποσοστό και σπάει όταν η τάση του νήματος λαμβάνει τη μέγιστη τιμή της για πρώτη φορά στη διάρκεια της απλής αρμονικής ταλάντωσης του συστήματος :
B1 . Να υπολογίσετε το όριο θραύσης του νήματος και τη χρονική στιγμή της θραύσης στη διάρκεια της απλής αρμονικής ταλάντωσης.
Αν για την νέα απλή αρμονική ταλάντωση του σώματος Σ1 η χρονική στιγμή της θραύσης του νήματος είναι η στιγμή t'=0 τότε :
B2 . Να υπολογίσετε το μήκος L του νήματος και το ύψος H οροφής – δαπέδου, αν τη στιγμή που ο ρυθμός μεταβολής της κινητικής ενέργειας του σώματος Σ1 μηδενίζεται για τρίτη φορά μετά την έναρξη της ταλάντωσής του, το σώμα Σ2 μόλις φθάνει στο δάπεδο και τα σώματα Σ1 και Σ2 απέχουν τότε απόσταση d=2m.
Δίνεται : η επιτάχυνση της βαρύτητας g=10m/s2 και ότι π2=10
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.