Στο σχήμα μια δεξαμενή περιέχει
νερό σε ύψος Η=1,25m και κοντά στον πυθμένα της συνδέεται οριζόντιος σωλήνας,
διατομής 0,4cm2, το άκρο του οποίου έχουμε κλείσει με μια τάπα. Στον
σωλήνα αυτόν, έχει προσαρμοσθεί ένας δεύτερος λεπτός κατακόρυφος σωλήνας, ύψους
Η, κλειστός στο άνω άκρο του, εντός του οποίου το νερό έχει ανέβει κατά h=1m.
i) Πόση δύναμη δέχεται η τάπα από το νερό και ποια η
πίεση του εγκλωβισμένου αέρα στον κατακόρυφο σωλήνα;
ii) Σε μια στιγμή βγάζουμε την τάπα και το νερό εκρέει
από το άκρο Β του σωλήνα. Να βρεθεί η παροχή του σωλήνα.
iii) Να βρεθεί το ύψος που ανέρχεται το νερό στο
κατακόρυφο σωλήνα, στη διάρκεια της παραπάνω ροής.
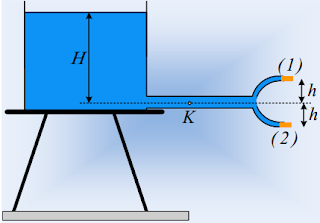
iv) Λυγίζουμε τον σωλήνα, ώστε να πάρει τη μορφή του
σχήματος, όπου d=55cm. Ποιο το ύψος του νερού στον κατακόρυφο σωλήνα;
Θεωρούμε πολύ μεγάλη την
ελεύθερη επιφάνεια του νερού στην δεξαμενή, το νερό ιδανικό ρευστό με πυκνότητα
ρ=1.000kg/m3 και τη ροή μόνιμη (για το χρονικό διάστημα, που πραγματοποιούμε
το πείραμα). Δίνονται ακόμη g=10m/s2 και pατμ=105Ρa, ενώ η θερμοκρασία του εγκλωβισμένου αέρα παραμένει
σταθερή. Υπενθυμίζεται δε και ο νόμος του Boyle!!! Για μια ποσότητα αερίου σε σταθερή θερμοκρασία
pV=σταθ.