Δύο αγωγοί και ο νόμος του Ampère

  

Κάθετα στο επίπεδο της σελίδας έχουμε δυο ευθύγραμμους αγωγούς, που τέμνουν το επίπεδο στα σημεία Α και Γ, οι οποίοι διαρρέονται από ρεύματα με εντάσεις Ι₁ και Ι₂, αντίστοιχα. Σε ένα σημείο Δ, πάνω στο τμήμα ΑΓ, ο πρώτος αγωγός δημιουργεί μαγνητικό πεδίο έντασης Β₁=2∙10^-5Τ, ενώ η συνολική ένταση του μαγνητικού πεδίου, εξαιτίας και των δύο αγωγών έχει μέτρο Β=10^-5Τ.

i)  Ποια η φορά της έντασης Ι₂ που διαρρέει τον δεύτερο αγωγό στο Γ;

ii) Στο σχήμα δίνονται δύο στοιχειώδη τμήματα με αρχή το σημείο Δ, το Δl₁, με κατεύθυνση προς το Γ και το Δl₂ κάθετο στην ΑΓ, όπως στο σχήμα, όπου Δl₁=Δl₂=0,2cm. Να υπολογίσετε για τα τμήματα αυτά το γινόμενο Β_i∙Δl_i∙συνθ_i, όπου θ_i η εκάστοτε γωνία μεταξύ της έντασης του πεδίου Β_i και του Δl_i.

iii)  Με κέντρο το μέσον Κ του τμήματος ΑΓ, σχεδιάζουμε το ημικύκλιο ΔΜΕ. Κατά μήκος του ημικυκλίου αυτού, κινούμενοι από το Δ προς το Ε, ισχύει για το άθροισμα: 

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Δύο αγωγοί και ο νόμος του Ampère

Δύο αγωγοί και ο νόμος του Ampère

Μαγνητικό πεδίο δύο αγωγών

 

Στο επίπεδο της σελίδας δίνεται ένα ορθογώνιο τρίγωνο ΑΒΓ (Α=90°). Δυο ευθύγραμμοι αγωγοί μεγάλου μήκους, είναι κάθετοι στο επίπεδο του τριγώνου και διαρρέονται από ρεύματα με εντάσεις Ι₁ και Ι₂. Ο πρώτος αγωγός περνά από την κορυφή Β του τριγώνου, και το ρεύμα έχει φορά προς τα μέσα, όπως στο σχήμα, ενώ ο δεύτερος αγωγός περνά από την κορυφή Γ.

i)  Να σχεδιάσετε το διάνυσμα της έντασης του μαγνητικού πεδίου, που δημιουργεί ο πρώτος αγωγός, στην κορυφή Α του τριγώνου.

ii)  Αν η συνολική ένταση του μαγνητικού πεδίου στο Α, που οφείλεται και στους δύο αγωγούς, έχει την διεύθυνση της  διαμέσου ΑΜ του τριγώνου, ο δεύτερος αγωγός στο Γ, διαρρέεται από ρεύμα της ίδιας φοράς ή αντίθετης φοράς από τον πρώτο αγωγό;

iii) Για τις εντάσεις των ρευμάτων που διαρρέουν τους δύο αγωγούς,  ισχύει:

α) Ι₁ < Ι₂,          β) Ι₁ = Ι₂,        γ) Ι₁ > Ι₂.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Μαγνητικό πεδίο δύο αγωγών

Μαγνητικό πεδίο δύο αγωγών

Τρία τμήματα αγωγού και το μαγνητικό τους πεδίο

 

Ένα αγωγός x΄ΑΓx, βρίσκεται στο επίπεδο της σελίδας και αποτελείται από δύο τμήματα x΄Α και Γx που είναι ευθύγραμμα πολύ μεγάλου μήκους και το τμήμα ΑΓ το οποίο είναι ένα τεταρτοκύκλιο κέντρου Ο και ακτίνας r=0,1m. Ο αγωγός διαρρέεται από ρεύμα έντασης Ι=2Α με φορά από το x΄ προς το x, όπως στο σχήμα.

i) Να αποδείξετε ότι το τμήμα x΄Α δεν δημιουργεί μαγνητικό πεδίο στο σημείο Ο, το οποίο βρίσκεται στην προέκτασή του.

ii) Να βρεθεί η ένταση του μαγνητικού πεδίου στο σημείο Ο, το οποίο οφείλεται στο τεταρτοκύκλιο ΑΓ.

iii) Να υπολογιστεί η ένταση του μαγνητικού πεδίου στο σημείο Ο, που οφείλεται σε όλο τον αγωγό x΄ΑΓx.

Δίνεται μ_ο=4π×10^-7Τm/Α.

Απάντηση:

ή

 Τρία τμήματα αγωγού και το μαγνητικό τους πεδίο

 Τρία τμήματα αγωγού και το μαγνητικό τους πεδίο

Δύο αγωγοί στο ίδιο επίπεδο

 

Στο επίπεδο της σελίδας βρίσκονται δύο αγωγοί. Ένας ευθύγραμμος, πολύ μεγάλου μήκους, ο οποίος διαρρέεται από ρεύμα έντασης Ι₁, με φορά όπως στο σχήμα και ένας κυκλικός ο οποίος έχει ακτίνα R και διαρρέεται από ρεύμα έντασης Ι₂. Η απόσταση του κέντρου Κ του κυκλικού αγωγού, από τον ευθύγραμμο αγωγό είναι d=2R. Στο σχήμα βλέπετε ένα στοιχειώδες τμήμα Δl₁ του ευθύγραμμου αγωγού, στο σημείο Α, το οποίο δημιουργεί στο Κ, μια στοιχειώδη ένταση μαγνητικού πεδίου ΔΒ₁, ενώ η απόστασή του (ΑΚ)=r, σχηματίζει με τον αγωγό γωνία θ=30°.  Ένα αντίστοιχο στοιχειώδες τμήμα Δl₂=Δl₁=Δl του κυκλικού  αγωγού στο σημείο Γ, δημιουργεί στο κέντρο Κ, ένταση μαγνητικού πεδίου ΔΒ₂. Αν η συνολική ένταση του μαγνητικού πεδίου που δημιουργούν τα δύο παραπάνω στοιχειώδη τμήματα στο κέντρο Κ είναι μηδενική:

i)  Να βρείτε την φορά του ρεύματος που διαρρέει τον κυκλικό αγωγό.

ii) Για τις εντάσεις των δύο ρευμάτων, που διαρρέουν τους αγωγούς ισχύει:

α) Ι₁ < 16 Ι₂,       β) Ι₁ =16 Ι₂,    γ) Ι₁ >16 Ι₂.

iii) Αν Β₁ το μέτρο της έντασης του μαγνητικού πεδίου στο κέντρο Κ, η οποία οφείλεται στον ευθύγραμμο αγωγό και Β₂ το αντίστοιχο μέτρο της έντασης εξαιτίας του κυκλικού αγωγού, ισχύει:

α) Β₁ < (16/π) Β₂,       β) Β₁ = (16/π) Β₂,       γ) Β₁ > (16/π) Β₂.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Δύο αγωγοί στο ίδιο επίπεδο

 Δύο αγωγοί στο ίδιο επίπεδο

Δύο κύματα διαδίδονται αντίθετα

 Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδονται αντίθετα δύο όμοια εγκάρσια αρμονικά κύματα (1) και (2) και τη στιγμή t₀=0, φτάνουν στα σημεία Ο και Ρ, όπως στο σχήμα, όπου (ΟΡ)=5m. Θεωρώντας το σημείο Ο, ως αρχή ενός προσανατολισμένου συστήματος αξόνων (x,y)=(0,0), η εξίσωση του πρώτου κύματος, το οποίο διαδίδεται προς την θετική κατεύθυνση είναι της μορφής: 

i)  Να βρεθεί η εξίσωση του δεύτερου κύματος, το οποίο διαδίδεται προς τα αριστερά, στο ίδιο σύστημα αξόνων.

ii)  Να βρεθεί η εξίσωση του στάσιμου κύματος που θα προκύψει από την συμβολή των δύο παραπάνω κυμάτων.

iii) Αφού πρώτα βρείτε τη συνάρτηση y=f(x), για την απομάκρυνση κάθε σημείου του μέσου, μεταξύ Ο και Ρ, σε συνάρτηση με την θέση του, να σχεδιάσετε τη μορφή του μέσου, τις χρονικές στιγμές:

α) t_α=1,5s,   β)  t_β=3s  και  t_γ=3,5s.

iv) Να βρεθεί η ταχύτητα ταλάντωσης ενός  σημείου Β, στη θέση x=1,75m τις παραπάνω χρονικές στιγμές.

Απάντηση:

ή

 Δύο κύματα διαδίδονται αντίθετα

Δύο κύματα διαδίδονται αντίθετα

Μελετώντας ένα στάσιμο κύμα

 

Πάνω σε μια ελαστική χορδή με σταθερά τα δυο της άκρα Κ και Λ, έχει σχηματισθεί ένα στάσιμο κύμα και τη στιγμή t₀=0 η μορφή της είναι αυτή του σχήματος, όπου το σημείο Β, το οποίο απέχει οριζόντια απόσταση 0,25m από το άκρο Κ έχει απομάκρυνση y_Β=0,2m (τα θετικά προς τα πάνω) και μηδενική ταχύτητα ταλάντωσης. Στο διάγραμμα δίνεται η φάση της απομάκρυνσης του σημείου Β, σε  συνάρτηση με το χρόνο. Δίνεται ότι η ταχύτητα διάδοσης ενός τρέχοντος κύματος κατά μήκος της  χορδής αυτής είναι υ=12m/s, ενώ ένα σημείο Ο μεταξύ Κ και Δ, απέχει οριζόντια 0,75m από το Κ.

i)   Να υπολογιστεί το μήκος (ΚΛ) της χορδής, τη στιγμή που όλα τα σημεία της περνούν από τη θέση ισορροπίας τους.

ii)  Να γίνει η αντίστοιχη γραφική παράσταση της φάσης φ=f(t) για τα σημεία Ο και Γ.

iii) Για να μπορέσουμε να γράψουμε την εξίσωση του στάσιμου κύματος, θεωρούμε ως αρχή του άξονα x τη θέση του σημείου Ο, με την προς τα δεξιά κατεύθυνση ως θετική.

α) Να βρεθεί το μέγιστο πλάτος του στάσιμου κύματος.

β) Να γράψετε την εξίσωση του στάσιμου κύματος.

Απάντηση:

ή

Μελετώντας ένα στάσιμο κύμα

Μελετώντας ένα στάσιμο κύμα

Δύο όμοια στιγμιότυπα

 

Στο σχήμα βλέπετε στιγμιότυπα δύο κυματομορφών, μιας περιοχής δύο όμοιων γραμμικών ελαστικών μέσων (δύο όμοιων χορδών) τα οποία ελήφθησαν μια χρονική στιγμή t₁. Η μορφή (Ι) δείχνει τμήμα της πρώτης χορδής όταν πάνω της διαδίδεται ένα τρέχον κύμα, ενώ η (ΙΙ), όταν στην δεύτερη χορδή έχει σχηματισθεί ένα στάσιμο κύμα. Στο σχήμα επίσης φαίνεται η ταχύτητα ταλάντωσης του σημείου Β της πρώτης χορδής. Δίνεται ακόμη ότι το πλάτος του τρέχοντος κύματος Α, είναι ίσο με το μέγιστο πλάτος του στάσιμου κύματος Α, ενώ τα σημεία Γ και Λ έχουν ίσες απομακρύνσεις y=+A.

i)  Να σχεδιάσετε πάνω στο σχήμα τις ταχύτητες όλων των σημείων που έχουν σημειωθεί.

ii) Μεγαλύτερη ταχύτητα στην διάρκεια μιας ταλάντωσης θα αποκτήσει:

α) το σημείο Γ,   β) το σημείο Λ,  γ) τα δύο σημεία θα αποκτήσουν ταχύτητες με ίσα πλάτη.

iii) Αν Δφ₁ η διαφορά φάσης μεταξύ των σημείων Γ και Ε και Δφ₂ η διαφορά φάσης μεταξύ των σημείων Λ και Ν, ισχύει:

α) Δφ₁ < Δφ₂,        β) Δφ₁ = Δφ₂,         γ) Δφ₁ > Δφ₂.

iv) Να σχεδιάσετε αντίστοιχο σχήμα που να εμφανίζονται ξανά τα δύο στιγμιότυπα (για τις ίδιες περιοχές), μετά από χρόνο Δt= 1/8 Τ, όπου Τ η περίοδος του τρέχοντος κύματος.

Απάντηση:

ή

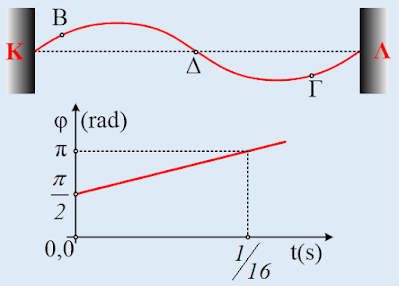
Δύο όμοια στιγμιότυπα

Δύο όμοια στιγμιότυπα

Μια ανάκλαση κύματος σε τοίχο

  Κατά μήκος ενός ελαστικού νήματος, το ένα άκρο του οποίου είναι δεμένο σε τοίχο, διαδίδεται ένας παλμός, όπως στο σχήμα, τον οποίο προσεγγίζουμε με ημιτονοειδή καμπύλη.

i)  Ποιο από τα παρακάτω σχήματα δείχνει τη μορφή του νήματος, τη στιγμή που το σημείο Γ φτάνει στον τοίχο;

ii) Ποιο από τα παρακάτω σχήματα δείχνει τη μορφή του νήματος, τη στιγμή που το σημείο B φτάνει στον τοίχο;

 

ii)  Ποιο από τα παρακάτω σχήματα δείχνει τη μορφή του νήματος, τη στιγμή που το σημείο Α φτάνει στον τοίχο;

 

Να δώσετε σύντομες δικαιολογήσεις για τις επιλογές σας.

Απάντηση:

ή

 Μια ανάκλαση κύματος σε τοίχο

Μια ανάκλαση κύματος σε τοίχο

Μια συμβολή δύο ημιτονοειδών παλμών

 Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδονται αντίθετα δυο ημιτονοειδείς παλμοί με το ίδιο πλάτος Α και το ίδιο μήκος κύματος λ. Σε μια στιγμή t₀=0 οι παλμοί φτάνουν στα σημεία Γ και Δ, όπου  (ΓΔ)=λ/2, όπως στο σχήμα. 

 

Τη στιγμή αυτή το σημείο Β έχει ταχύτητα ταλάντωσης μέτρου u.

i)  Να σχεδιάσετε πάνω στο σχήμα τις ταχύτητες ταλάντωσης των σημείων Β και Γ και Δ. Ποια τα μέτρα των ταχυτήτων ταλάντωσης των σημείων Γ και Δ;

ii)   Αν οι δύο παλμοί συναντηθούν στο σημείο Μ τη στιγμή t₁:

α) Να σχεδιάσετε τη μορφή του μέσου τη στιγμή αυτή.

β)  Ποιες οι ταχύτητες ταλάντωσης των σημείων Β, Γ, Μ και Δ  την στιγμή αυτή;

iii)  Σε μια στιγμή το 1^ο κύμα φτάνει στο σημείο Δ. Για τη στιγμή αυτή:

α) Να σχεδιάσετε τη μορφή του μέσου.

β)  Ποιες οι ταχύτητες ταλάντωσης των σημείων Β, Γ, Μ και Δ;

Απάντηση:

ή

 Μια συμβολή δύο ημιτονοειδών παλμών

 Μια συμβολή δύο ημιτονοειδών παλμών

Δυο εξισώσεις δύο αρμονικών κυμάτων

Κατά μήκος δύο γραμμικών ελαστικών μέσων και από αριστερά προς τα δεξιά (θετική κατεύθυνση) διαδίδονται δύο αρμονικά κύματα με το ίδιο πλάτος Α και την ίδια ταχύτητα διάδοσης u. Τη στιγμή t₀=0, το πρώτο κύμα (Ι) φτάνει στο σημείο Κ, ενώ το δεύτερο (ΙΙ) στο σημείο Ο, στη θέση x=0, όπως παρουσιάζονται στο παραπάνω σχήμα.

i) Να αποδείξετε ότι η εξίσωση κύματος y=f(x,t) για το πρώτο κύμα παίρνει τη μορφή:

ii) Ποια η εξίσωση της απομάκρυνσης y=f(t) του σημείου Ο, στη θέση x=0, λόγω του κύματος (Ι) και ποια η αντίστοιχη εξίσωση λόγω του κύματος (ΙΙ);

iii) Να αποδειχθεί ότι και το δεύτερο κύμα (ΙΙ), έχει την ίδια εξίσωση κύματος (1),  με το κύμα (Ι).

iv) Να σχεδιάσετε ένα ποιοτικό διάγραμμα για το στιγμιότυπο του κύματος (ΙΙ), τη στιγμή που φτάνει στο σημείο Κ.

Απάντηση:

ή

 Δυο εξισώσεις δύο αρμονικών κυμάτων 

 Δυο εξισώσεις δύο αρμονικών κυμάτων 

Από ένα στιγμιότυπο κύματος

 Κατά μήκος ενός γραμμικού ελαστικού μέσου και από αριστερά προς τα δεξιά (θετική κατεύθυνση) διαδίδεται ένα εγκάρσιο αρμονικό κύμα, το οποίο τη στιγμή t₀=0 φτάνει στην αρχή Ο, ενός συστήματος αξόνων x,y. Στο σχήμα βλέπουμε ένα στιγμιότυπο του κύματος τη χρονική στιγμή t₁=0,9s, όπου το σημείο Ο βρίσκεται στην μέγιστη θετική απομάκρυνσή του y_Ο=+0,2m.

i) Να βρεθούν το μήκος κύματος, η περίοδος και η ταχύτητα του κύματος.

ii) Ποια η εξίσωση του κύματος;

iii) Ένα σημείο Κ βρίσκεται στη θέση x_K=4/3m.

α) Να βρεθεί η απομάκρυνση, η ταχύτητα και η επιτάχυνση του σημείου Κ, τη στιγμή t₁.

β) Να βρεθεί η απομάκρυνση το σημείου Κ, από τη θέση ισορροπίας του, τις χρονικές στιγμές:

a)  t₂=0,6s   και b)   t₃=29/30s.

Απάντηση:

ή

  Από ένα στιγμιότυπο κύματος

Από ένα στιγμιότυπο κύματος