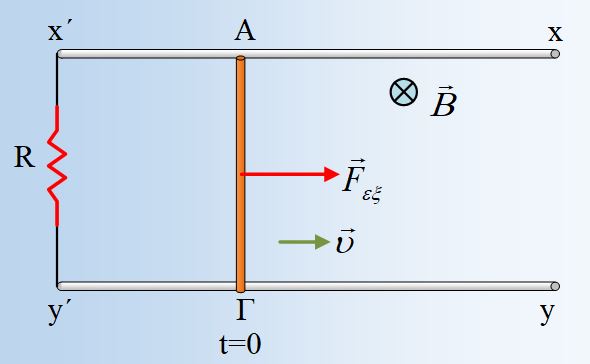
Δυο οριζόντιοι παράλληλοι αγωγοί x΄x και y΄y, δεν εμφανίζουν αντίσταση, ενώ απέχουν απόσταση d=1m. Στα άκρα τους x΄, y΄ συνδέεται ένας αντιστάτης με αντίσταση R=3Ω. Ένας ευθύγραμμος ομογενής αγωγός ΑΓ, μήκους l=1m, μάζας m=0,5kg και αντίστασης R1=2Ω, κινείται σε επαφή με τους αγωγούς x΄x και y΄y, με τους οποίους δεν παρουσιάζει τριβές, με σταθερή ταχύτητα υ=2m/s, με την επίδραση κατάλληλης σταθερής εξωτερικής δύναμης Fεξ, παράλληλης στην x΄x. Το όλο σύστημα βρίσκεται μέσα σε ένα ομογενές κατακόρυφο μαγνητικό πεδίο έντασης Β=0,5Τ, όπως στο σχήμα, ενώ τη στιγμή t=0 η απόσταση του αγωγού ΑΓ από τα άκρα x΄y΄ είναι d1=(x΄Α)=0,8m. Θεωρώντας την κάθετη στην επιφάνεια x΄ΑΓy΄ να έχει την κατεύθυνση της έντασης του μαγνητικού πεδίου, να βρεθούν:
i) Η μαγνητική ροή που διέρχεται από την επιφάνεια ΑΓy΄x΄, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση μέχρι τη χρονική στιγμή t1 =2s.
ii) Η ΗΕΔ από επαγωγή που αναπτύσσεται στον αγωγό ΑΓ, καθώς και η ένταση του ρεύματος που τον διαρρέει.
iii) Να βρεθεί το μέτρο της δύναμης Laplace, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση, η οποία ασκείται:
α) στον αγωγό ΑΓ.
β) στον αγωγό x΄x
iv) Αν η εξωτερική δύναμη καταργηθεί τη χρονική στιγμή t1, να υπολογιστούν τα ολικά έργα των παραπάνω δυνάμεων Laplace οι οποίες ασκούνται στους αγωγούς ΑΓ και x΄x, μέχρι να σταματήσει η κίνηση του ΑΓ.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.