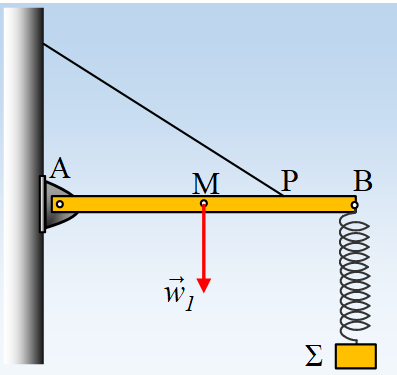
Η ομογενής δοκός ΑΒ μάζας Μ, μπορεί να στρέφεται γύρω από άρθρωση στο άκρο της Α και ισορροπεί οριζόντια, όταν στο άκρο της Β κρέμεται μέσω ελατηρίου ένα σώμα Σ, μάζας m, ενώ συγκρατείται μέσω νήματος, το οποίο έχουμε δέσει στο σημείο Ρ, όπως στο σχήμα. Κάποια στιγμή θέτουμε το Σ σε κατακόρυφη ταλάντωση με πλάτος Α=2mg/k.
i) Θεωρώντας την προς τα πάνω κατεύθυνση ως θετική, η αλγεβρική τιμή της δύναμης του ελατηρίου η οποία ασκείται στο σώμα Σ, σε συνάρτηση της απομάκρυνσης y, δίνεται από την σχέση:
α) Fελ=-mg+ky, β) Fελ=mg-ky, γ) Fελ=-mg-ky
ii) Αν κατά την παραπάνω ταλάντωση οριακά εξασφαλίζεται η ισορροπία της ράβδου, χωρίς να λυγίζει το νήμα, τότε για τις μάζες Μ και m ισχύει:
α) Μ=m, β) Μ=2m, γ) Μ=3m, δ) Μ=4m.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.