Αβαρές νήμα και αβαρής ράβδος

ή Μεταφορική και Στροφική κίνηση

Μια ομογενής λεπτή ράβδος ΑΒ μήκους ℓ=2m συγκρατείται σε κατακόρυφη θέση, δεμένη στο άκρο οριζόντιου νήματος, μήκους επίσης ℓ, στο μέσον της Μ. Το άλλο άκρο του νήματος στερεώνεται σε σταθερό σημείο Ο, αμέσως μόλις αφεθεί ελεύθερη να κινηθεί.

i)  Αφήνουμε τη ράβδο να κινηθεί. Να βρεθούν οι επιταχύνσεις του μέσου της Μ και του άκρου Β της ράβδου.

ii)  Ποια θα είναι η αντίστοιχη απάντηση στο παραπάνω ερώτημα, αν αντικαταστήσουμε το αβαρές νήμα, με αβαρή ράβδο ΟΜ;

Δίνεται g=10m/s², καθώς και η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα ο οποίος περνά από το μέσον της Ι_cm=mℓ²/12.

Απάντηση:

ή

 Αβαρές νήμα και αβαρής ράβδος

 Αβαρές νήμα και αβαρής ράβδος

Τα έργα των δυνάμεων και η κινητική ενέργεια

Σε λείο οριζόντιο επίπεδο ηρεμεί ένας ομογενής  οριζόντιος δίσκος μάζας 20kg και ακτίνας 0,5m. . Τυλίγουμε γύρω του ένα αβαρές και μη εκτατό νήμα, στο άκρο Α του οποίου τη στιγμή t=0 ασκούμε, μια οριζόντια δύναμη μέτρου F₂=10Ν, ενώ ταυτόχρονα στο κέντρο του Ο ασκούμε μια αντιπαράλληλη δύναμη μέτρου F₁=16Ν, όπως στο σχήμα (σε κάτοψη).  Διατυπώνονται δύο προτάσεις:

Α)  Το έργο της δύναμης F₁ μετράει την ενέργεια που μεταφέρεται στο δίσκο και εμφανίζεται με τη μορφή της «μεταφορικής» κινητικής ενέργειας.

Β) Το έργο της δύναμης F₂ μπορεί να υπολογιστεί και ως έργο της ροπής F₂.

Για τον έλεγχο της ορθότητας των παραπάνω προτάσεων, ας δούμε τα παρακάτω ερωτήματα:

Για την κίνηση από τη στιγμή t=0 μέχρι τη στιγμή t₁=10s, να υπολογιστούν:

i)  Η επιτάχυνση του κέντρου μάζας Ο του δίσκου, καθώς και η γωνιακή του επιτάχυνση.

ii) Το έργο της δύναμης F₁ και η αντίστοιχη κινητική ενέργεια, τη στιγμή t₁, η οποία συνδέεται με την μεταφορική κίνηση του δίσκου.

iii) Το έργο της δύναμης F₂ και το αντίστοιχο έργο της ροπής της δύναμης.

iv) Η κινητική ενέργεια του δίσκου τη στιγμή t₁.

Δίνεται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα ο οποίος περνά από το κέντρο του Ο, Ι= ½ mR².

Απάντηση:

ή

 Τα έργα των δυνάμεων και η κινητική ενέργεια

 Τα έργα των δυνάμεων και η κινητική ενέργεια

Ένα ζεύγος περιστρέφει έναν δίσκο

 

Σε λείο οριζόντιο επίπεδο ηρεμεί ελεύθερος ένας ομογενής δίσκος μάζας Μ=20kg και ακτίνας R=2m. Σε μια στιγμή t=0, ασκούμε στα άκρα Α και Β μιας διαμέτρου του, δύο σταθερές αντίθετες δυνάμεις με μέτρα F₁=F₂=14Ν, όπως στο σχήμα (σε κάτοψη).

i)  Να υπολογιστεί η αρχική επιτάχυνση του κέντρου Ο και η αντίστοιχη γωνιακή επιτάχυνση του δίσκου.

Μετά από λίγο τη στιγμή t₁ ο δίσκος έχει στραφεί κατά γωνία φ (ημφ=0,8 και συνθ=0,6), έχοντας γωνιακή ταχύτητα ω₁=1,5rad/s.  Για τη στιγμή αυτή:

ii)  Να βρεθεί η στροφορμή και ο ρυθμός μεταβολής της στροφορμής του δίσκου, ως προς κατακόρυφο άξονα ο οποίος περνά από το κέντρο του Ο.

iii) Να υπολογιστεί η κινητική ενέργεια του δίσκου και ο ρυθμός μεταβολής της κινητικής του ενέργειας.

iv) Μπορείτε να υπολογίστε την στιγμιαία ισχύ της δύναμης F₁ στη στιγμή t₁, χωρίς αναφορά σε ροπή δύναμης ή ροπή ζεύγους δυνάμεων;

Δίνεται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι= ½ ΜR².

Απάντηση:

ή

Ένα ζεύγος περιστρέφει έναν δίσκο

Ένα ζεύγος περιστρέφει έναν δίσκο

Οι ενέργειες σε μια εξαναγκασμένη ταλάντωση

 

Το σώμα Σ δεμένο στο άκρο κατακόρυφου ελατηρίου σταθεράς k, μπορεί να εκτελεί, απουσία αποσβέσεων, ΑΑΤ με συχνότητα 0,5Ηz. Στη διάταξη του διπλανού σχήματος, παρουσία αποσβέσεων, το σώμα μπορεί να εκτελεί εξαναγκασμένη ταλάντωση ορισμένου πλάτους Α₁, όταν ο τροχός Τ στρέφεται με περίοδο Τ₁=1s. Αν αυξήσουμε την περίοδο περιστροφής του τροχού στην τιμή Τ₂=1,25s, τότε:

i) Το πλάτος ταλάντωσης:

α) θα μειωθεί,   β) θα μείνει το ίδιο,   γ) θα αυξηθεί.

ii) Αν το πλάτος ταλάντωσης είναι Α₂ , τότε:

Α) Η μέγιστη ταχύτητα του σώματος θα είναι:

α) 2πf₂∙Α₂         β) 2πf₀∙Α₂       γ) άλλη τιμή.

Β) Για τις μέγιστες τιμές Δυναμικής και Κινητικής ενέργειας  θα ισχύει:

α)   Κ_max> U_max,       β)  Κ_max = U_max,     γ) Κ_max < U_max.

Να δικαιολογήσετε τις απαντήσει σας.

Απάντηση:

ή

Οι ενέργειες σε μια εξαναγκασμένη ταλάντωση

Οι ενέργειες σε μια εξαναγκασμένη ταλάντωση

Όταν μαζεύεται το νήμα

 

Σε λείο οριζόντιο επίπεδο ηρεμεί ένας ομογενής δίσκος, μάζας m=2kg και ακτίνας R=1m, ο οποίος μπορεί να στρέφεται γύρω από κατακόρυφο σωλήνα- άξονα z, χωρίς τριβές. Στο σωλήνα έχει δεθεί το ένα άκρο αβαρούς νήματος, μήκους ℓ=0,5m, στο άλλο άκρο του οποίου έχει δεθεί σώμα Σ ίσης μάζας m, το οποίο θεωρούμε υλικό σημείο αμελητέων διαστάσεων. Με τεντωμένο το νήμα, κτυπάμε το σώμα προσδίδοντάς του αρχική ταχύτητα μέτρου υ₀=2,8m/s, κάθετη στο νήμα, όπως στο σχήμα. Μεταξύ σώματος Σ και δίσκου αναπτύσσεται τριβή, ενώ κατά την περιστροφή του σώματος, το νήμα τυλίγεται στο σωλήνα. Μόλις σταματήσει η ολίσθηση του Σ πάνω στο δίσκο, το σύστημα έχει γωνιακή ταχύτητα μέτρου ω=2rad/s. Ζητούνται:

i)  Η αρχική στροφορμή του σώματος Σ, ως προς τον άξονα z καθώς και η τελική ολική στροφορμή του συστήματος, ως προς τον ίδιο άξονα.

ii) Το μήκος του νήματος που τυλίχθηκε γύρω από τον σωλήνα.

iii) Η απώλεια της μηχανικής ενέργειας λόγω τριβής.

iv) Κάποια στιγμή t₁ η στροφορμή του Σ, ως προς τον άξονα z, μειώνεται με ρυθμό 0,8kgm²/s². Να υπολογιστεί ο ρυθμός μεταβολής της στροφορμής του δίσκου, ως προς τον άξονα z, την ίδια στιγμή.

Δίνεται η ροπή αδράνειας του δίσκου ως προς κάθετο άξονα που περνά από το κέντρο του Ι= ½ mR², ενώ η ροπή της τάσης του νήματος, ως προς τον άξονα περιστροφής θεωρείται αμελητέα.

Απάντηση:

ή

 Όταν μαζεύεται το νήμα

 Όταν μαζεύεται το νήμα

Στα χνάρια του Νεκτάριου

Κατασκευάζουμε ένα τροχό ενώνοντας τις βάσεις δύο ομογενών κυλίνδρων, έτσι ώστε να αποκτήσουν κοινό άξονα όπως δείχνει το σχήμα. Ο μεγάλος κύλινδρος έχει ακτίνα R = 0,4 m και ο μικρός r = 0,2 m. Ο τροχός μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα, που ταυτίζεται με τον κοινό γεωμετρικό άξονα των κυλίνδρων. Η ροπή αδράνειας του συστήματος των ενωμένων κυλίνδρων ως προς τον άξονα αυτό είναι Ι = 0,6 kg∙m². Γύρω από τον μικρότερο κύλινδρο, είναι τυλιγμένο ένα αβαρές σχοινί, στο κάτω άκρο του οποίου είναι δεμένο ένα σφαιρίδιο Σ μάζας m₁ = 7,5 kg. Μια ομογενής δοκός ΑΒ που το βάρος της έχει μέτρο w = 150 Ν, στηρίζεται με άρθρωση σε κατακόρυφο τοίχο, και εφάπτεται στον μεγάλο κύλινδρο σε απόσταση d = 3ℓ/4 από τη άρθρωση. Το νήμα, δεν γλιστρά κατά την περιστροφή του συστήματος. Αρχικά συγκρατούμε τον τροχό ακίνητο, και τη χρονική στιγμή t = 0 τον αφήνουμε ελεύθερο, οπότε αρχίζει το νήμα να ξετυλίγεται. Να υπολογίσετε:

α. το μέτρο της δύναμης που ασκεί η ράβδος στο στερεό.

β. την δύναμη που δέχεται η ράβδος από την άρθρωση

γ. τη γωνιακή επιτάχυνση του συστήματος των δύο τροχών.

δ. Την ταχύτητα του σώματος Σ όταν έχει κατέβει κατά h = 0,16 m.

ε. Τον ρυθμό που παράγεται θερμότητα στο σημείο επαφής τροχού – δοκού, τη χρονική στιγμή που η ταχύτητα του σώματος Σ έχει μέτρο υ = 2 m/s.

Δίνεται ο συντελεστής τριβής ολίσθησης μεταξύ του τροχού και της δοκού είναι μ = 0,15 και g = 10 m/s².

Η συνέχεια εδώ.

Ο ρόλος του άξονα περιστροφής

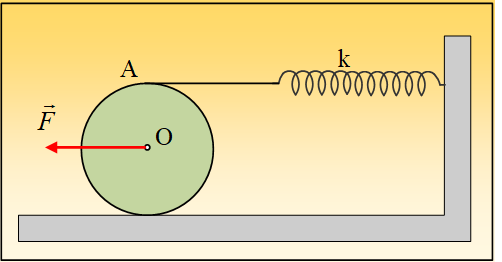
Σε επαφή με λείο οριζόντιο επίπεδο στρέφεται ένας ομογενής δίσκος, μάζας m με σταθερή γωνιακή ταχύτητα ω, γύρω από σταθερό (υπαρκτό) κατακόρυφο άξονα, χωρίς τριβές. Η στροφορμή του δίσκου στο (α) σχήμα γύρω από τον άξονα z, ο οποίος περνά από το κέντρο του, έχει μέτρο L_ο.

 

i)  Αν στο (β) σχήμα ο δίσκος στρέφεται γύρω από τον άξονα z₁ ο οποίος περνά από το σημείου Α, όπου (ΟΑ) = ½ R, με την ίδια γωνιακή ταχύτητα, τότε:

α) Για το μέτρο της στροφορμής του δίσκου L_β, γύρω από τον άξονα z₁ ισχύει:

a) L_β=L_o,    b) L_β=1,5L_o,      c) L_β=2L_o   d) L_β=2,5L_o.

β) Για την δύναμη που κάθε άξονας ασκεί στο δίσκο, ισχύει:

a) F_α=F_β=0,     b) F_α=F_β ≠0,     c) F_α= 0  και F_β ≠0,   d) F_α  ≠ 0  και F_β =0.

ii) Στα σχήματα (γ) και (δ), στο άκρο μιας ακτίνας του δίσκου, έχει προσκολληθεί ένα σώμα Σ, το οποίο θεωρούμε υλικό σημείο αμελητέων διαστάσεων, μάζας επίσης m, με αποτέλεσμα να παίρνουμε ένα στερεό s με κέντρο μάζας το σημείο Α. Το στερεό s στρέφεται επίσης με γωνιακή ταχύτητα ω, γύρω από τους αντίστοιχους άξονες z και z₁.

α) Για το μέτρο της στροφορμής του στερεού L_δ, γύρω από τον άξονα z₁ ισχύει:

a) L_δ=L_o,    b) L_δ=2L_o,      c) L_δ=3L_o   d) L_δ=4L_o.

β) Αν F_β το μέτρο της δύναμης που ασκεί ο άξονας z₁ στο δίσκο του (β) σχήματος, τότε για τα μέτρα των αντίστοιχων δυνάμεων στα σχήματα (γ) και (δ) ισχύουν:

a) F_γ=0 και F_δ=2F_β,     b) F_γ=2F_β,  F_δ=0,     c) F_γ= 0  και F_B =0,   d) F_γ  =4F_β  και F_δ =2F_β.

Απάντηση:

ή

 Ο ρόλος του άξονα περιστροφής

 Ο ρόλος του άξονα περιστροφής

Μια ισορροπία και μια επιτάχυνση μέσω ελατηρίου

Ο ομογενής κύλινδρος του σχήματος μάζας m=4kg και ακτίνας R, ισορροπεί σε οριζόντιο επίπεδο, ενώ γύρω του έχουμε τυλίξει ένα αβαρές νήμα στο άκρο του οποίου συνδέεται οριζόντιο ιδανικό ελατήριο, σταθεράς k=100Ν/m, με την επίδραση οριζόντιας δύναμης F=30Ν, η οποία ασκείται στο κέντρο μάζας του Ο.

i)   Να δικαιολογήσετε γιατί ο κύλινδρος εμφανίζει τριβή με το επίπεδο.

ii)  Να βρείτε την επιμήκυνση του ελατηρίου, καθώς και τον ελάχιστο συντελεστή οριακής στατικής τριβής μεταξύ κυλίνδρου και επιπέδου, για την παραπάνω ισορροπία.

iii) Κάποια στιγμή σταματάμε την εξάσκηση της δύναμης F. Να υπολογιστεί η επιτάχυνση την οποία θα αποκτήσει το ανώτερο σημείο του κυλίνδρου Α, καθώς και η τριβή η οποία θα ασκηθεί στον κύλινδρο, αμέσως μόλις αφεθεί να κινηθεί.

Δίνεται η ροπή αδράνειας του κυλίνδρου Ι_cm= ½ mR² και g=10m/s².

Απάντηση:

ή

 Μια ισορροπία και μια επιτάχυνση μέσω ελατηρίου

 Μια ισορροπία και μια επιτάχυνση μέσω ελατηρίου

Δύο κινήσεις του ίδιου κυλίνδρου

 

 Ο κύλινδρος του σχήματος  έχει μάζα m=4kg και ακτίνα R και στο κεντρικό του τμήμα φέρει εγκοπή ακτίνας r=0,5R. Στην εγκοπή έχουμε τυλίξει ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου ασκούμε μια οριζόντια σταθερή δύναμη μέτρου F=16Ν. Στο σχήμα βλέπετε τρία σημεία Α, Β και Γ, όπου το Α είναι ένα σημείο επαφής του κυλίνδρου με το επίπεδο, το Β το σημείο όπου το νήμα έρχεται σε επαφή με το κύλινδρο και το Γ είναι αντιδιαμετρικό του σημείου Α.

i)  Αν το επίπεδο είναι λείο:

α) Να βρεθούν οι αρχικές επιταχύνσεις των σημείων Α και Β.

β) Να υπολογιστούν οι ταχύτητες των αντίστοιχων σημείων στις θέσεις των Α, Β και Γ τη χρονική στιγμή t₁=5s.

ii) Ποιες οι αντίστοιχες απαντήσεις αν ο κύλινδρος παρουσίαζε με το επίπεδο συντελεστή τριβής μ=0,2;

Δίνεται η ροπή αδράνειας του κυλίνδρου γύρω από τον άξονα περιστροφής του Ι= ½ mR² και g=10m/s².

Απάντηση:

ή

 Δύο κινήσεις του ίδιου κυλίνδρου

 Δύο κινήσεις του ίδιου κυλίνδρου

Όταν εμφανιστεί η τριβή…

 

Γύρω από ένα κύλινδρο, ο οποίος ηρεμεί σε λείο οριζόντιο επίπεδο Α, έχουμε τυλίξει ένα αβαρές νήμα. Σε μια στιγμή τραβάμε το νήμα ασκώντας στον κύλινδρο μια σταθερή οριζόντια δύναμη F, όπως στο σχήμα.

i)  Η κίνηση του κυλίνδρου θα είναι μια κύλιση (χωρίς ολίσθηση) ή όχι και γιατί;

ii) Μετά από λίγο ο κύλινδρος περνά σε δεύτερο μη λείο οριζόντιο επίπεδο Β, όπως στο σχήμα, οπότε:

α) Θα δεχτεί στατική τριβή με φορά προς τα αριστερά.

β) Θα δεχτεί στατική τριβή με φορά προς τα δεξιά.

γ) Θα δεχτεί τριβή ολίσθησης με φορά προς τα αριστερά.

δ) Θα δεχτεί τριβή ολίσθησης με φορά προς τα δεξιά.

Να δικαιολογήσετε την επιλογή σας.

Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς άξονα που ενώνει τα κέντρα των δύο βάσεών του Ι= ½ ΜR².

 Απάντηση:

ή

 Όταν εμφανιστεί η τριβή…

 Όταν εμφανιστεί η τριβή…

Η δύναμη από το σκαλοπάτι και η τριβή.

 

Γύρω από ένα κύλινδρο έχουμε τυλίξει ένα νήμα, στο άκρο του οποίου ασκούμε μια οριζόντια δύναμη F. Ο κύλινδρος ισορροπεί σε λείο οριζόντιο επίπεδο, σε επαφή με εμπόδιο ύψους h, όπως στο σχήμα.

i)  Η δύναμη που δέχεται ο κύλινδρος από το εμπόδιο είναι:

α)  η δύναμη F₁ με κατεύθυνση προς το κέντρο Ο του κυλίνδρου.

β) η δύναμη F₂ με κατεύθυνση προς το ανώτερο σημείο Β του κυλίνδρου.

γ) Καμιά από τις δύο παραπάνω περιπτώσεις.

ii) Να αποδείξετε ότι μεταξύ κυλίνδρου και σκαλοπατιού αναπτύσσεται δύναμη τριβής.

iii) Για το μέτρο της ασκούμενης τριβής ισχύει:

α) Τ < F,   β) Τ = F,  γ) Τ > F.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Η δύναμη από το σκαλοπάτι και η τριβή.

 Η δύναμη από το σκαλοπάτι και  η τριβή.

Μερικές ερωτήσεις στη δυναμική στερεού.

 

Στις παρακάτω ερωτήσεις ένας ομογενής δίσκος μπορεί να κινείται σε οριζόντιο μη λείο επίπεδο.

Ερώτηση 1^η:

Ο δίσκος αρχικά ηρεμεί και κάποια στιγμή δέχεται στο κέντρο του οριζόντια δύναμη F, με αποτέλεσμα να αρχίσει να κυλίεται.

i) Η συνισταμένη δύναμη που ασκείται στον δίσκο είναι ή όχι οριζόντια;

ii) Ο φορέας της συνισταμένης δύναμης στον δίσκο, περνά από το σημείο:

α) το κέντρο Ο του δίσκου,    β) Α,      γ) το Β.

όπου τα σημεία Α και Β είναι σημεία μιας κατακόρυφης διαμέτρου, όπως στο σχήμα.

Απάντηση:

ή

 Μερικές ερωτήσεις στη δυναμική στερεού.

 Μερικές ερωτήσεις στη δυναμική στερεού.

Η ροπή αδράνειας ενός τριγώνου

 

Στο σχήμα βλέπετε ένα ορθογώνιο τρίγωνο, οι πλευρές του οποίου έχουν προκύψει από την ίδια ομογενή λεπτή ράβδο, έχοντας μήκη (ΑΒ)= 3m, (ΑΓ)= 4m και (ΒΓ)= 5m. Το τρίγωνο έχει μάζα 24kg και μπορεί να στρέφεται γύρω από οριζόντιο άξονα ο οποίος περνά από την κορυφή Α, όπως στο πρώτο σχήμα, ενώ συγκρατείται σε τέτοια θέση, ώστε η πλευρά ΑΒ να είναι οριζόντια.

i)  Να υπολογιστεί η μάζα κάθε ράβδου-πλευράς του τριγώνου.

ii)  Αν η  ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα ο οποίος περνά από το μέσον της, δίνεται από την σχέση Ι_cm= (mℓ²/12), να υπολογιστεί η αρχική επιτάχυνση της κορυφής Β, μόλις το τρίγωνο αφεθεί να περιστραφεί.

Στο δεύτερο σχήμα, το τρίγωνο μπορεί να στρέφεται γύρω από κατακόρυφο άξονα z, ο οποίος ταυτίζεται με την πλευρά ΑΓ.

iii) Ξεκινώντας από τον ορισμό της ροπής αδράνειας, μπορείτε να υπολογίσετε τη ροπή αδράνειας της ράβδου ΒΓ ως προς τον άξονα z, συσχετίζοντάς την με την αντίστοιχη ροπή αδράνειάς της ως προς κάθετο άξονα ο οποίος περνά από το άκρο της Γ;

iv) Πόση δύναμη, κάθετη στο επίπεδο του τριγώνου και με σταθερό μέτρο, πρέπει να ασκηθεί στην κορυφή Β, ώστε το τρίγωνο να περιστραφεί κατά 120° σε χρόνο Δt=2s;

Δίνεται g=10m/s².

Απάντηση:

ή

 Η  ροπή αδράνειας ενός τριγώνου

 Η  ροπή αδράνειας ενός τριγώνου

Γύρω από ποιο άξονα περιστρέφεται η ράβδος;

 

Σε λείο οριζόντιο επίπεδο, ηρεμεί μια ομογενής ράβδος μήκους ℓ=2m και μάζας m=3kg ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή δέχεται μια οριζόντια δύναμη μέτρου F=6Ν, κάθετη στην ράβδο, στο άκρο της Α, όπως στο σχήμα. Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα που περνά από  το μέσον της Ο,  Ι_cm= mℓ²/12.

i)  Να υπολογιστεί η επιτάχυνση του κέντρου μάζας Ο της ράβδου, καθώς και η επιτάχυνση του άκρου Α, αμέσως μόλις ασκηθεί η δύναμη F.

ii) Υποστηρίζεται ότι η κίνηση της ράβδου μπορεί να θεωρηθεί μόνο στροφική. Να εξετάσετε αν αυτό είναι σωστό ή όχι.

iii) Μπορείτε να υπολογίσετε την γωνιακή επιτάχυνση της ράβδου, θεωρώντας ως σημείο αναφοράς το άκρο Α της ράβδου και όχι το κέντρο μάζας Ο;

iv) Αν σας δίνετε ότι το άκρο Α της ράβδου αποκτά επιτάχυνση α_Α=4m/s², όταν αλλάξουμε το μέτρο της ασκούμενης δύναμης, να βρείτε την αρχική επιτάχυνση του κέντρου Ο της ράβδου, θεωρώντας την κίνηση σύνθετη, μια μεταφορική και μια περιστροφή γύρω από κατακόρυφο άξονα ο οποίος περνά από το σημείο Α.

Τα δύο τελευταία ερωτήματα απευθύνονται μόνο σε καθηγητές.

Απάντηση:

ή

 Γύρω από ποιο άξονα περιστρέφεται η ράβδος;

 Γύρω από ποιο άξονα περιστρέφεται η ράβδος;

Ανοίγοντας ένα παράθυρο στην πόρτα

 

Μια ξύλινη ομογενής πόρτα μάζας M=30kg με άνοιγμα α=1m και ύψος h=2m, στηρίζεται σε δύο μεντεσέδες Α και Β, οι οποίοι απέχουν από το πάνω και το κάτω μέρος της, αποστάσεις d=0,25m, όπως στο σχήμα.

i)   Αν ο κάτω μεντεσές Β ασκεί στην πόρτα οριζόντια  δύναμη, να βρεθεί η δύναμη που δέχεται η πόρτα από τον πάνω μεντεσέ Α.

ii) Το πόσο εύκολα ανοιγοκλείνει η πόρτα καθορίζεται από την ροπή αδράνειας που εμφανίζει ως προς τον κατακόρυφο άξονα περιστροφής της, ο οποίος περνά από τους μεντεσέδες. Να αποδείξετε ότι η παραπάνω ροπή αδράνειας, είναι ανεξάρτητη του ύψους της πόρτας.

iii) Θέλοντας να κάνουμε ελαφρύτερη την πόρτα, αλλά και για να αερίζεται το δωμάτιο, ανοίγουμε ένα τετράγωνο παράθυρο, κόβοντας το ξύλο, με πλευρά β=0,5m, όπως στο δεύτερο σχήμα (το παράθυρο ισαπέχει από τις δύο κατακόρυφες πλευρές της πόρτας). 

α) Πόσο τοις  % μειώθηκε το βάρος της;

β) Πόσο της % μειώθηκε η ροπή αδράνειάς της, ως προς τον άξονα περιστροφής της;

Δίνεται g=10m/s², ενώ η ροπή αδράνειας μιας λεπτής ομογενούς σανίδας ως προς κάθετο άξονα ο οποίος περνά από το μέσον της Ι_cm=ml²/12.

Απάντηση:

ή

 Ανοίγοντας ένα παράθυρο στην πόρτα

 Ανοίγοντας ένα παράθυρο στην πόρτα

Ένα τρίγωνο και η ροπή αδράνειάς του

 

Σε λείο οριζόντιο επίπεδο ηρεμεί ένα στερεό s, το οποίο έχει σχήμα ισοπλεύρου τριγώνου, αποτελούμενο από τρεις ίδιες ομογενείς λεπτές ράβδους, μήκους ℓ=1m και μάζας m=2kg η καθεμιά. Το στερεό μπορεί να στρέφεται γύρω από σταθερό κατακόρυφο άξονα z, ο οποίος περνά από την κορυφή Α του τριγώνου. Σε μια στιγμή t₀=0 ασκούμε στην κορυφή Β δύναμη σταθερού μέτρου F=1,5π (Ν), η οποία είναι διαρκώς κάθετη στην πλευρά ΑΒ, όπως στο σχήμα. Το στερεό εκτελεί 4,5 περιστροφές μέχρι τη χρονική στιγμή t₁=6s.

i) Να βρεθεί η γωνιακή επιτάχυνση του τριγώνου, καθώς και η επιτάχυνση της κορυφής Β που έχει την κατεύθυνση της ασκούμενης δύναμης F.

ii) Να υπολογισθεί η επιτάχυνση της κορυφής Β που είναι κάθετη στην δύναμη F, τη χρονική στιγμή t₁.

iii) Πόση είναι η ροπή αδράνειας του στερεού ως προς τον άξονα περιστροφής z;

iv) Αν η ροπή αδράνειας της ράβδου ΑΒ ως προς τον άξονα z δίνεται από την σχέση Ι_ΑΒ=λ∙mℓ², να βρεθεί η σταθερά αναλογίας λ.

Απάντηση:

ή

 Ένα τρίγωνο και η ροπή αδράνειάς του
 Ένα τρίγωνο και η ροπή αδράνειάς του

Τα θεωρήματα παραλλήλων και καθέτων αξόνων

 

Ας ξεκινήσουμε από το «εντός ύλης» θεώρημα των παραλλήλων αξόνων (θεώρημα Steiner).

Έστω ένα επίπεδο στερεό, τυχαίου σχήματος και Κ το κέντρο μάζας του. Έστω επίσης ένα σύστημα ορθογωνίων αξόνων x,y,z, με αρχή το σημείο Ο, όπου μας ενδιαφέρει η ροπή αδράνειας του στερεού ως προς τον άξονα y. Χωρίζουμε το στερεό σε στοιχειώδεις μάζες m_i και έστω μια από αυτές στο σχήμα με διάνυσμα θέσης r όπου, με βάση το σχήμα ισχύει:

Διαβάστε τη συνέχεια…

ή

  Τα θεωρήματα παραλλήλων και καθέτων αξόνων

  Τα θεωρήματα παραλλήλων και καθέτων αξόνων