Η μέγιστη ενέργεια ταλάντωσης

 

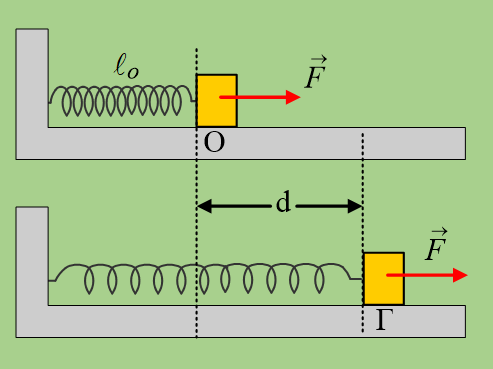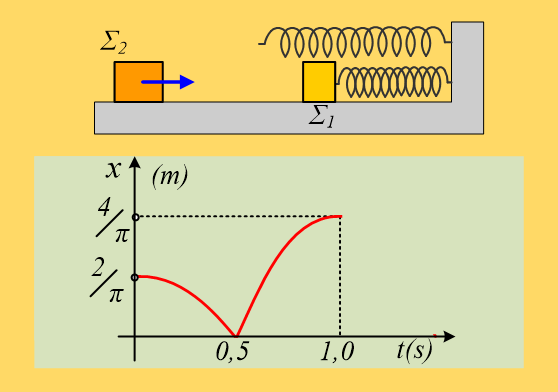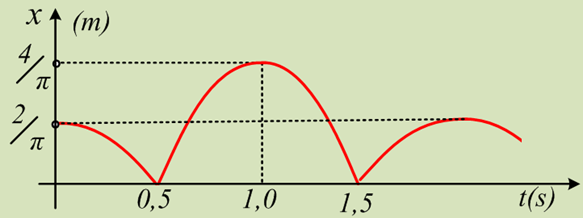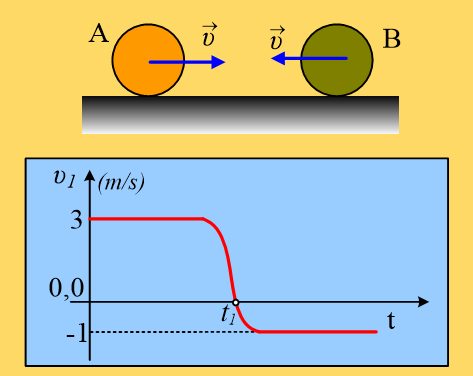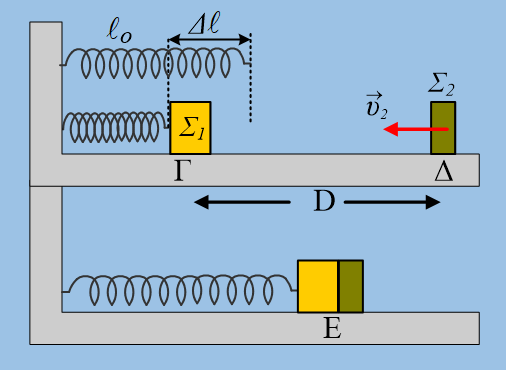
Ένα σώμα Σ₁ μάζας m₁=2kg είναι δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=200Ν/m και ηρεμεί σε λείο οριζόντιο επίπεδο. Ένα δεύτερο σώμα Σ₂ μάζας m₂=0,5kg κινείται με ταχύτητα μέτρου υ₂=8m/s κατά μήκος του άξονα του ελατηρίου, πλησιάζοντας το σώμα Σ₁. Μετακινούμε το Σ₁ συμπιέζοντας το ελατήριο κατά Δℓ=0,5m, φέρνοντάς το στη θέση Γ. Σε μια στιγμή t₀=0, όπου τα δυο σώματα απέχουν κατά (ΓΔ)=D,  αφήνουμε ελεύθερο το Σ₁ να εκτελέσει ΑΑΤ, με αποτέλεσμα τα σώματα να συγκρούονται κεντρικά και ελαστικά τη χρονική στιγμή t₁=0,314s.

i)  Να υπολογιστεί η απόσταση D.

ii) Να υπολογιστεί η ενέργεια ταλάντωσης του Σ₁ αμέσως μετά την κρούση, καθώς και η ταχύτητα με την οποία φτάνει στην αρχική του θέση Γ.

ii) Επαναλαμβάνουμε τη διαδικασία, αλλά τώρα αφήνουμε το Σ₁ να κινηθεί όταν έχουμε διαφορετική απόσταση μεταξύ των σωμάτων, με αποτέλεσμα το Σ₁ να αποκτήσει τη μέγιστη δυνατή ενέργεια ταλάντωσης, μετά την κρούση.

α) Να βρεθεί η μέγιστη αυτή ενέργεια ταλάντωσης του Σ₁.

β) Να βρεθεί η θέση της κρούσης, καθώς και η ταχύτητα του Σ₁ ελάχιστα πριν την κρούση.

Απάντηση:

ή

Η μέγιστη ενέργεια ταλάντωσης

Η μέγιστη ενέργεια  ταλάντωσης

Δυο διαδοχικές ταλαντώσεις

 

Ένα σώμα μάζας 2kg ηρεμεί σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=20Ν/m, στη θέση Ο. Ασκούμε στο σώμα για t₀=0, μια σταθερή οριζόντια δύναμη μέτρου F=8Ν με αποτέλεσμα να επιμηκύνεται το ελατήριο, μέχρι τη στιγμή t₁ που το σώμα έχοντας μετακινηθεί κατά d=0,8m, φτάνει στη θέση Γ, όπου παύει να ασκείται πάνω του η δύναμη F.

i) Να υπολογιστεί η επιτάχυνση του σώματος:

α) στην αρχική θέση, μόλις ασκηθεί η δύναμη F, 

β) όταν το ελατήριο έχει επιμήκυνση Δl₁=0,4m, 

γ) στην θέση Γ, πριν καταργηθεί η δύναμη F και αμέσως μετά την κατάργησή της.

ii) Να βρεθεί η μέγιστη κινητική ενέργεια του σώματος για το διάστημα που ασκείται πάνω του η δύναμη F.

iii) Πόσο χρόνο ασκήθηκε στο σώμα η δύναμη F;

iv) Να γίνει η γραφική παράσταση x=x(t) της απομάκρυνσης του σώματος από την αρχική θέση ισορροπίας του Ο, σε συνάρτηση με το χρόνο, μέχρι τη χρονική στιγμή t₂= 2s.

Θεωρείστε ότι π²≈10.

Απάντηση:

ή

Δυο διαδοχικές ταλαντώσεις

Δυο διαδοχικές ταλαντώσεις

Το διάγραμμα απομάκρυνσης και δυο κρούσεις.

 

Ένα σώμα Σ₁ είναι δεμένο στο άκρο ενός ιδανικού ελατηρίου σταθεράς k=2∙π²≈20Ν/m και συγκρατείται σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει το ελατήριο κατά (2/π)m. Ένα δεύτερο σώμα Σ₂ κινείται στο ίδιο οριζόντιο επίπεδο, κατά μήκος του άξονα του ελατηρίου πλησιάζοντας το σώμα Σ₁. Σε μια στιγμή t₀=0, αφήνουμε το Σ₁ να ταλαντωθεί και στο διπλανό σχήμα βλέπετε τη γραφική παράσταση της απομάκρυνσής του από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο, μέχρι τη στιγμή t₂=1s, όπου μηδενίζεται στιγμιαία η ταχύτητά του για πρώτη φορά, μετά την κρούση του με το σώμα Σ₂.

i)  Να βρεθεί η μάζα του σώματος Σ₁, καθώς και η ταχύτητά του ελάχιστα πριν και αμέσως μετά την κρούση του με το σώμα Σ₂.

ii) Υποστηρίζεται ότι η κρούση μεταξύ των δύο σωμάτων μπορεί να είναι πλαστική. Να εξετάσετε αν αυτό μπορεί να ισχύει.

iii) Παρακολουθώντας την παραπέρα κίνηση του σώματος Σ₁, διαπιστώνουμε ότι η απομάκρυνση, από τη θέση ισορροπίας του, μεταβάλλεται συνολικά όπως στο διπλανό σχήμα. Αν οι κρούσεις μεταξύ των σωμάτων είναι ελαστικές:

 

α) Ποια η κινητική ενέργεια του σώματος Σ₂ πριν την πρώτη του κρούση με το Σ₁ και ποια αμέσως μετά την κρούση;

β) Να υπολογιστεί η μάζα του σώματος Σ₂ και η τελική του ταχύτητα.

Απάντηση:

ή

 Το  διάγραμμα απομάκρυνσης και δυο κρούσεις.

 Το  διάγραμμα απομάκρυνσης και δυο κρούσεις.

Μια κρούση και πληροφορίες από ένα διάγραμμα

 

Σε λείο οριζόντιο επίπεδο κινούνται δυο ελαστικές σφαίρες με ίσες ακτίνες, η μία προς την άλλη, με ταχύτητες ίσου μέτρου, όπως στο σχήμα. Σε μια στιγμή συγκρούονται κεντρικά και ελαστικά και στο διάγραμμα φαίνεται η ταχύτητα της Α σφαίρας, η οποία έχει μάζα m₁=2kg, σε συνάρτηση με το χρόνο.

i)  Τι ποσοστό της αρχικής κινητικής ενέργειας της Α σφαίρας μεταφέρεται στην Β σφαίρα, στη διάρκεια της κρούσης;

ii)  Αφού υπολογίσετε την μάζα της Β σφαίρας, να χαράξετε ένα ποιοτικό διάγραμμα για την ταχύτητα της Β σφαίρας σε συνάρτηση με το χρόνο.

iii) Να υπολογιστεί η ταχύτητα της Β σφαίρας τη στιγμή t₁ που μηδενίζεται η ταχύτητα της σφαίρας Α.

iv) Πόση είναι η δυναμική ενέργεια ελαστικής παραμόρφωσης των σφαιρών τη στιγμή t₁;

v) Ένας μαθητής κοιτάζοντας το διάγραμμα που δίνεται, συμπεραίνει ότι τη στιγμή t₁ η γραφική παράσταση τέμνει σχεδόν κάθετα τον άξονα του χρόνου. Συμφωνείτε ή όχι με την εκτίμηση αυτή; Να δικαιολογήσετε την άποψή σας.

Απάντηση:

ή

 Μια κρούση και πληροφορίες από ένα διάγραμμα

 Μια κρούση και πληροφορίες από ένα διάγραμμα

Στον παλμό του Πάλμου...

Η ράβδος ΚΛ μήκους ℓ=1m, μάζας m=2kg και αμελητέας ωμικής αντίστασης μπορεί να κινείται χωρίς τριβές, σε επαφή με τους λείους κατακόρυφους αγωγούς Αx και Γy παραμένοντας συνεχώς κάθετη σε αυτούς. Τα άκρα Α και Γ των αγωγών

Ισορροπίες με τριβές και κρούση.

Πάνω σε ένα μη λείο οριζόντιο επίπεδο, ηρεμεί ένα σώμα Σ₁ μάζας m₁=2kg, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=20Ν/m, το οποίο έχει επιμηκύνει κατά x₁=0,2m. Ένα δεύτερο σώμα Σ₂ μάζας m₂=1kg κινείται κατά μήκος του άξονα του ελατηρίου με κατεύθυνση προς το σώμα Σ₁, με το οποίο μετά από λίγο συγκρούεται μετωπικά και ελαστικά. Τα δυο σώματα παρουσιάζουν τον ίδιο συντελεστή τριβής ολίσθησης με το επίπεδο μ=0,65. Μετά την κρούση το Σ₁ διανύει απόσταση (ΑΒ)= s=0,6m, μέχρι να μηδενιστεί η ταχύτητά του, στη θέση Β.

i)  Να υπολογιστεί η τριβή που ασκείται στο σώμα Σ₁, στη θέση Α, πριν την κρούση.

ii)  Να βρεθεί η ταχύτητα την οποία αποκτά το σώμα Σ₁, αμέσως μετά την κρούση, καθώς και η αντίστοιχη επιτάχυνσή του.

iii) Τι ποσοστό της κινητικής ενέργειας του Σ₂ ελάχιστα πριν την κρούση, μεταφέρεται στο σώμα Σ₁;

iv) Να βρεθεί η τελική απόσταση μεταξύ των δύο σωμάτων, μετά την ακινητοποίησή τους.

Δίνεται g=10m/s².

Απάντηση:

ή

Ισορροπίες με τριβές και κρούση.

Ισορροπίες με τριβές και κρούση.

Ελάχιστο ποσοστό απώλειας…

Τρεις σφαίρες Σ₁, Σ₂ και Σ₃ κινούνται σε λείο οριζόντιο επίπεδο χωρίς να περιστρέφονται. Οι μάζες των σφαιρών Σ₁ και Σ₃­­­­ είναι m₁=2kg και m₃=3kg αντίστοιχα, ενώ τα μέτρα των ταχυτήτων τους είναι υ₁=5m/s και υ₃=4m/s και κινούνται όπως φαίνεται στο σχήμα. Το σώμα Σ₂ έχει μάζα m₂­=5kg, μέτρο ταχύτητας υ₂=8m/s και η φορά κίνησής του είναι άγνωστη. Αν γνωρίζουμε ότι και τα τρία σώματα συνενώνονται και όλες οι πιθανές κρούσεις είναι πλαστικές τότε:

i) Το ποσό απώλειας ενέργειας του συστήματος είναι:

            α) Ε_απωλ.=120,8J                      β) Ε_απωλ.=136,8J                      γ) E_απωλ.=147,75J

Δικαιολογείστε την επιλογή σας.

ii) Να βρείτε που θα έπρεπε να είναι το Σ₂ και πως θα έπρεπε να κινείται, ώστε το ποσοστό απώλειας ενέργειας του συστήματος αν δημιουργείται συσσωμάτωμα να είναι ελάχιστο.

Απάντηση

Δύο κρούσεις, ένας έλεγχος

Στη θέση Ο, σε  ορισμένο ύψος από το έδαφος, συγκρατούμε δυο σφαίρες Α και Β με μάζες m₁=1kg και m₂=2kg. Σε μια στιγμή αφήνουμε την Β να πέσει και μετά από λίγο αφήνουμε την Α. Η σφαίρα Β συγκρούεται με το έδαφος και επιστρέφοντας συγκρούεται κεντρικά και ελαστικά με την Α, η οποία κατέρχεται, έχοντας τη στιγμή της κρούσης ταχύτητα μέτρου υ₁=3m/s. Μετά την κρούση η σφαίρα Α επιστρέφει στο σημείο Ο με μηδενική ταχύτητα.

i)   Να υπολογιστεί η κατακόρυφη απόσταση y μεταξύ της αρχικής θέσης Ο και της θέσης της κρούσης, των δύο σφαιρών.

ii) Να αποδείξετε ότι η κρούση μεταξύ της σφαίρας Β και του εδάφους, είναι ανελαστική.

iii) Να υπολογίσετε την μεταβολή της ορμής της Β σφαίρας κατά την κρούση των δύο σφαιρών.

iv) Να υπολογιστεί η απώλεια της μηχανικής ενέργειας κατά την κρούση της σφαίρας Β με το έδαφος.

Δίνεται g=10m/s².

Απάντηση:

ή

 Δύο κρούσεις, ένας έλεγχος

 Δύο κρούσεις, ένας έλεγχος

Η πτώση δύο πλαισίων

1) Ένας κατακόρυφος αγωγός, πολύ μεγάλου μήκους, διαρρέεται από συνεχές ρεύμα σταθερής έντασης Ι, με φορά προς τα πάνω. Δίπλα στον αγωγό, σε μικρή απόσταση, κρατάμε ένα χάλκινο πλαίσιο, έτσι ώστε ο αγωγός να βρίσκεται στο επίπεδο που ορίζει το πλαίσιο. Σε μια  στιγμή αφήνουμε το πλαίσιο να πέσει.

i)  Το πλαίσιο θα αρχίσει να διαρρέεται από ρεύμα λόγω επαγωγής.

ii)  Το πλαίσιο θα πλησιάσει τον αγωγό εξαιτίας της δύναμης Laplace που θα δεχτεί από το μαγνητικό πεδίο του αγωγού.

iii) Το πλαίσιο θα απομακρυνθεί από τον αγωγό εξαιτίας της δύναμης Laplace, που θα δεχτεί από το μαγνητικό πεδίο του αγωγού.

iv) Η κίνηση του πλαισίου θα είναι ελεύθερη πτώση.

Ποιες από τις παραπάνω προτάσεις είναι σωστές; Να δώσετε σύντομες δικαιολογήσεις.

Η αντίσταση του αέρα θεωρείται αμελητέα.

Συνέχεια:

ή

Η πτώση δύο πλαισίων

Η πτώση δύο πλαισίων

Η κίνηση του αγωγού και η μαγνητική ροή.

Ο αγωγός ΚΛ μήκους ℓ, μπορεί να κινείται οριζόντια, μέσα σε ένα ομογενές κατακόρυφο μαγνητικό πεδίο έντασης Β, σε επαφή με δυο παράλληλους αγωγούς Αx και Γy. Μεταξύ των άκρων Α και Γ συνδέεται αντιστάτης, ενώ στον ΚΛ, μπορούμε να ασκούμε μια οριζόντια δύναμη F (η δύναμη μπορεί να είναι και αντίθετης φοράς, από αυτήν που φαίνεται στο σχήμα). Παρακάτω δίνονται τρία διαγράμματα Φ=Φ(t) για τη μαγνητική ροή που περνά από το ορθογώνιο ΑΚΛΓ, με την προϋπόθεση ότι η κάθετη στην επιφάνεια έχει φορά ίδια με την ένταση του πεδίου.

1) Αναφερόμενοι στο (α) σχήμα:

α) Ο αγωγός ΚΛ κινείται προς τα δεξιά.

β) Η κίνηση του ΚΛ είναι ευθύγραμμη ομαλή.

γ) Στον αγωγό ΚΛ πρέπει να ασκούμε σταθερού μέτρου δύναμη F, με φορά προς τα δεξιά.

2) Αναφερόμενοι στην περίπτωση του (β) διαγράμματος:

α) Ο αγωγός ΚΛ κινείται προς τα αριστερά.

β) Από 0-t₁ ο αγωγός έχει σταθερή επιτάχυνση με φορά προς τα δεξιά.

γ) Στον αγωγό ΚΛ πρέπει να ασκούμε σταθερού μέτρου δύναμη F, με φορά προς τα αριστερά.

δ) Τη στιγμή t₂ ο αγωγός είναι ακίνητος σε κάποια απόσταση από τον αντιστάτη.

3) Για την (γ) περίπτωση της ροής, όπου η καμπύλη είναι αρμονική.

α) Τη στιγμή t=0 ο αγωγός ΚΛ έχει ταχύτητα προς τα δεξιά.

β) Τη στιγμή t₁ ο αγωγός έχει μηδενική ταχύτητα.

γ) τη στιγμή t₂ ο αγωγός έχει επιστρέψει στην αρχική του θέση.

δ) Το έργο της δύναμης F από 0-t₂ είναι ίσο με μηδέν.

Να χαρακτηρίστε τις παραπάνω προτάσεις ως σωστές ή λανθασμένες, δίνοντας και σύντομες δικαιολογήσεις.

Απάντηση:

ή

 Η κίνηση του αγωγού και η μαγνητική ροή.

 Η κίνηση του αγωγού και η μαγνητική ροή.

Ο ευθύγραμμος αγωγός και το πλαίσιο

Δίπλα  σε ένα ευθύγραμμο αγωγό πολύ μεγάλου μήκους που διαρρέεται από ηλεκτρικό ρεύμα, υπάρχει ένα ορθογώνιο αγώγιμο πλαίσιο ΑΓΔΕ. Ο αγωγός και το πλαίσιο ορίζουν κατακόρυφο επίπεδο. 

i) Να εξετάσετε αν το πλαίσιο διαρρέεται από ηλεκτρικό ρεύμα, όταν  ο ευθύγραμμος αγωγός:

α)   διαρρέεται από συνεχές ρεύμα έντασης Ι=2Α, με φορά προς τα πάνω.

β)  διαρρέεται από ρεύμα της μορφής i=2ημ100πt, όπου η θετική φορά είναι προς τα πάνω.

ii) Στην δεύτερη περίπτωση με το εναλλασσόμενο ρεύμα:

α)  Να βρεθεί η φορά του ρεύματος που διαρρέει το πλαίσιο τη χρονική στιγμή t₁= 1/75s.

β)  Να εξετασθεί αν η πλευρά ΑΕ του πλαισίου δέχεται δύναμη από το μαγνητικό πεδίο του ευθύγραμμου αγωγού, τη χρονική στιγμή t₂=0,025s και αν ναι, να προσδιοριστεί η κατεύθυνσή της.

Απάντηση:

ή

 Ο ευθύγραμμος αγωγός και το πλαίσιο
 Ο ευθύγραμμος αγωγός και το πλαίσιο

Μια ακόμη κατακόρυφη κίνηση ράβδου

Η ράβδος ΚΛ μήκους ℓ = 1m , μάζας m = 2 kg και ωμικής αντίστασης R = 2Ω μπορεί να κινείται χωρίς τριβές, σε επαφή με τους λείους κατακόρυφους αγωγούς Αx και Γy παραμένοντας συνεχώς κάθετη σε αυτούς. Τα άκρα Α και Γ των αγωγών συνδέονται μέσω ενός βαλλιστικού γαλβανομέτρου.  Το γαλβανόμετρο και οι αγωγοί Αx και  Γy δεν παρουσιάζουν ωμική αντίσταση ενώ το μόνο τμήμα του συστήματος που μπορεί να κινείται είναι η ράβδος.  Στο χώρο του συστήματος υπάρχει ομογενές μαγνητικό πεδίο έντασης B = 2Τ, με οριζόντιες δυναμικές γραμμές και φορά όπως στο σχήμα.  Τη χρονική στιγμή t₀ = 0 η ράβδος αφήνεται ελεύθερη να κινηθεί, ενώ τη χρονική στιγμή t_ορ η ταχύτητα της σταθεροποιείται. Μέχρι τη χρονική στιγμή t_ορ έχει περάσει από το γαλβανόμετρο φορτίο q =  40C.

α) Ποια η σταθερή ταχύτητα που αποκτά η ράβδος;

β) Ποια η απώλεια μηχανικής ενέργειας του συστήματος μέχρι τη χρονική στιγμή t_ορ ;

γ) Ποια η χρονική στιγμή t_ορ;

δ) Αν από την αρχή του φαινομένου μέχρι τη χρονική στιγμή t₁ = 1,6s έχει περάσει από το γαλβανόμετρο φορτίο q₁ = 8C να βρείτε:

i)  Τις απώλειες μηχανικής ενέργειας του συστήματος μέχρι τη χρονική στιγμή t₁.

ii)  Τους ρυθμούς μεταβολής της δυναμικής ενέργειας και της κινητικής ενέργειας της ράβδου καθώς και το ρυθμό απωλειών λόγω φαινομένου Joule στο σύστημα τη χρονική στιγμή t₁.

Δίνεται g =10 m/s². 

Απάντηση     word    pdf

Ανάλυση από τον Κώστα Ψυλάκο εδώ 

Ένα παλιό test στο εναλλασσόμενο

Στο διπλανό σχήμα, δίνονται ένα κύκλωμα Ε.Ρ. και η γραφική παράσταση της στιγμιαίας τάσης στα άκρα του αντιστάτη R με αντίσταση R=5Ω, σε συνάρτηση με το χρόνο.

i)  Ποιες προτάσεις είναι σωστές και ποιες λάθος:

α)   Η περίοδος της τάσης είναι 0,03s.

β)  Η συχνότητα της τάσης είναι 50Ηz.

γ)  Η μέγιστη τιμή της έντασης του ρεύματος που διαρρέει το κύκλωμα είναι ίση με 4 Α.

δ) Η ενεργός ένταση του ρεύματος είναι 4 Α.

ii)   Ποια είναι η ένδειξη του αμπερομέτρου;

iii)   Βρείτε την εξίσωση της έντασης του ρεύματος που διαρρέει το κύκλωμα σε συνάρτηση με το χρόνο.

iv)   Σε μια στιγμή t₁ η στιγμιαία ισχύς του ρεύματος είναι ίση με 20W για πρώτη φορά. Πόση είναι η στιγμιαία ένταση του ρεύματος τη στιγμή αυτή και ποια η χρονική στιγμή t₁;

v)   Να υπολογιστεί η μέση ισχύς του ρεύματος.

vi)   Ο ίδιος αντιστάτης R συνδέεται στο κύκλωμα του διπλανού σχήματος, οπότε σε χρόνο 20s παράγεται πάνω του τόση θερμότητα, όση παράγεται και στο κύκλωμα του εναλλασσόμενου ρεύματος, στον ίδιο χρόνο. Ποιες οι ενδείξεις των δύο οργάνων, τα οποία θεωρούμε ιδανικά;

Απάντηση:

ή

 Ένα παλιό test στο εναλλασσόμενο

 Ένα παλιό test στο εναλλασσόμενο