Ο υπολογισμός της ενεργού έντασης.

Δίνονται οι γραφικές παραστάσεις των εντάσεων σε συνάρτηση με το χρόνο, για τέσσερα ρεύματα τα οποία διαρρέουν έναν αντιστάτη.

i) Ποια ρεύματα θα χαρακτηρίζατε ως συνεχή και ποια ως εναλλασσόμενα;

ii) Να υπολογιστή η ενεργός ένταση κάθε ρεύματος.

Απάντηση:

 ή

Ο υπολογισμός της ενεργού έντασης.

Ο υπολογισμός της ενεργού έντασης.

Εναλλασσόμενη τάση και περιστροφή πλαισίου

Ένα τετράγωνο μεταλλικό πλαίσιο πλευράς α=0,5m  που  δεν εμφανίζει αντίσταση, βρίσκεται κάθετα στις δυναμικές γραμμές ενός ομογενούς μαγνητικού πεδίου έντασης Β=2/π Τ, όπως στο σχήμα.

i)  Πόση είναι η μαγνητική ροή που διέρχεται από το πλαίσιο, θεωρώντας την κάθετη στο πλαίσιο να έχει την κατεύθυνση της έντασης του πεδίου;

ii) Σε μια στιγμή, την οποία θεωρούμε ότι t=0, αρχίζουμε να περιστρέφουμε το πλαίσιο με σταθερή συχνότητα 2Ηz, γύρω από άξονα z, παράλληλο προς την πλευρά ΑΔ, ο οποίος διέρχεται από το κέντρο του.

α) Από ποια εξίσωση παρέχεται η μαγνητική ροή που διέρχεται από το πλαίσιο σε συνάρτηση με το χρόνο; Ποια η τιμή της ροής τη στιγμή t=0,125s;

β) Ποια η τιμή της εναλλασσόμενης τάσης στα άκρα του πλαισίου x και y, τη χρονική στιγμή t=0,125s;

γ) Αν μέσω κατάλληλου συστήματος (δακτύλιοι και ψήκτρες…) συνδέσουμε την παραγόμενη αυτή εναλλασσόμενη τάση, στα άκρα ενός αντιστάτη με R=0,5Ω, να βρείτε την ενεργό ένταση του ρεύματος που θα τον διαρρέει καθώς και την μέση ισχύ του ρεύματος.

Απάντηση:

ή

 Εναλλασσόμενη τάση και περιστροφή πλαισίου

 Εναλλασσόμενη τάση και περιστροφή πλαισίου

Η περιστροφή του πλαισίου και το Ε.Ρ.

Το πλαίσιο του σχήματος αποτελείται από Ν=100 σπείρες όπου η καθεμιά έχει εμβαδόν Α=50cm² και βρίσκεται μέσα σε ένα ομογενές μαγνητικό πεδίο έντασης Β=0,1Τ. Να βρεθούν οι εξισώσεις της μαγνητικής ροής, της τάσης και της έντασης του ρεύματος που διαρρέει τον αντιστάτη με αντίσταση R=10π Ω, σε συνάρτηση με το χρόνο, αν το πλαίσιο στρέφεται με σταθερή γωνιακή ταχύτητα ω=100π rad/s, ενώ τη στιγμή t₀=0, η κάθετη στο πλαίσιο σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία α, όπου:

i) α=0°,    ii)  α=90°,   iii) α=30°.

Θεωρούμε ότι στο κύκλωμα δεν εμφανίζεται άλλη αντίσταση πέρα από αυτή του αντιστάτη.

Απάντηση:

ή

Η περιστροφή του πλαισίου και το Ε.Ρ.

Η περιστροφή του πλαισίου και το Ε.Ρ.

Από πού προέρχεται η ηλεκτρική ενέργεια;

Δίνονται τα παρακάτω σχήματα, όπου στο (α) ένα πλαίσιο μπαίνει σε μαγνητικό πεδίο, κάθετα στις δυναμικές γραμμές με σταθερή ταχύτητα, στο (β) αφήνουμε το μαγνήτη να πέσει κατακόρυφα και πλησιάζει ένα οριζόντιο κυκλικό πλαίσιο και στο (γ) σε μια στιγμή κλείνουμε το διακόπτη.

i) Να εξηγήσετε σε ποιες περιπτώσεις ο αντιστάτης R θα  διαρρέεται από ηλεκτρικό ρεύμα.

ii) Ποια η φορά του επαγωγικού ρεύματος σε κάθε κύκλωμα;

iii) Από πού προέρχεται, σε κάθε περίπτωση, η θερμότητα που αναπτύχθηκε στον αντιστάτη R;

Απάντηση:

ή
 Από πού προέρχεται η ηλεκτρική ενέργεια;

 Από πού προέρχεται η ηλεκτρική ενέργεια;

Ερωτήματα πάνω σε δυο κομμένες εικόνες

Οι όμοιο αγωγοί- ράβδοι ΑΓ και ΔΖ έχουν μάζα 0,4kg, μήκος ℓ= 1m και κινούνται κατακόρυφα σε επαφή με δύο κατακόρυφους στύλους, μέσα σε ένα ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β=0,4Τ. Τη στιγμή που βλέπουμε στο σχήμα, οι αγωγοί πέφτουν με ταχύτητες υ=2m/s, ενώ διαρρέονται από ρεύματα έντασης 2 Α αντίθετης φοράς. Τι υπάρχει στην κορυφή των κατακόρυφων αγωγών και τι άλλο περιέχει κάθε κύκλωμα, δεν το βλέπουμε.

i)   Να υπολογιστεί η ηλεκτρεγερτική δύναμη που αναπτύσσεται σε κάθε αγωγό τη στιγμή αυτή και να βρεθεί η ισχύς της.

ii) Να βρεθεί η επιτάχυνση την οποία έχει κάθε ράβδος.

iii) Να υπολογιστεί η ισχύς κάθε δύναμης που ασκείται στις ράβδους.

iv) Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου.

Δίνεται g=10m/s².

Απάντηση:

ή

 Ερωτήματα πάνω σε δυο κομμένες εικόνες

 Ερωτήματα πάνω σε δυο κομμένες εικόνες

Δύο δεύτερα στον ηλεκτρομαγνητισμό.

1. Περιστροφή πηνίου

Το πηνίο του σχήματος αποτελείται από 100 σπείρες, που η κάθε μία έχει εμβαδόν S=10cm² και αντίσταση R_σπ.=0,04Ω. Το πηνίο συνδέεται με βαλιστικό γαλβανόμετρο αντίστασης R_G=2Ω. Το σύστημα βρίσκεται σε ομογενές μαγνητικό πεδίο με το επίπεδο των σπειρών κάθετο στις μαγνητικές γραμμές. Αν με περιστροφή του πηνίου κατά 90^ο (ώστε το επίπεδο των σπειρών να γίνει παράλληλο με τις γραμμές), από το γαλβανόμετρο διέρχεται φορτίο 0,05C τότε το μέτρο του μαγνητικού πεδίουείναι:

α. B=5T                       β. B=2T                        γ. B=3T

Επιλέξτε την απάντησή σας.

Δικαιολογήστε την επιλογή σας.

Η φορά της καθέτου στον δακτύλιο φαίνεται στο σχήμα 1.

Συνέχεια

Οι δύο όψεις της επαγωγής

Η ράβδος ΑΓ μήκους ℓ=1m και μάζας m=0,5kg μπορεί να κινείται χωρίς τριβές, σε επαφή με τους οριζόντιους αγωγούς xx΄ και yy΄ παραμένοντας συνεχώς κάθετη σε αυτούς. Τα άκρα x και y των αγωγών συνδέονται μέσω ενός αντιστάτη με αντίσταση R=0,2Ω, ενώ η ράβδος και οι αγωγοί xx΄ και  yy΄ δεν παρουσιάζουν αντίσταση. Κάποια στιγμή t_ο=0 στον χώρο δημιουργείται ομογενές μαγνητικό πεδίο έντασης B, με φορά όπως στο σχήμα, το μέτρο της οποίας μεταβάλλεται όπως στο δεύτερο σχήμα.

i) Για το χρονικό διάστημα από 0 έως τη στιγμή t₁=2,5s, να υπολογιστούν:

α)  Η απαραίτητη οριζόντια δύναμη F₁ που πρέπει να ασκούμε στην ράβδο ΑΓ, ώστε να μην μετακινηθεί, παραμένοντας στην θέση της, και να κάνετε τη γραφική της παράσταση σε συνάρτηση με το χρόνο, αν δίνεται η απόσταση (xΑ)=d=0,8m.

β) Η ενέργεια που μεταφέρεται στη ράβδο μέσω της παραπάνω δύναμης F₁, καθώς και το αντίστοιχο έργο της ασκούμενης, από το μαγνητικό πεδίο στη ράβδο, δύναμης Laplace.

γ)  Η ηλεκτρική ενέργεια που εμφανίζεται στο κύκλωμα.

ii) Τη χρονική στιγμή t₁ ασκούμε στο μέσον της ράβδου μια σταθερή οριζόντια δύναμη με φορά προς τα  δεξιά, μέτρου F₂=2Ν, με αποτέλεσμα μετά από λίγο, τη στιγμή t₂ η ράβδος να έχει ταχύτητα υ₂=2m/s. Για τη στιγμή αυτή να υπολογιστούν:

α) Ο  ρυθμός με τον οποίο μεταφέρεται ενέργεια στη  ράβδο, μέσω του έργου της δύναμης F₂, καθώς και η αντίστοιχη ισχύς της δύναμης Laplace.

β) Η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα, καθώς και ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου.

Απάντηση:

ή

 Οι δύο όψεις της επαγωγής

 Οι δύο όψεις της επαγωγής

Η οριακή ταχύτητα και το κλείσιμο του διακόπτη

Ο αγωγός ΚΛ αφήνεται να κινηθεί κατακόρυφα, σε επαφή με δύο κατακόρυφους στύλους Ax και Γy, όπως στο σχήμα, τη στιγμή t_o=0. Οι δύο στύλοι συνδέονται στα πάνω άκρα τους με αντίσταση R, ενώ το σύστημα βρίσκεται εντός ενός οριζόντιου ομογενούς μαγνητικού πεδίου, έντασης Β.

i)  Ο αγωγός θα κινηθεί με μεταβλητή επιτάχυνση με τιμές από g έως μηδέν.

ii) Αν τη στιγμή t₁ που ο αγωγός έχει αποκτήσει την οριακή του ταχύτητα υ₁ (έχοντας μηδενική επιτάχυνση), κλείσουμε το διακόπτη δ, οπότε παρεμβάλλεται και μια ακόμη αντίσταση R, τότε ο ΚΛ θα αποκτήσει στιγμιαία επιτάχυνση με φορά προς τα πάνω και μέτρο g.

iii) Αν τελικά ο αγωγός ΚΛ αποκτήσει ξανά οριακή ταχύτητα, πριν φτάσει στα άκρα x,y των στύλων, αυτή θα έχει ξανά μέτρο υ₁.

Να χαρακτηρίστε τις προτάσεις αυτές ως σωστές ή λανθασμένες, δικαιολογώντας αναλυτικά τις απαντήσεις σας

Δίνεται ότι g είναι η επιτάχυνση της βαρύτητας και ότι ο αγωγός ΚΛ και οι δύο κατακόρυφοι στύλοι δεν έχουν αντίσταση.

Απάντηση:

ή

 Η οριακή ταχύτητα και το κλείσιμο του διακόπτη

 Η οριακή ταχύτητα και το κλείσιμο του διακόπτη

Η επιβράδυνση του αγωγού στο μαγνητικό πεδίο

Ο αγωγός ΔΖ μάζας m=0,5kg και μήκους ℓ=1m, κινείται οριζόντια σε επαφή με δυο παράλληλους αγωγούς ΑΑ₁ και ΓΓ₁ μήκους d=5m, χωρίς τριβές, μέσα σε ένα ομογενές κατακόρυφο μαγνητικό πεδίο έντασης Β=0,5Τ, το οποίο εκτείνεται στην περιοχή που ορίζεται από τους αγωγούς ΑΑ₁ και ΓΓ₁. Ο αγωγός ΔΖ και οι δύο αγωγοί ΑΑ₁ και ΓΓ₁ δεν παρουσιάζουν αντίσταση, ενώ μεταξύ των άκρων Α και Γ συνδέεται αντιστάτης με αντίσταση R=0,5Ω. Σε μια στιγμή t₀=0, ο αγωγός ΔΖ απέχει κατά x_ο=0,5m από τα άκρα ΑΓ και έχει ταχύτητα υ_ο=4m/s παράλληλη προς τον αγωγό ΑΑ₁ με φορά προς τα δεξιά. Η ταχύτητα αυτή είναι επίσης κάθετη στον αγωγό ΔΖ. Με την επίδραση κατάλληλης οριζόντιας δύναμης F, κάθετης προς τον ΔΖ, επιτυγχάνουμε ο αγωγός να επιβραδύνεται, έχοντας  σταθερή επιτάχυνση, με φορά αντίθετη της ταχύτητας και μέτρο α=2m/s², μέχρι τη θέση που μηδενίζεται η ταχύτητά του, όπου και σταματά να ασκείται πάνω του και η δύναμη F.

i)   Να υπολογιστεί η μέγιστη τιμή της μαγνητικής ροής που διέρχεται από το ορθογώνιο ΑΔΖΓ, θεωρώντας την κάθετη στην επιφάνεια να έχει την ίδια φορά με την ένταση του πεδίου.

ii)  Να βρεθεί η συνάρτηση της μαγνητικής ροής που περνά από το παραπάνω ορθογώνιο, σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση.

iii) Να βρεθεί η εξίσωση της έντασης του ρεύματος που διαρρέει τον αγωγό ΔΖ, σε συνάρτηση με το χρόνο και να υπολογιστεί ο ρυθμός με τον οποίο παράγεται θερμότητα στον αντιστάτη τις χρονικές στιγμές:

α) t₁=0,5s,   β) t₂=1s και  γ)  t₃=1,5s.

 iv) Πόση είναι η ισχύς της δύναμης Laplace τις παραπάνω χρονικές στιγμές και ποια η αντίστοιχη ισχύς της δύναμης F;

Απάντηση:

ή

Η επιβράδυνση του αγωγού στο μαγνητικό πεδίο

Η επιβράδυνση του αγωγού στο μαγνητικό πεδίο

Επαγόμενο φορτίο

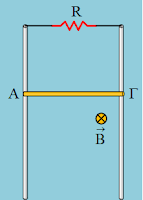
 Ένας μαγνήτης περνά μέσα από ένα δακτύλιο και κατόπιν μέσα από ένα σύρμα με δύο όμοια κυκλικά τυλίγματα με αυτά του μονού δακτυλίου, όπως φαίνεται στο σχήμα 1. Ο μαγνήτης και στις δύο περιπτώσεις κινείται με ίδια ταχύτητα και με κατάλληλο τρόπο φροντίζουμε να είναι σταθερή. Ο μονός δακτύλιος και το σύρμα είναι από το ίδιο υλικό και έχουν και ίδιο πάχος, (διατομή).

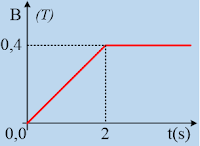
i) Για τις απόλυτες μέσες τιμές της επαγωγικής τάσης Ε₁ (αγνοώντας την αλλαγή της φοράς του ρεύματος) που αναπτύσσεται όταν ο μαγνήτης περνά από τον μονό δακτύλιο και Ε₂ όταν περνά από τον διπλό αντίστοιχα, ισχύει:

α. Ε₂=Ε₁          β. Ε₁=Ε₂/2        γ. Ε₂=2Ε₁

ii) Αν το συνολικό επαγόμενο φορτίο ανεξαρτήτου φοράς του ρεύματος, στο μονό δακτύλιο είναι Q₁ και στους δύο δακτύλιους Q₂ αντίστοιχα, τότε ισχύει:

α. Q₂=2Q₁                   β. Q₁=Q₂/2                   γ. Q₂=Q₁

Η φορά της καθέτου στον δακτύλιο φαίνεται στο σχήμα 1.

Απάντηση

Η επαγωγή κατά μια επιταχυνόμενη κίνηση.

 Ο αγωγός ΚΛ του σχήματος, μάζας 0,5kg και μήκους ℓ=1m, μπορεί να κινείται οριζόντια, σε επαφή με δυο παράλληλους αγωγούς Αx και Γy χωρίς τριβές, μέσα σε ένα ομογενές κατακόρυφο μαγνητικό πεδίο έντασης Β, το οποίο εκτείνεται στην περιοχή που ορίζεται από τους αγωγούς Αx και Γy. Ο αγωγός ΚΛ και οι δύο αγωγοί Αx και Γy δεν παρουσιάζουν αντίσταση, ενώ μεταξύ των άκρων Α και Γ συνδέεται αντιστάτης με αντίσταση R=0,32Ω. Ο αγωγός ΚΛ βρίσκεται ακίνητος, όπως στο σχήμα απέχοντας κατά (ΑΚ)=(ΓΛ)=x_ο=0,2m από τα άκρα Α και Γ των παραλλήλων αγωγών. 

Σε μια στιγμή t=0, ο αγωγός ΚΛ δέχεται την επίδραση κατάλληλης οριζόντιας (εξωτερικής) δύναμης F, κάθετης στον αγωγό, με αποτέλεσμα να αποκτά σταθερή επιτάχυνση και να κινείται προς τα δεξιά. Στο διάγραμμα φαίνεται η μαγνητική ροή που διέρχεται από την επιφάνεια του ορθογωνίου ΑΚΛΓ σε συνάρτηση με το χρόνο.  

i)  Να βρεθεί η ένταση του μαγνητικού πεδίου Β, καθώς και η απόσταση d του άκρου Κ του αγωγού ΚΛ από το σημείο Α τη στιγμή t₁=2s.

ii) Να αποδειχθεί ότι στο ορθογώνιο ΑΚΛΓ αναπτύσσεται ηλεκτρεγερτική δύναμη από επαγωγή, ανάλογη του χρόνου και να βρεθεί η τιμή της τη στιγμή t₁. 

iii) Να υπολογιστεί το συνολικό φορτίο που περνά από 0-t₁ από μια διατομή του αγωγού ΚΛ.

iv) Να γίνουν οι γραφικές παραστάσεις σε συνάρτηση με το χρόνο, από 0-t₁ των μεγεθών:

α) ΗΕΔ από επαγωγή,

β) ένταση ρεύματος,

γ) Δύναμη Laplace που ασκείται στον αγωγό ΚΛ.

δ) Ασκούμενης (εξωτερικής) δύναμης F.

Δίνεται ότι η προς τα δεξιά κατεύθυνση, θεωρείται θετική, όπως επίσης ότι η κάθετος στην επιφάνεια του ορθογωνίου ΑΚΛΓ έχει την κατεύθυνση της έντασης του μαγνητικού πεδίου.

Απάντηση:

ή

Η επαγωγή κατά μια επιταχυνόμενη κίνηση.

Η επαγωγή κατά μια επιταχυνόμενη κίνηση.

Όταν την οριακή ταχύτητα την αποκτά αγωγός

 Ο αγωγός ΚΛ μήκους ℓ=0,4m, ισορροπεί στη θέση που δείχνεται στο σχήμα, σε επαφή με δύο κατακόρυφους αγωγούς Αx και Γy, οι οποίοι στα άνω άκρα τους συνδέονται μέσω αντίστασης R=0,2Ω. Το σύστημα βρίσκεται μέσα σε ένα ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β=2Τ, κάθετης στο επίπεδο των αγωγών, με την επίδραση μιας κατακόρυφης δύναμης F, μέτρου F_ο=2Ν. Σε μια στιγμή αυξάνουμε το μέτρο της ασκούμενης δύναμης στην τιμή F=5Ν, με αποτέλεσμα ο αγωγός ΑΚ να αρχίσει να επιταχύνεται προς τα πάνω.

i)  Να βρείτε την ηλεκτρεγερτική δύναμη που αναπτύσσεται στον αγωγό ΚΛ, σε συνάρτηση με την ταχύτητά του.

ii) Σε μια  στιγμή t₁ ο ΚΛ έχει ταχύτητα υ₁=0,5m/s. Για τη στιγμή αυτή να βρεθούν:

α)  Η ένταση του ρεύματος που διαρρέει τον αγωγό και η επιτάχυνσή του.

β)  Η ισχύς κάθε δύναμης που ασκείται στον αγωγό ΚΛ.

γ)  Η ηλεκτρική ισχύς που εμφανίζεται στο κύκλωμα, καθώς και οι ρυθμοί μεταβολής της κινητικής ενέργειας, της δυναμικής ενέργειας και της μηχανικής ενέργειας του αγωγού ΚΛ.

iii) Να αποδείξτε ότι ο αγωγός θα αποκτήσει, μετά από λίγο, σταθερή (οριακή) ταχύτητα, την οποία και να υπολογίσετε, με δεδομένο ότι η οριακή ταχύτητα αποκτάται, πριν ο αγωγός φτάσει στα άνω άκρα των στύλων.

Δίνεται ότι ο αγωγός ΚΛ καθώς και οι κατακόρυφοι αγωγοί δεν παρουσιάζουν αντίσταση, ενώ g=10m/s².

Απάντηση:

ή

 Όταν την οριακή ταχύτητα την αποκτά αγωγός

 Όταν την οριακή ταχύτητα την αποκτά αγωγός

Όταν το πλαίσιο αποκτά οριακή ταχύτητα

Όταν το πλαίσιο αποκτά οριακή ταχύτητα

Το τετράγωνο μεταλλικό πλαίσιο ΑΒΓΔ με πλευρά l=0,4m και αντίσταση R=0,2Ω, ισορροπεί στη θέση που δείχνεται στο σχήμα, με την πάνω πλευρά του ΑΒ στα όρια ενός ομογενούς οριζόντιου μαγνητικού πεδίου έντασης Β=2Τ, κάθετης στο επίπεδο του πλαισίου, με την επίδραση μιας κατακόρυφης δύναμης F, μέτρου F_ο=2Ν. Σε μια στιγμή αυξάνουμε το μέτρο της ασκούμενης δύναμης στην τιμή F=5Ν, με αποτέλεσμα το πλαίσιο να αρχίσει να επιταχύνεται προς τα πάνω, μπαίνοντας στο μαγνητικό πεδίο.

i)  Να βρείτε την ηλεκτρεγερτική δύναμη που αναπτύσσεται στο πλαίσιο, σε συνάρτηση με την ταχύτητα του πλαισίου.

ii) Σε μια  στιγμή t₁ το πλαίσιο έχει ταχύτητα υ₁=0,5m/s. Για τη στιγμή αυτή να βρεθούν:

α)  Η ένταση του ρεύματος που διαρρέει το πλαίσιο και η επιτάχυνσή του.

β)  Η ισχύς κάθε δύναμης που ασκείται στο πλαίσιο.

γ)  Η ηλεκτρική ισχύς που εμφανίζεται στο πλαίσιο, καθώς και οι ρυθμοί μεταβολής της κινητικής ενέργειας, της δυναμικής ενέργειας και της μηχανικής ενέργειας του πλαισίου.

iii) Να αποδείξτε ότι το πλαίσιο θα αποκτήσει, μετά από λίγο, σταθερή (οριακή) ταχύτητα, την οποία και να υπολογίσετε, με δεδομένο ότι η απόκτηση της οριακής ταχύτητας αποκτάται, πριν την είσοδο της πλευράς ΓΔ στο πεδίο.

Δίνεται g=10m/s².

Απάντηση:

ή
Όταν το πλαίσιο αποκτά οριακή ταχύτητα

Όταν το πλαίσιο αποκτά οριακή ταχύτητα

Ο αγωγός πέφτει κατακόρυφα

Ο αγωγός ΑΓ του σχήματος έχει μάζα 0,1kg, μήκος ℓ=1m και αντίσταση r=1Ω. Σε μια στιγμή ο αγωγός αφήνεται να κινηθεί σε επαφή με δύο κατακόρυφους στύλους, μέσα σε ένα οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=0,5Τ, όπως στο σχήμα. Τα πάνω άκρα των  δύο στύλων συνδέονται μέσω αντίστασης R. Μετά από λίγο, τη στιγμή t₁, ο αγωγός ΑΓ έχει αποκτήσει ταχύτητα υ=2m/s, ενώ ο αντιστάτης διαρρέεται από ρεύμα έντασης i=0,5Α. Για τη στιγμή αυτή να βρεθούν:

i)  Ο ρυθμός μεταβολής της μαγνητικής ροής που διέρχεται από την επιφάνεια του ορθογωνίου που σχηματίζεται, καθώς και η ηλεκτρεγερτική δύναμη που αναπτύσσεται στο κύκλωμα. Θεωρείστε την κάθετη στην επιφάνεια να έχει φορά προς τα μέσα, ίδια με την ένταση του μαγνητικού πεδίου.

ii) Η φορά της έντασης του ρεύματος που διαρρέει τον αγωγό ΑΓ.

iii) Η επιτάχυνση του αγωγού ΑΓ και ο ρυθμός μεταβολής της κινητικής του ενέργειας.

iv) Η ισχύς της ΗΕΔ από επαγωγή. Τι ποσοστό της παραπάνω ισχύος απορροφά ο αντιστάτης R;

v) Τι ενεργειακές μεταβολές εμφανίζονται στο κύκλωμα την παραπάνω στιγμή;

Οι κατακόρυφοι στύλοι δεν εμφανίζουν αντίσταση, ενώ g=10m/s².

Απάντηση:

ή

 Ο αγωγός πέφτει κατακόρυφα

 Ο αγωγός πέφτει κατακόρυφα