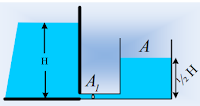
Θέλουμε να αντλήσουμε νερό από μια υπερυψωμένη δεξαμενή,
μέσω ενός σωλήνα-λάστιχου και να γεμίσουμε δύο δοχεία, ίδιου όγκου. Αυτό μπορούμε
να το κάνουμε, με τους τρόπους που περιγράφονται στο διπλανό σχήμα.
Για το Α δοχείο, χρησιμοποιούμε ένα κοντό λάστιχο,
μετακινώντας το κάτω άκρο του, ώστε να βρίσκεται διαρκώς στην επιφάνεια του
νερού στο δοχείο. Με τον τρόπο αυτό, για να γεμίσουμε το δοχείο απαιτείται χρόνος
t1= 50s.
 Το δοχείο Β, το γεμίζουμε χρησιμοποιώντας ένα όμοιο αλλά
μακρύτερο λάστιχο, προσέχοντας το άκρο του να ακουμπά συνεχώς στη βάση του δοχείου.
Το δοχείο Β, το γεμίζουμε χρησιμοποιώντας ένα όμοιο αλλά
μακρύτερο λάστιχο, προσέχοντας το άκρο του να ακουμπά συνεχώς στη βάση του δοχείου.
i) Αν η ροή του νερού, θεωρηθεί ροή ιδανικού
ρευστού, τότε για να γεμίσει το δοχείο Β, θα απαιτηθεί χρονικό διάστημα:
α) t2=40s,
β) t2=50s,
γ) t2=60s.
ii)
Στην πραγματικότητα βέβαια το νερό δεν είναι ιδανικό ρευστό αλλά πραγματικό! Τότε
για να γεμίσει το Β δοχείο θα απαιτηθεί χρονικό διάστημα:
α) t2=40s, β) t2=50s, γ) t2=60s.
ή
 |