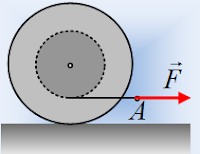
Σε ένα κύλινδρο μάζας Μ και ακτίνας R , ασκούμε μεσω κατάλληλου μηχανισμού μία σταθερή δύναμη F στο κέντρο μάζας του. Ο κύλινδρος βρίσκεται αρχικά στο σημείο Α πάνω σε τραχύ έδαφος όπου στα μέσα της διαδρομής (σημείο Β) γίνεται τελείως λείο. Η τριβή είναι αρκετή ώστε να αρχίσει (με την άσκηση της δύναμης F) κύλιση χωρίς ολίσθηση. Στο τέλος της διαδρομής (σημείο Γ) έχει αποκτήσει ολική κινητική ενέργεια Κ1. Επαναλαμβάνουμε την διαδικασία από το σημείο Γ (με υΓ = 0) προς το Α, ασκώντας την ίδια οριζόντια δύναμη F στο κέντρο του κυλίνδρου αλλά με κατεύθυνση προς το σημείο Α. Στο τέλος της διαδρομής (σημείο Α) η ολική κινητική ενέργεια του κυλίνδρου είναι Κ2. Για τις κινητικές ενέργειες στι δύο περιπτώσεις ισχύει:
α. Κ1 > Κ2 β. Κ1 = Κ2 γ. Κ1 < Κ2
Να επιλέξετε την σωστή και να αιτιολογήσετε την απάντηση σας.