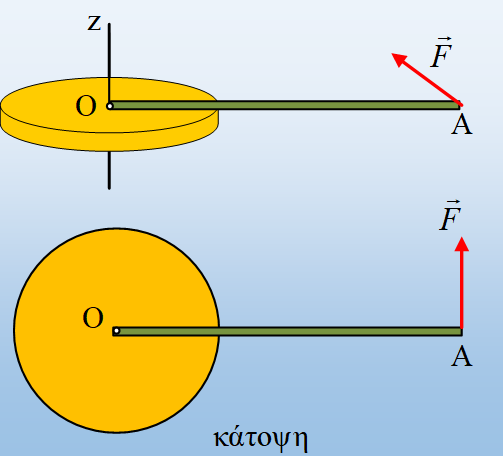
Ο οριζόντιος ομογενής δίσκος μπορεί να περιστρέφεται, χωρίς τριβές γύρω από κατακόρυφο άξονα z, ο οποίος περνά από το κέντρο του Ο. Γύρω από τον ίδιο άξονα μπορεί να στρέφεται, επίσης χωρίς τριβές και η ομογενής ράβδος ΟΑ, μάζας m=6kg και μήκους ℓ=2m, η οποία στηρίζεται πάνω στο δίσκο. Το σύστημα ηρεμεί.
Κάποια στιγμή t=0 ασκούμε στο άκρο Α της ράβδου μια σταθερού μέτρου δύναμη F=5Ν, η οποία αρχίζει να περιστρέφει τη ράβδο, παραμένοντας διαρκώς κάθετη σε αυτήν, όπως στο σχήμα (το κάτω σε κάτοψη). Εξαιτίας της τριβής η οποία αναπτύσσεται μεταξύ ράβδου και δίσκου, ο δίσκος αρχίζει και αυτός να στρέφεται γύρω από τον άξονα z. Αν ο ρυθμός μεταβολής της στροφορμής της ράβδου ως προς τον άξονα z έχει μέτρο 8kg∙m2/s2, ζητούνται:
i) Να σχεδιαστεί στο σχήμα το διάνυσμα του ρυθμού μεταβολής της στροφορμής της ράβδου και να υπολογιστεί η ροπή της τριβής που ασκείται στη ράβδο, από τον δίσκο.
ii) Ο ρυθμός μεταβολής της στροφορμής του συστήματος ως προς τον άξονα z, καθώς και ο αντίστοιχος, ρυθμός μεταβολής της στροφορμής του δίσκου, ως προς τον ίδιο άξονα.
iii) Η στροφορμή ως προς τον άξονα z, τη χρονική στιγμή t1=5s:
α) της ράβδου, β) του δίσκου.
iv) Αν η ροπή αδράνειας του δίσκου ως προς τον άξονα z έχει τιμή Ιδ=2,5kgm2, να υπολογιστούν:
α) Η κινητική ενέργεια του δίσκου τη στιγμή t1.
β) Η μηχανική ενέργεια που μετατρέπεται σε θερμική από 0-t1 εξαιτίας της τριβής.
Για τη ράβδο Ιcm= mℓ2/12.
ή

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.