Το φετινό μας διαγώνισμα στις ταλαντώσεις (2021)

Ένα σώμα Σ₁, μάζας m₁ = 1 kg, μπορεί να κινείται χωρίς τριβές σε λείο οριζόντιο επίπεδο. Το Σ₁ είναι δεμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς k₁ = 100 N/m, με το αριστερό άκρο του να είναι στερεωμένο σε ακλόνητο κατακόρυφο τοίχο. Σε απόσταση d₁ από τη θέση ισορροπίας του Σ₁ και δεξιά αυτής, βρίσκεται ένα ακίνητο σώμα Σ_2, μάζας m_2, το οποίο μπορεί να κινείται και αυτό στο ίδιο επίπεδο χωρίς τριβές. Δεξιά του σώματος Σ₂ και σε απόσταση d₂ βρίσκεται το ελεύθερο άκρο οριζοντίου ιδανικού ελατηρίου σταθεράς k₂ που έχει  το δεξιό  του άκρο στερεωμένο σε σώμα Σ₃, μάζας m₃. Το Σ₃ παρουσιάζει τριβή με το οριζόντιο δάπεδο. Ασκώντας στο σώμα Σ₁ κατάλληλη δύναμη συμπιέζουμε το ελατήριο σταθεράς k₁ κατά d και στη συνέχεια το αφήνουμε ελεύθερο να εκτελέσει απλή αρμονική ταλάντωση. Μετά από χρονικό διάστημα Δt₁ = π/15 s από τη στιγμή που ελευθερώσαμε το σώμα Σ₁, αυτό συγκρούεται κεντρικά και ελαστικά με το  σώμα Σ₂, με αποτέλεσμα το Σ₁  αμέσως μετά την κρούση να αρχίσει μία νέα ταλάντωση με μηδενική ταχύτητα. Το  σώμα Σ₂ μετά την ελαστική κρούση και αφού διανύσει διάστημα d₂, προσπίπτει στο ελεύθερο άκρο του ελατηρίου σταθεράς k₂. Η στατική τριβή που αναπτύσσεται μεταξύ δαπέδου και σώματος  Σ₃ το κρατά ακίνητο και το μέτρο της μεγιστοποιείται για πρώτη φορά αφού περάσει χρονικό διάστημα Δt₂ = π/40 s  μετά την εμφάνισή της. Η γραφική παράσταση της στατικής τριβής φαίνεται στο σχήμα. 

  Δ1. Να βρείτε τη μάζα του σώματος Σ₂ καθώς και το μέτρο της μέγιστης δύναμη που ασκεί το ελατήριο σταθεράς k₂ κατά την συμπίεσή του. 

Δ2. Τη μέγιστη συσπείρωση του ελατηρίου σταθεράς k₂. 

Δ3. Να υπολογίσετε την ταχύτητα υ₁ του σώματος Σ₁ ελάχιστα πριν την κρούση με το Σ_2. 

Δ4. Να γράψετε την εξίσωση της ταλάντωσης του σώματος Σ₁ μετά την κρούση του με το Σ₂, θεωρώντας ως t′ = 0 την στιγμή έναρξης της νέας ταλάντωσης. 

Δ5.  Να υπολογίστε την απόσταση d₂ ώστε τα σώματα να ξανασυγκρουσθούν στη θέση ισορροπίας του Σ₁ , όταν αυτό διέρχεται από αυτήν για 2^η φορά μετά το χάσιμο της επαφής. 

Το διαγώνισμα εδώ. 

 Το φετινό διαγώνισμα για τα ΨΕΒ που εκπονήσαμε εγώ και ο Πρόδρομος. Τα θέματα διαφέρουν λίγο από την αρχική δομή που έτυχε να δουν κάποιοι φίλοι, αλλά έτσι είναι η διαδικασία. Οι λύσεις προφανώς και υπάρχουν αλλά δεν μπορούν να δημοσιευθούν πριν από την επίσημη ανάρτησή τους στα ΨΕΒ.

Ο κλειστός και ο ανοικτός σωλήνας σε μια ροή

  

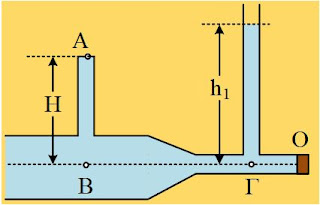
Στο σχήμα βλέπουμε ένα τμήμα δικτύου, το δεξιό άκρο Ο του οποίου κλείνεται με τάπα. Στον κεντρικό σωλήνα με μεταβλητή διατομή, έχουν προσαρμοσθεί δύο κατακόρυφοι λεπτοί σωλήνες, ο πρώτος κλειστός γεμάτος νερό, με ύψος Η=0,6m (από τον άξονα του σωλήνα), ενώ ο δεύτερος ανοικτός, όπου το νερό ανεβαίνει σε ύψος h₁=0,8m (ξανά από τον άξονα του οριζόντιου σωλήνα). Η διατομή του σωλήνα στην περιοχή του σημείου Γ είναι Α₁=1cm², ενώ στην περιοχή του σημείου Β η αντίστοιχη διατομή είναι τετραπλάσια.

i) Να υπολογιστεί η δύναμη που ασκεί το νερό στην τάπα.

ii) Να βρεθεί η πίεση στο σημείο Α, στο πάνω μέρος του κλειστού σωλήνα.

iii) Ανοίγουμε την τάπα και αποκαθίσταται μια μόνιμη ροή, όπου το νερό εξέρχεται από το άκρο Ο με ταχύτητα υ=4m/s. Παρατηρούμε τώρα η στάθμη στον ανοικτό σωλήνα να έχει κατέβει κατά 20cm.

α)  Υποστηρίζεται ότι η διατομή της φλέβας αμέσως μετά την έξοδο, από το σωλήνα, είναι μικρότερη από την διατομή Α₁ του σωλήνα. Μπορείτε με βάση τα παραπάνω δεδομένα να ελέγξετε την ορθότητα ή όχι της παραπάνω πρότασης;

β) Σε πόσο χρόνο μπορούμε να γεμίσουμε με νερό, ένα δοχείο με όγκο V=4L, από το παραπάνω δίκτυο;

γ) Να υπολογίσετε ξανά την πίεση στο σημείο Α του κλειστού σωλήνα.

Δίνεται η πυκνότητα του νερού, το οποίο θεωρείται ιδανικό ρευστό ρ=1.000kg/m³ και η επιτάχυνση της βαρύτητας g=10m/s². Στο σχήμα δεν "κρατήθηκαν" οι σωστές διαστάσεις...

Απάντηση:

ή

 Ο κλειστός και ο ανοικτός σωλήνας σε μια ροή

 Ο κλειστός και ο ανοικτός σωλήνας σε μια ροή

Δυνάμεις στις πλευρές του κύβου

 

Ένα σώμα κυβικού σχήματος με ακμή α=0,5m και βάρους w=2.000Ν βυθίζεται σε μια μεγάλη δεξαμενή νερού, δεμένο στο κάτω άκρο ενός νήματος, το οποίο έχει προσδεθεί σε σταθερό σημείο, όπως στο σχήμα, με αποτέλεσμα η πάνω βάση του κύβου να είναι οριζόντια. Αν η βάση αυτή δέχεται δύναμη μέτρου F₁=28.000Ν, να υπολογιστούν:

i)  Η δύναμη που το νερό ασκεί στην κάτω βάση του κύβου.

ii) Το μέτρο της δύναμης που ασκείται από το νερό σε μια παράπλευρη έδρα του κύβου.

iii) Η τάση του νήματος, από το οποίο κρέμεται ο κύβος.

Δίνεται η πυκνότητα του νερού ρ=1.000kg/m³ και g=10m/s², ενώ δεν είναι γνωστή η ατμοσφαιρική πίεση που επικρατεί στην περιοχή της δεξαμενής!

Απάντηση:

ή

 Δυνάμεις στις πλευρές του κύβου

 Δυνάμεις στις πλευρές του κύβου

Δυο τάπες σε ένα σωλήνα

 

  

Ένα ανοικτό δοχείο περιέχει νερό μέχρι ύψος Η=1m. Κοντά στον πυθμένα του έχει συνδεθεί ένας κατακόρυφος λεπτός σωλήνας ύψους h=1,5m, κλειστός στο πάνω του άκρο Β με τάπα, εμβαδού Α=2cm². Στο ίδιο ύψος με την ελεύθερη επιφάνεια του νερού  στο δοχείο, στη θέση Γ, ο λεπτός σωλήνας έχει μια οπή η οποία είναι κλεισμένη με μια δεύτερη τάπα, ίδιου εμβαδού, όπως στο σχήμα. Στον σωλήνα δεν έχει εγκλωβιστεί αέρας.

i)  Να υπολογιστούν η πίεση στο πάνω μέρος του λεπτού σωλήνα, καθώς και οι δυνάμεις που το νερό ασκεί στις δύο τάπες.

ii) Αν αφαιρέσουμε την τάπα στο άκρο Β, τι πρόκειται να συμβεί;

iii) Αν με κλειστή την τάπα στο Β, ανοίξουμε την τάπα στο σημείο Γ, τι θα συμβεί;

iv) Τι θα συμβεί, αν ανοίξουμε ταυτόχρονα τις δύο τάπες;

Δίνεται η ατμοσφαιρική πίεση p_ατμ=10⁵Ρα, η πυκνότητα του νερού ρ=1.000kg/m³ και g=10m/s².

Απάντηση:

ή

  Δυο τάπες σε ένα σωλήνα

  Δυο τάπες σε ένα σωλήνα

Η εξωτερική δύναμη σε μια εξαναγκασμένη ταλάντωση.

Μια πλάκα μάζας m, εκτελεί εξαναγκασμένη κατακόρυφη ταλάντωση στο κάτω άκρο ενός ιδανικού ελατηρίου σταθεράς k=100∙m (S.Ι.), με την επίδραση μιας περιοδικής εξωτερικής δύναμης F_εξ, ενώ πάνω της ασκείται δύναμη απόσβεσης της μορφής F_απ=-bυ, Μετά το πέρας των μεταβατικών φαινομένων, λαμβάνοντας κάποια στιγμή ως αρχή μέτρησης των χρόνων t=0, η εξίσωση της απομάκρυνσης ικανοποιεί την εξίσωση x=Α∙ημ(8t) (S.Ι.), με θετική κατεύθυνση προς τα πάνω.

i) Κάποια στιγμή t₁ η πλάκα περνά από την θέση x=0, κινούμενη προς τα κάτω.

Α) Τη στιγμή αυτή η ισχύς της εξωτερικής δύναμης Ρ₁ είναι:

α) Αρνητική,  β) Μηδέν,   γ) Θετική.

Β) Η παραπάνω ισχύς της εξωτερικής δύναμης είναι ανάλογη:

α) του τετραγώνου της ιδιοσυχνότητας ταλάντωσης,

β) του πλάτους ταλάντωσης,

γ) της σταθεράς απόσβεσης b.

Ποιες από τις παραπάνω προτάσεις είναι σωστές;

ii) Μια άλλη στιγμή t₂ η πλάκα βρίσκεται στην άνω ακραία θέση της ταλάντωσής της. Τη στιγμή αυτή η εξωτερική δύναμη:

α) Είναι μηδενική.

β) Έχει κατεύθυνση προς τα κάτω.

γ) Έχει κατεύθυνση προς τα πάνω.

Απάντηση:

ή

 Η εξωτερική δύναμη σε μια εξαναγκασμένη ταλάντωση.

 Η εξωτερική δύναμη σε μια εξαναγκασμένη ταλάντωση.

Ενέργειες και επιτάχυνση στην φθίνουσα ταλάντωση

  

Μια πλάκα μάζας m ηρεμεί στο κάτω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k, όπως στο σχήμα, στη θέση Ο. Ανεβάζουμε το σώμα κατακόρυφα κατά d=2mg/k, φέρνοντάς στη θέση (1) και κάποια στιγμή το αφήνουμε να κινηθεί, χωρίς να του προσδώσουμε κάποια αρχική ταχύτητα. Η πλάκα ταλαντώνεται δεχόμενη δύναμη απόσβεσης της μορφής F_α=-bυ.

i) Η μέγιστη δυναμική ενέργεια του ελατηρίου στη διάρκεια της ταλάντωσης, έχει τιμή:

α) U_ελ,mαx=m²g²/2k,    β) m²g²/2k <  U_ελ,mαx< 9m²g²/2k, γ) U_ελ,mαx=9m²g²/2k

ii)  Η μέγιστη κινητική ενέργεια την οποία αποκτά το σώμα, στη διάρκεια της ταλάντωσής του έχει τιμή:

α)  Κ_mαx < 2m²g²/k,    β) Κ_mαx = 2m²g²/k,   γ) Κ_mαx > 2m²g²/k

iii) Κάποια στιγμή η πλάκα περνάει από την θέση Ο με ταχύτητα μέτρου υ₁, με φορά προς τα πάνω. Τη στιγμή αυτή:

α) Έχει επιτάχυνση με φορά προς τα πάνω.

β) Έχει επιτάχυνση με φορά προς τα κάτω.

γ) Δεν έχει επιτάχυνση.

Να δικαιολογήσετε τις απαντήσεις  σας.

Απάντηση:

ή

  Ενέργειες και επιτάχυνση  στην φθίνουσα ταλάντωση

  Ενέργειες και επιτάχυνση  στην φθίνουσα ταλάντωση

Η ταλάντωση πριν και μετά την πλαστική κρούση

      

Ένα σώμα Σ₁, μάζας m  εκτελεί ΑΑΤ, σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k, με πλάτος ταλάντωσης Α₀. Κάποια στιγμή αφήνεται από ορισμένο ύψος ένα δεύτερο σώμα Σ₂, μάζας Μ να πέσει, οπότε συγκρούεται πλαστικά με το σώμα Σ₁ και το συσσωμάτωμα ξεκινά μια νέα ΑΑΤ, με πλάτος ταλάντωσης Α₁.

i)  Να γίνει η γραφική παράσταση Α₁²=f(υ₁²), όπου υ₁ η ταχύτητα του Σ₁, ελάχιστα πριν την κρούση.

ii) Αν Μ=3m, να υπολογιστεί το ελάχιστο πλάτος ταλάντωσης του συσσωματώματος.

iii) Αν το ποσοστό απώλειας της κινητικής ενέργειας του συστήματος κατά την παραπάνω πλαστική κρούση, που οδηγεί σε ελάχιστο πλάτος, είναι ίσο με  87,5%, να υπολογιστεί ο λόγος U_2,αρχ/Ε_τ,1, όπου U_2,αρχ η αρχική δυναμική ενέργεια του Σ₂ τη στιγμή που αφήνεται να πέσει και Ε_τ,1 η αρχική ενέργεια ταλάντωσης του σώματος Σ₁.

Απάντηση:

ή

 Η ταλάντωση πριν και μετά την πλαστική κρούση

 Η ταλάντωση πριν και μετά την πλαστική κρούση

Η ενέργεια κατά την πλαστική κρούση, σε μια αατ

  

Ένα σώμα Α, μάζας m₁=2kg εκτελεί ΑΑΤ, σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου, με εξίσωση:

x=0,4∙ημ(10t) (μονάδες στο S.Ι.).

Ένα δεύτερο σώμα Β μάζας m₂=3kg κινείται κατά μήκος του άξονα του ελατηρίου, πλησιάζοντας το σώμα Α, με ταχύτητα μέτρου υ₂=1m/s.

i) Να υπολογιστεί η κινητική ενέργεια του συστήματος Κ_ολ των δύο σωμάτων σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση (Κ_ολ=f(t)).

ii) Τη στιγμή που η παραπάνω κινητική ενέργεια γίνεται ελάχιστη για δεύτερη φορά, τα δυο σώματα συγκρούονται πλαστικά.

α) Να βρεθεί το ποσοστό της κινητικής ενέργειας του συστήματος που μετατρέπεται σε θερμική ενέργεια λόγω της κρούσης.

β) Να υπολογιστεί ο λόγος Ε₂/Ε₁ όπου Ε₂ η ενέργεια ταλάντωσης του συσσωματώματος και Ε₁ η αντίστοιχη ενέργεια ταλάντωσης πριν την κρούση.

iii) Σε μια επανάληψη του ίδιου πειράματος το ποσοστό του ερωτήματος α) παίρνει τιμή 100%. Να υπολογιστεί η ενέργεια ταλάντωσης Ε₃ του συστήματος μετά την κρούση.

Απάντηση:

ή

 Η ενέργεια κατά την πλαστική κρούση, σε μια αατ

 Η ενέργεια κατά την πλαστική κρούση, σε μια αατ

Εμείς ασχολούμαστε με τον δίσκο!

 

  

Ένας δίσκος ηρεμεί στη θέση Ο, στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=100Ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος, όπως στο σχήμα, έχοντας συσπειρώσει το ελατήριο κατά 0,1m. Μια στιγμή (την οποία θεωρούμε ως t=0) αφήνουμε, χωρίς ταχύτητα, ένα σώμα Σ μάζας Μ=3kg, πάνω στο δίσκο, με αποτέλεσμα το σύστημα να ταλαντωθεί κατακόρυφα, ενώ στη θέση Β που μηδενίζεται για πρώτη φορά η ταχύτητα, αφαιρούμε το σώμα Σ, με αποτέλεσμα να ακολουθήσει μια νέα ταλάντωση του δίσκου.

i) Να υπολογιστούν τα πλάτη των δύο παραπάνω ταλαντώσεων.

ii) Να βρεθεί η συνάρτηση y=f(t) της θέσης του δίσκου, σε συνάρτηση με το χρόνο, όπου y=0 η αρχική θέση ισορροπίας του Ο και θετική η προς τα πάνω κατεύθυνση.

iii) Να παρασταθεί γραφικά παραπάνω συνάρτηση y=f(t), μέχρι τη στιγμή που ο δίσκος να επιστρέψει στην αρχική του θέση Ο (για πρώτη φορά).

iv) Για το ίδιο χρονικό διάστημα να παρασταθεί γραφικά η δύναμη του ελατηρίου η οποία ασκείται στο δίσκο, σε συνάρτηση με το χρόνο.

Δίνεται g=10m/s².

Απάντηση:

ή

 Εμείς ασχολούμαστε με τον δίσκο!

 Εμείς ασχολούμαστε με τον δίσκο!

Κάποια μέγιστα και ελάχιστα μετά από κρούση

  

Ένα σώμα Σ μάζας m₁=3kg εκτελεί ΑΑΤ, δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου, σε λείο οριζόντιο επίπεδο με εξίσωση:

x=0,2∙ημ(10t)  (S.Ι.)

Ένα δεύτερο σώμα Β, μάζας m₂=1kg κινείται κατά μήκος του άξονα του ελατηρίου με ταχύτητα υ₂=4m/s, πλησιάζοντας το Σ, με το οποίο κάποια στιγμή συγκρούεται κεντρικά και ελαστικά.

i)  Να υπολογιστεί η ενέργεια ταλάντωσης του σώματος Σ, πριν την κρούση.

ii) Αν η κρούση πραγματοποιείται τη στιγμή που το Σ περνά από την θέση ισορροπίας του, να υπολογιστεί η ενέργεια ταλάντωσής του μετά την κρούση.

iii) Μήπως αν η κρούση γίνει σε θέση πλάτους, έχουμε μεγαλύτερη ενέργεια ταλάντωσης, μετά την κρούση;

iv) Να βρεθεί η μέγιστη δυνατή ενέργεια ταλάντωσης του σώματος Σ, μετά την κρούση. Ποια  η ταχύτητα του σώματος Σ, ελάχιστα πριν και αμέσως μετά την παραπάνω κρούση;

Απάντηση:

ή

 Κάποια μέγιστα και ελάχιστα μετά από κρούση

 Κάποια μέγιστα και ελάχιστα μετά από κρούση