Δύο παράλληλοι αγωγοί

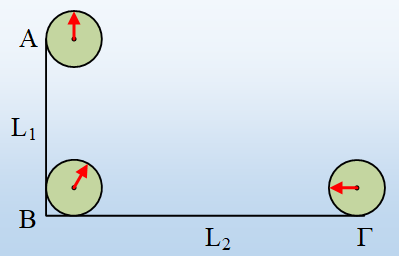
 Έστω ένα οριζόντιο τετράγωνο ΑΓΔΕ πλευράς α και δύο κατακόρυφοι αγωγοί, οι οποίοι διαρρέονται από ίσα ρεύματα, ο πρώτος να περνά από το κέντρο του τετραγώνου και ο δεύτερος από την κορυφή Γ. Η ένταση του μαγνητικού πεδίου στο μέσο Μ της πλευράς ΓΔ, η οποία οφείλεται στον πρώτο αγωγό, έχει μέτρο Β₁=0,4Τ.

i)  Να σχεδιάστε τα διανύσματα της έντασης του μαγνητικού πεδίου που δημιουργεί κάθε αγωγός στο σημείο Μ.

ii) Να υπολογίσετε την ένταση του πεδίου στο Μ που οφείλεται στον δεύτερο αγωγό.

iii) Να βρείτε την συνολική ένταση του πεδίου στο σημείο Μ. 

iv) Πόση δύναμη δέχεται ένα τμήμα μήκους 0,5m του δεύτερου αγωγού, με μέσο το σημείο Γ, αν μεταβάλουμε την ένταση του ρεύματος που τον διαρρέει στην τιμή Ι₂=10Α;

Απάντηση:

ή

  Δύο παράλληλοι αγωγοί

  Δύο παράλληλοι αγωγοί

Ασκήσεις Κρούσεων.

  

Παρακάτω θα βρείτε ένα αρχείο pdf, με όλες τις ασκήσεις πάνω στις κρούσεις, που έχω δημοσιεύσει στο ylikonet, αλλά και πριν από αυτό, στο  Blogspot.

Πρόκειται για 111 ασκήσεις- ερωτήσεις … μέχρι τις φετινές εξετάσεις.

Ασκήσεις κρούσεων

ή

 Ασκήσεις κρούσεων

ΥΣ

Ας σημειωθεί ότι δεν θα αναρτηθούν οι λύσεις των ασκήσεων, αφού αυτές έχουν αναρτηθεί σε καθεμία χωριστά τη στιγμή της δημοσίευσης. Αν κάποιος επιθυμεί λύση μιας συγκεκριμένης άσκησης, δεν έχει παρά να την αναζητήσει στο δίκτυό μας.

Θα μεταβληθεί η ένδειξη του αμπερομέτρου;

 Στο διπλανό σχήμα, ένας οριζόντιος κυκλικός αγωγός, συνδέεται σε ένα κύκλωμα, που περιλαμβάνει πηγή και ένα αμπερόμετρο, το οποίο δείχνει μια ορισμένη ένδειξη Ι_ο. Αφήνουμε από κάποιο ύψος έναν ραβδόμορφο μαγνήτη να πέσει με τον  Βόρειο πόλο του να πλησιάζει το κέντρο του κυκλικού αγωγού.

i) Τη στιγμή που ο μαγνήτης βρίσκεται στη θέση που δείχνει το σχήμα, η ένδειξη του αμπερομέτρου είναι Ι, όπου:

α) Ι < Ι_ο,   β)  Ι = Ι_ο,   γ) Ι > Ι_ο.

ii) Ποια θα ήταν η αντίστοιχη απάντηση στο παραπάνω ερώτημα, αν ο μαγνήτης έπεφτε με τον Νότιο πόλο του να πλησιάζει τον κυκλικό αγωγό;

Απάντηση:

ή

 Θα μεταβληθεί η ένδειξη του αμπερομέτρου;

 Θα μεταβληθεί η ένδειξη του αμπερομέτρου;

Ασκήσεις Ηλεκτρομαγνητισμού

Δίνω σε ένα αρχείο pdf όλες τις ασκήσεις πάνω στον Ηλεκτρομαγνητισμό, που έχω δημοσιεύσει στο ylikonet, αλλά και πριν από αυτό, στο  Blogspot.

Έτσι για να υπάρχουν και αυτές…

Ηλεκτρομαγνητισμός

ή

 Ηλεκτρομαγνητισμός

ΥΣ

Ας σημειωθεί ότι δεν θα αναρτηθούν οι λύσεις των ασκήσεων, αφού αυτές έχουν αναρτηθεί σε καθεμία χωριστά τη στιγμή της δημοσίευσης. Αν κάποιος επιθυμεί λύση μιας συγκεκριμένης άσκησης, δεν έχει παρά να την αναζητήσει στο δίκτυό μας.

Ασκήσεις Ταλαντώσεων

Δίνω σε ένα αρχείο pdf όλες τις ασκήσεις πάνω στις Ταλαντώσεις που έχω δημοσιεύσει στο ylikonet, αλλά και πριν από αυτό, στο  Blogspot.

Έτσι για να υπάρχουν…

Ταλαντώσεις

ή

 Ταλαντώσεις 

ΥΓ

Ας σημειωθεί ότι δεν θα αναρτηθούν οι λύσεις των ασκήσεων, αφού αυτές έχουν αναρτηθεί σε καθεμία χωριστά τη στιγμή της δημοσίευσης. Αν κάποιος επιθυμεί λύση μιας συγκεκριμένης άσκησης, δεν έχει παρά να την αναζητήσει στο δίκτυό μας.

Μηχανική Στερεού.

Παρακάτω θα βρείτε ένα αρχείο pdf, με όλες τις ασκήσεις πάνω στην Μηχανική στερεού, που έχω δημοσιεύσει στο ylikonet, αλλά και πριν από αυτό, στο  Blogspot. 

Πρόκειται για 482 ασκήσεις- ερωτήσεις ... μέχρι τις φετινές εξετάσεις.

Μηχανική Στερεού

ή

 Μηχανική Στερεού

ΥΣ

Ας σημειωθεί ότι δεν θα αναρτηθούν οι λύσεις των ασκήσεων, αφού αυτές έχουν αναρτηθεί σε καθεμία χωριστά τη στιγμή της δημοσίευσης. Αν κάποιος επιθυμεί λύση μιας συγκεκριμένης άσκησης, δεν έχει παρά να την αναζητήσει στο δίκτυό μας.

Ο μισός κυκλικό αγωγός σε μαγνητικό πεδίο.

 

Σε λείο οριζόντιο επίπεδο, ηρεμεί ένας οριζόντιος κυκλικός αγωγός ακτίνας R, κατά το ήμισυ μέσα σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β, όπως στο σχήμα.

Α) Μόλις κλείσουμε τον διακόπτη δ, ο αγωγός:

i) Θα μπει στο πεδίο,

ii) Θα βγει από το πεδίο,

iii) Το κέντρο του  Κ θα κινηθεί προς το σημείο Α παράλληλα προς το όριο του πεδίου,

iv) Το κέντρο του Κ θα κινηθεί παράλληλα προς το όριο του πεδίου, προς το σημείο Δ.

Β) Να αποδειχθεί ότι το μέτρο της δύναμης Laplace που θα ασκηθεί στον κυκλικό αγωγό, αμέσως μετά το κλείσιμο του διακόπτη, δίνεται από την εξίσωση F=2ΒΙR, όπου Ι η ένταση του ρεύματος που διαρρέει τον αγωγό.

Οι αγωγοί σύνδεσης του κυκλικού αγωγού με την πηγή, θεωρούνται ευλύγιστα λεπτά καλώδια, τα οποία επιτρέπουν την κίνηση του κυκλικού αγωγού.

Απάντηση:

ή

 Ο μισός κυκλικό αγωγός  σε μαγνητικό πεδίο.

 Ο μισός κυκλικό αγωγός  σε μαγνητικό πεδίο.

Μια ράβδος και η κινητική της ενέργεια.

 

Σε λείο οριζόντιο επίπεδο ηρεμεί μια ομογενής ράβδος ΑΒ μάζας m=6kg και μήκους ℓ=4m. Σε μια στιγμή t=0 ασκείται πάνω της μια σταθερή οριζόντια δύναμη, μέτρου F=3Ν, με αποτέλεσμα τη στιγμή t₁=2,14s η ράβδος να έχει περιστραφεί κατά 90°, όπως φαίνεται στο σχήμα (σε κάτοψη). Για τη στιγμή t₁ ζητούνται:

i) Η κινητική ενέργεια της ράβδου.

ii) Η ταχύτητα του άκρου Α της ράβδου.

iii) Ο ρυθμός μεταβολής της κινητικής ενέργειας της ράβδου.

Δίνεται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα ο οποίος περνά από το μέσον της Ι=mℓ²/12.

Απάντηση:

ή

 Μια ράβδος και η κινητική της ενέργεια.

 Μια ράβδος και η κινητική της ενέργεια.

Όταν το κιβώτιο μετατρέπεται σε σφαίρα

 

Ο κατακόρυφος οδηγός του σχήματος έχει σχήμα κοίλου τεταρτοκύκλιου ακτίνας R=1,4 m και είναι λείος και ακλόνητος. Ομογενής σφαίρα μάζας m και ακτίνας R=0,15m αφήνεται να ολισθήσει χωρίς τριβές από το άνω άκρο Α και φτάνει στο κάτω άκρο Β, οπότε και εγκαταλείπει τον οδηγό με οριζόντια ταχύτητα υ_Β.

Να βρεθούν :

i)  ο λόγος της γωνιακής ταχύτητας περιστροφής της σφαίρας προς την γωνιακή ταχύτητα περιφοράς της, σε κάθε σημείο της τροχιάς της.

ii)  όταν φτάσει στη θέση Β, ο λόγος της κινητικής μεταφορικής ενέργειας της σφαίρας προς την συνολική κινητική της ενέργεια.

iii) Η ταχύτητα της σφαίρας στο Β.

 Δίνεται g=10m/s².

Απάντηση:

ή

Όταν το κιβώτιο μετατρέπεται σε σφαίρα

 Όταν το κιβώτιο μετατρέπεται σε σφαίρα

Η περιφορά και η περιστροφή ενός δίσκου

 

Στο σχήμα βλέπετε μια αβαρή ράβδο ΓΔ μήκους l=2m, στα άκρα της οποίας έχουν συνδεθεί δύο ομογενείς δίσκοι Α και Β με ακτίνες r=0,5m. Ο δίσκος Α μπορεί να στρέφεται χωρίς τριβές γύρω από άρθρωση στο άκρο Γ της ράβδου, ενώ αντίθετα ο δίσκος Β έχει καρφωθεί, με το κέντρο του να ταυτίζεται με το δεξιό άκρο Δ, χωρίς δυνατότητα περιστροφής, παρά μόνο μαζί με την ράβδο. Ο Α έχει μάζα Μ=12,25kg και στρέφεται ωρολογιακά με γωνιακή ταχύτητα ω₀=4rad/s, ο Β έχει μάζα m=8kg, ενώ η ράβδος συγκρατείται σε οριζόντια θέση. Σε μια στιγμή t₀=0 αφήνουμε το σύστημα να κινηθεί, οπότε η ράβδος ΓΔ στρέφεται, χωρίς τριβές, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το μέσον της Κ. 

i)  Να υπολογιστεί η κινητική ενέργεια  του  δίσκου Β τη χρονική στιγμή t₁=1,3s, όπου η ράβδος γίνεται κατακόρυφη, για πρώτη φορά.

ii) Πόσες περιστροφές έχει εκτελέσει κάθε δίσκος, μέχρι τη στιγμή t₁;

iii) Ποιες οι αντίστοιχες απαντήσεις αν αρχικά ο δίσκος Α ηρεμούσε;

Δίνεται η ροπή αδράνειας ενός δίσκου ως προς κάθετο άξονα ο οποίος διέρχεται από το κέντρο του Ι_cm= ½ mR² και g=10m/s².

Απάντηση:

ή

 Η περιφορά και η περιστροφή ενός δίσκου

 Η περιφορά και η περιστροφή ενός δίσκου

Από την ευθύγραμμη τροχιά στην τεθλασμένη

  

Και από εκεί ξανά στο τεταρτοκύκλιο!!!

2) Ο παραπάνω δρόμος «σπάει» σε δύο άλλους ευθύγραμμους που σχηματίζουν ορθή γωνία, με μήκη L₁+L₂=L=14πr, όπου το τμήμα ΑΒ είναι κατακόρυφο και το ΒΓ οριζόντιο. Ένας δίσκος ξεκινά από το άκρο Α και φτάνει στο άκρο Γ, ενώ σε όλη τη διάρκεια της κίνησής του κυλίεται (προφανώς η μετακίνηση αυτή γίνεται προγραμματισμένα, περιστρέφοντας εμείς το δίσκο και όχι αφήνοντάς τον ελεύθερο να κινηθεί…).

Ο δίσκος θα πραγματοποιήσει 7 περιστροφές ή όχι και γιατί;

Απάντηση:

ή

 Από την ευθύγραμμη τροχιά στην τεθλασμένη

 Από την ευθύγραμμη τροχιά στην τεθλασμένη