Δυο ΑΑΤ και μια πλαστική κρούση

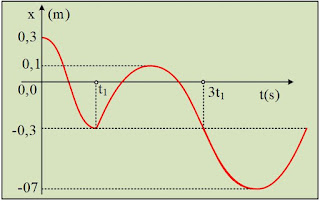
 Ένα σώμα Α μάζας m₁=1kg εκτελεί ΑΑΤ, δεμένο στο άκρο ιδανικού ελατηρίου. Τη στιγμή t₁ το σώμα Α συγκρούεται πλαστικά με ένα δεύτερο σώμα Β, το οποίο κινείται κατά μήκος του άξονα του ελατηρίου. Στο διάγραμμα βλέπετε την γραφική παράσταση της θέσης του σώματος Α (και του συσσωματώματος μετά την στιγμή t₁…) σε συνάρτηση με το χρόνο.

i)  Ποιο από τα παρακάτω σχήματα δείχνει τις θέσεις των σωμάτων λίγο πριν την κρούση;

 

Να δικαιολογήσετε την απάντησή σας.

ii) Με δεδομένο ότι το σχήμα που επιλέξατε περιγράφει την κατάσταση που μελετάμε και αντλώντας πληροφορίες από το παραπάνω  διάγραμμα, να βρείτε:

α) Την μάζα του Β σώματος.

β)  Την σταθερά k του ελατηρίου.

γ)  Την ταχύτητα του σώματος Β ελάχιστα πριν την κρούση.

Δίνεται g=10m/s².

Απάντηση:

ή

 Δυο ΑΑΤ και μια πλαστική κρούση

 Δυο ΑΑΤ και μια πλαστική κρούση

Μπορούμε να βρούμε από την ΑΑΤ, στοιχεία για την κρούση;

Ένα σώμα Α μάζας m₁ εκτελεί ΑΑΤ δεμένο στο άκρο οριζόντιου ιδανικού ελατηρίου, σε λείο οριζόντιο επίπεδο, όταν τη στιγμή t₁=1s συγκρούεται μετωπικά με ένα  δεύτερο σώμα Β. Στο διάγραμμα δίνεται η γραφική παράσταση της ταχύτητας του σώματος Α σε συνάρτηση με το χρόνο.

i)  Μπορείτε να εξηγήσετε γιατί η κρούση μεταξύ των δύο σωμάτων δεν μπορεί να είναι πλαστική;

ii) Ποιο από τα παρακάτω σχήματα δείχνει την εικόνα των δύο σωμάτων, ελάχιστα πριν την κρούση, αν η προς τα δεξιά κατεύθυνση θεωρηθεί ως θετική;

Δίνεται ότι η κρούση μεταξύ των σωμάτων είναι κεντρική και ελαστική, ενώ για τις μάζες ισχύει m₁=2m₂.

iii) Για το μέτρο της ταχύτητας του Β σώματος, πριν την κρούση, ισχύει:

α) |υ₂| < 3m/s,     β)  3m/s ≤ |υ₂| ≤ 5m/s,     γ) |υ₂| > 5m/s.

iv) Να υπολογιστεί η απόσταση των δύο σωμάτων τη χρονική στιγμή t₂=1,5s.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Μπορούμε να βρούμε από την ΑΑΤ στοιχεία για την κρούση;

 Μπορούμε να βρούμε από την ΑΑΤ στοιχεία για την κρούση;

Κάποιες γραφικές παραστάσεις στην ΑΑΤ.

  

Ένα σώμα μάζας 1kg ηρεμεί  στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=100Ν/m. Μετακινούμε το σώμα κατακόρυφα προς τα πάνω, μέχρι την θέση Β όπου το ελατήριο έχει συσπειρωθεί κατά Δℓ =0,1m και κάποια στιγμή που θεωρούμε ως αρχή μέτρησης των χρόνων (t=0), το αφήνουμε να ταλαντωθεί, εκτελώντας ΑΑΤ, με μηδενική αρχική ταχύτητα.

i) Να βρεθεί το πλάτος και η περίοδος ταλάντωσης.

ii) Θεωρώντας την προς τα πάνω κατεύθυνση ως θετική, να βρεθούν οι εξισώσεις και να γίνουν οι γραφικές παραστάσεις σε συνάρτηση με το χρόνο:

α) της απομάκρυνσης του σώματος, από την θέση ισορροπίας.

β) της ταχύτητας του σώματος

γ) της δύναμης επαναφοράς.

δ) της δύναμης του ελατηρίου.

iii) Να γίνουν οι γραφικές παραστάσεις της δυναμικής ενέργειας ταλάντωσης σε συνάρτηση:

α) με την απομάκρυνση του σώματος.

β) με τον χρόνο.

Δίνεται g=10m/s².

Απάντηση:

ή

 Κάποιες γραφικές παραστάσεις στην ΑΑΤ.

 Κάποιες γραφικές παραστάσεις στην ΑΑΤ.

Μια ελαστική κρούση και το διάγραμμα θέσης

  

Δύο σώματα Α και Β ηρεμούν σε οριζόντιο απέχοντας μεταξύ τους απόσταση d, ελεύθερα να κινηθούν. Σε μια στιγμή t₀=0 το σώμα Α, μάζας m₁=1kg, δέχεται ένα στιγμιαίο κτύπημα, αποκτώντας κάποια ταχύτητα, με κατεύθυνση προς το σώμα Β, με το οποίο συγκρούεται κεντρικά και ελαστικά τη στιγμή t₁. Θεωρώντας την αρχική θέση του σώματος Α, ως αρχή ενός προσανατολισμένου άξονα x και θεωρώντας αμελητέα τη διάρκεια της κρούσης, παίρνουμε το διπλανό διάγραμμα της θέσης x, σε συνάρτηση με το χρόνο.

i)  Το οριζόντιο επίπεδο είναι λείο ή όχι;

ii) Αν m₂ η μάζα του Β σώματος, ισχύει:

α) m₁ < m₂,     β) m₁ = m₂,    γ) m₁ > m₂,

iii) Για τις χρονικές στιγμές t₁ και t₂ ισχύει:

α) t₂ < 2t₁,      β) t₂ = 2t₁,     γ) t₂ > 2t₁.

iv) Επαναλαμβάνουμε το πείραμα, παίρνοντας τώρα ακριβείς μετρήσεις, οπότε σχεδιάζοντας το διάγραμμα  x-t, παίρνουμε το διπλανό διάγραμμα. Να υπολογιστούν η ορμή και η κινητική ενέργεια του Β σώματος, αμέσως μετά την κρούση.

Απάντηση:

ή

 Μια ελαστική κρούση και το διάγραμμα θέσης

 Μια ελαστική κρούση και το διάγραμμα θέσης

 Μια ελαστική κρούση και το διάγραμμα θέσης

Όταν ακόμη και ο τοίχος …υποχωρεί!

  

Μια σφαίρα μάζας m₁=1kg κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα μέτρου υ₁=5m/s (χωρίς να στρέφεται) και συγκρούεται ελαστικά με έναν πακτωμένο ακλόνητο κύβο μάζας m₂=2kg. Το σημείο κρούσης είναι το κέντρο μιας έδρας του κύβου, ενώ η ταχύτητα υ₁ σχηματίζει με την κάθετη στην έδρα στο σημείο κρούσης, γωνία θ, όπου ημθ=0,8 και συνθ=0,6, όπως φαίνεται στο σχήμα (σε κάτοψη). Αν δεν αναπτύσσεται τριβή μεταξύ των συγκρουόμενων σωμάτων και υ₁΄ η ταχύτητα της σφαίρας μετά την κρούση, να βρεθούν:

i) Η μεταβολή της κινητικής ενέργειας και η μεταβολή της ορμής:

α) της σφαίρας,   β) του κύβου και γ) του συστήματος των δύο σωμάτων

 που οφείλονται στην κρούση.

ii) Επαναλαμβάνουμε το ίδιο πείραμα, με μόνη διαφορά, ότι έχουμε αφαιρέσει την πάκτωση και ο κύβος έχει την δυνατότητα να κινηθεί, μετά την κρούση. Ποιες θα είναι τώρα οι αντίστοιχες απαντήσεις στα παραπάνω ερωτήματα;

Απάντηση:

ή

  Όταν ακόμη και ο τοίχος …υποχωρεί!

  Όταν ακόμη και ο τοίχος …υποχωρεί!

Πληροφορίες για μια κρούση από ένα διάγραμμα

  

Δύο σώματα Α και Β με μάζες m₁=2kg και m₂=3kg αντίστοιχα, ηρεμούν σε οριζόντιο επίπεδο με το οποίο εμφανίζουν τον ίδιο συντελεστή τριβής ολίσθησης μ, απέχοντας μεταξύ τους απόσταση d₁. Σε μια στιγμή t₀=0 το σώμα Α, δέχεται ένα στιγμιαίο κτύπημα, αποκτώντας αρχική ταχύτητα υ₀=7m/s, με κατεύθυνση προς το σώμα Β. Μετά από λίγο τα δυο σώματα συγκρούονται μετωπικά και στο διάγραμμα δίνεται η ταχύτητα του σώματος Β σε συνάρτηση με το χρόνο.

i)  Να βρεθεί ο συντελεστής τριβής ολίσθησης μ μεταξύ του επιπέδου και των δύο σωμάτων.

ii) Να υπολογιστεί η αρχική απόσταση d₁ μεταξύ των δύο σωμάτων.

iii) Να βρεθεί η ταχύτητα του Α σώματος αμέσως μετά την κρούση.

iv) Η παραπάνω κρούση μεταξύ των σωμάτων, είναι ή όχι ελαστική;

v) Να βρεθεί η τελική απόσταση d₂ μεταξύ των δύο σωμάτων, όταν πάψουν να κινούνται.

Δίνεται g=10m/s².

Απάντηση:

ή

  Πληροφορίες για μια κρούση από ένα διάγραμμα

  Πληροφορίες για μια κρούση από ένα διάγραμμα

  Πληροφορίες για μια κρούση από ένα διάγραμμα

Ένα μηχανικό σύστημα σε οριζόντια κίνηση

  

Σε λείο οριζόντιο επίπεδο ηρεμούν δύο σφαίρες Α και Β με μάζες m₁=1kg και m₂=4kg, δεμένες στα άκρα ιδανικού ελατηρίου σταθεράς k=75Ν/m, ο άξονας του οποίου ταυτίζεται με τον άξονα x, ενός ορθογωνίου συστήματος οριζοντίων αξόνων x,y. Σε μια στιγμή η σφαίρα Α δέχεται στιγμιαίο κτύπημα, με αποτέλεσμα να αποκτά οριζόντια ταχύτητα κάθετη στον άξονα του ελατηρίου (στην διεύθυνση y) μέτρου υ₀=4m/s. Μετά από λίγο, τη στιγμή t₁, η Α σφαίρα έχει ταχύτητα στην διεύθυνση x, μέτρου υ₁=3m/s, όπως στο σχήμα. Για την στιγμή αυτή:

i)   Να υπολογιστούν οι συνιστώσες ταχύτητας της Β σφαίρας στους άξονες x και y και στη συνέχεια να βρεθεί και η ταχύτητα της σφαίρας υ₂.

ii) Να υπολογιστεί η απώλεια της κινητικής ενέργειας του συστήματος των δύο σφαιρών.

iii) Να βρεθεί το μέτρο του ρυθμού μεταβολής της ορμής της σφαίρας Α.

iv) Μια επόμενη στιγμή t₂, το μέτρο της ταχύτητας της Α σφαίρας είναι υ_Α=4m/s.  Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής της Β σφαίρας, τη στιγμή αυτή;

Απάντηση:

ή

 Ένα μηχανικό σύστημα σε οριζόντια κίνηση

 Ένα μηχανικό σύστημα σε οριζόντια κίνηση

 Ένα μηχανικό σύστημα σε οριζόντια κίνηση

Πληροφορίες από ένα διάγραμμα ορμής.

  

Στο διπλανό διάγραμμα δίνεται η μεταβολή της ορμής του σώματος Α, μάζας m₁=m, που οφείλεται στην κεντρική ελαστική κρούση του με ένα δεύτερο σώμα Β, μάζας m₂=2m. Τα σώματα βρίσκονται σε λείο οριζόντιο επίπεδο και η προς τα δεξιά κατεύθυνση θεωρείται θετική.

i) Το σώμα Β πριν την κρούση:

α) Είναι ακίνητο.

β) Κινείται προς τα δεξιά.

γ) Κινείται προς τα αριστερά.

ii) «Τη χρονική στιγμή t₁ που μηδενίζεται η ορμή του Α σώματος, τα δυο σώματα έχουν τις ελάχιστες κινητικές τους ενέργειες». Συμφωνείτε ή διαφωνείτε με την πρόταση αυτή;

iii) Η τελική ορμή του σώματος Β είναι ίση:

α) α,   β)  2,5 α,    γ) 4,5 α,    δ) 5,5 α.

Απάντηση.

ή

  Πληροφορίες από ένα διάγραμμα ορμής.

  Πληροφορίες από ένα διάγραμμα ορμής.

 Πληροφορίες από ένα διάγραμμα ορμής.

Δύο σφαίρες συγκρούονται σε οριζόντιο επίπεδο

Μια σφαίρα Α κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ₁ και συγκρούεται με μια δεύτερη σφαίρα Β, ίσης ακτίνας αλλά διαφορετικής μάζας, η οποία ηρεμούσε. Θεωρούμε το ορθογώνιο σύστημα αξόνων με αρχή Ο την αρχική θέση της Β σφαίρας, ενώ ο άξονας x΄x συμπίπτει με την διεύθυνση της αρχικής ταχύτητας της Α σφαίρας όπως στο σχήμα (σε κάτοψη). Μετά την κρούση η Α σφαίρα κινείται κατά μήκος του ημιάξονα Οy.

Η σφαίρα Β θα κινηθεί:

i) Κατά μήκος του ημιάξονα Οx.

ii) Κατά μήκος του ημιάξονα Οy΄.

iii) Πάνω στη διχοτόμο της ορθής γωνία y΄Ο x.

iv) Τίποτα από τα παραπάνω.

Να δικαιολογήσετε την επιλογή σας.

Απάντηση:

ή

 Δύο σφαίρες συγκρούονται σε οριζόντιο επίπεδο

 Δύο σφαίρες συγκρούονται σε οριζόντιο επίπεδο

  Δύο σφαίρες συγκρούονται σε οριζόντιο επίπεδο

Μια κεντρική κρούση δύο σφαιρών

  

Δύο σφαίρες με ίσες ακτίνες κινούνται σε λείο οριζόντιο επίπεδο, χωρίς να στρέφονται. Στο διάγραμμα δίνεται η ταχύτητα της Α σφαίρας μάζας m₁=1kg, όπου τη στιγμή t₁ έχουμε μια κεντρική κρούση μεταξύ των δύο σφαιρών.

i)  Να υπολογιστεί η μεταβολή της ορμής κάθε σφαίρας, που οφείλεται στην κρούση.

ii) Να παρασταθεί γραφικά η ορμή της Β σφαίρας σε συνάρτηση με το χρόνο, αν

α) πριν την κρούση έχει ταχύτητα προς τα δεξιά και ορμή μέτρου p₂=6kg∙m/s.

β) πριν την κρούση έχει ταχύτητα προς τα αριστερά και ορμή μέτρου p₂=2kg∙m/s.

iii) Να υπολογισθεί η αύξηση της κινητικής ενέργειας της σφαίρας Β, στην α) περίπτωση, αν η κρούση μεταξύ των σφαιρών είναι ελαστική.

iv) Να υπολογιστεί η μάζα της σφαίρας Β, αν έχουμε ελαστική κρούση και αρχικά η σφαίρα ήταν ακίνητη.

Απάντηση:

ή

 Μια κεντρική κρούση δύο σφαιρών 

 Μια κεντρική κρούση δύο σφαιρών 

 Μια κεντρική κρούση δύο σφαιρών

Η ισχύς με ανοικτό και κλειστό διακόπτη

  

Δίνεται το διπλανό κύκλωμα, με ανοικτό το διακόπτη δ, όπου R₁=6Ω, η τάση της πηγής είναι της μορφής υ=30√2∙ημ(20πt), ενώ το αμπερόμετρο δείχνει ένδειξη 3 Α.

i)  Να βρεθεί η αντίσταση R₂.

ii)  Να βρεθεί το χρονικό διάστημα μεταξύ δύο διαδοχικών μηδενισμών της έντασης του ρεύματος, καθώς και η στιγμιαία ισχύς του ρεύματος, τη χρονική στιγμή που η φάση της πηγής είναι ίση με φ=5π/4 rad.

iii) Να υπολογιστεί η μέση ισχύς του ρεύματος στην αντίσταση R₁, καθώς και ο μέγιστος ρυθμός με τον οποίο παράγεται θερμότητα πάνω στην R₁.

iv) Σε μια στιγμή κλείνουμε το διακόπτη δ. Πόσο τοις εκατό θα αυξηθεί η μέση ισχύς που καταναλώνει η αντίσταση R₁, με το κλείσιμο του διακόπτη;

Απάντηση:

ή

 Η ισχύς με ανοικτό και κλειστό διακόπτη

 Η ισχύς με ανοικτό και κλειστό διακόπτη

 Η ισχύς με ανοικτό και κλειστό διακόπτη

Ο χρόνος και η ταχύτητα πτώσης του αγωγού.

Στο διπλανό σχήμα ο αγωγός ΑΓ, μπορεί να κινείται σε επαφή με δύο κατακόρυφους αγωγούς, xx΄ και yy΄, χωρίς τριβές. Μια αντίσταση R συνδέεται μεταξύ x και y, ενώ παρεμβάλλεται ένας ανοικτός διακόπτης δ. Το όλο σύστημα βρίσκεται μέσα σε ένα οριζόντιο ομογενές μαγνητικό πεδίο με ένταση κάθετο στο επίπεδο της σελίδας με φορά προς τον αναγνώστη. Με το διακόπτη δ ανοικτό, αφήνουμε ελεύθερο τον αγωγό ΑΓ να κινηθεί από την θέση (1), οπότε μετά από χρόνο t₁, περνά από την θέση (2) με ταχύτητα υ₁.  

Επαναλαμβάνουμε το πείραμα, αφού προηγούμενα κλείσουμε το διακόπτη δ, οπότε αφήνοντας ξανά τον αγωγό να πέσει, αυτός περνά από την θέση (2) μετά από χρονικό διάστημα t₂, με ταχύτητα υ₂.

i) Για τα χρονικά διαστήματα t₁ και t₂ ισχύει:

α) t₁< t₂,    β) t₁ = t₂,    γ) t₁  > t₂.

ii) Για τα μέτρα των ταχυτήτων υ₁ και υ₂ ισχύει:

α) υ₁< υ₂,    β) υ₁ = υ₂,    γ) υ₁ > υ₂.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Ο χρόνος και η ταχύτητα πτώσης του αγωγού.

 Ο χρόνος και η ταχύτητα πτώσης του αγωγού.

 Ο χρόνος και η ταχύτητα πτώσης του αγωγού.

Μια ερμηνεία και ένας υπολογισμός

Ο αγωγός ΑΓ, κινείται σε οριζόντιο επίπεδο σε επαφή με δύο μεταλλικούς παράλληλους στύλους, μέσα σε ένα κατακόρυφο μαγνητικό πεδίο, όπως στο πάνω σχήμα, με την επίδραση μιας σταθερής εξωτερική δύναμης μέτρου F_εξ=3Ν. Παίρνοντας κάποια θέση ως αρχή μέτρησης των μετατοπίσεων, κατασκευάσαμε το διάγραμμα, όπως στο κάτω σχήμα της ταχύτητα του ΑΓ σε συνάρτηση με την μετατόπισή του.

Δίνεται ότι ο αγωγός έχει μάζα m=0,4kg και δεν εμφανίζονται τριβές στη διάρκεια της κίνησής του, ενώ η ασκούμενη εξωτερική δύναμη δεν μεταβάλλεται.

i)   Η μορφή της γραφικής παράστασης ερμηνεύεται με βάση τη συλλογιστική ότι στη διάρκεια της κίνησης, μέχρι και την θέση με x=1m, το μαγνητικό πεδίο είναι ομογενές, ενώ στη συνέχεια η έντασή του μειώνεται. Συμφωνείτε με την παραπάνω ερμηνεία; Αν ναι, τι δικαιολόγηση δίνετε, αν όχι ποια ερμηνεία δίνετε εσείς;

ii) Αν Q₁ η θερμότητα που εμφανίζεται στο κύκλωμα μέχρι τη θέση x₁=1m και Q₂ η αντίστοιχη θερμότητα στη συνέχεια μέχρι και την θέση x₂=2m, ισχύει:

α) Q₁=0,2Q₂,   β) Q₁=0,5Q₂,  γ) Q₁=2Q₂,    δ) Q₁=5Q₂.

Να δικαιολογήσετε την απάντησή σας.

Απάντηση:

ή

 Μια ερμηνεία και ένας υπολογισμός

 Μια ερμηνεία και ένας υπολογισμός

 Μια ερμηνεία και ένας υπολογισμός