Η αλγεβρική τιμή και το μέτρο της δύναμης

 

Η ομογενής δοκός ΑΒ μάζας Μ, μπορεί να στρέφεται γύρω από άρθρωση στο άκρο της Α και ισορροπεί οριζόντια, όταν στο άκρο της Β κρέμεται μέσω ελατηρίου ένα σώμα Σ, μάζας m, ενώ συγκρατείται μέσω νήματος, το οποίο έχουμε δέσει στο σημείο Ρ, όπως στο σχήμα. Κάποια στιγμή θέτουμε το Σ σε κατακόρυφη ταλάντωση με πλάτος Α=2mg/k.

i)   Θεωρώντας την προς τα πάνω κατεύθυνση ως θετική, η αλγεβρική τιμή της δύναμης του ελατηρίου η οποία ασκείται στο σώμα Σ, σε συνάρτηση της απομάκρυνσης y, δίνεται από την σχέση:

α) F_ελ=-mg+ky,    β) F_ελ=mg-ky,    γ)  F_ελ=-mg-ky

ii)  Αν κατά την παραπάνω ταλάντωση οριακά εξασφαλίζεται η ισορροπία της ράβδου, χωρίς να λυγίζει το νήμα, τότε για τις μάζες Μ και m ισχύει:

α) Μ=m,   β) Μ=2m,    γ) Μ=3m,   δ) Μ=4m.

Απάντηση:

ή

 Η αλγεβρική τιμή και το μέτρο της δύναμης

 Η αλγεβρική τιμή και το μέτρο της δύναμης

Δύο ασύμβατα κάθετοι αγωγοί.

 

Στο επίπεδο της σελίδας υπάρχει ένας ευθύγραμμος αγωγός, ο οποίος διαρρέεται από ηλεκτρικό ρεύμα έντασης Ι₁. Κάθετα στο επίπεδο της σελίδας, βρίσκεται ένας άλλος ευθύγραμμος αγωγός, ο οποίος διαρρέεται από ρεύμα έντασης Ι₂, με φορά προς τα μέσα, όπως στο σχήμα, στο σημείο Ο του επιπέδου. Η ΟΑ=d είναι η (κάθετη) απόσταση μεταξύ των δύο αγωγών, ενώ η ΟΓ σχηματίζει γωνία θ με την ΑΓ.

i)  Αν Β₁ το μέτρο της έντασης του μαγνητικού πεδίου του δεύτερου αγωγού στο σημείο Α και Β₂ η αντίστοιχη ένταση στο σημείο Γ, ισχύει:

α) Β₁/Β₂= 1,    β)  Β₁/Β₂= ημθ,   γ) Β₁/Β₂= συνθ,    δ) Β₁/Β₂= 1/ημθ.

ii)  Να χαρακτηρίσετε τις παρακάτω προτάσεις, οι οποίες αναφέρονται στις δυνάμεις που ασκούνται σε δυο στοιχειώδη μήκη dl του πρώτου αγωγού στις θέσεις Α και Γ, ως σωστές ή λανθασμένες δίνοντας σύντομες δικαιολογήσεις.

α)  Στο τμήμα dl στη θέση Α δεν ασκείται δύναμη Laplace από το μαγνητικό πεδίο του αγωγού στο Ο.

β)  Η δύναμη που δέχεται το τμήμα dl στη θέση Γ είναι κάθετη στη σελίδα, με φορά προς τα έξω.

γ)  Το μέτρο της δύναμης Laplace η οποία ασκείται στο τμήμα dl στη θέση Γ, είναι ανάλογο του ημίτονου της γωνίας θ.

Δίνεται ημ2θ=2ημθ∙συνθ

Απάντηση:

ή

 Δύο ασύμβατα κάθετοι αγωγοί.

 Δύο ασύμβατα κάθετοι αγωγοί.

Το έργο δύναμης σε κρούσεις

 

i)  Δύο σφαίρες Α και Β κινούνται προς την ίδια κατεύθυνση, σε λείο οριζόντιο επίπεδο και  σε μια στιγμή συγκρούονται κεντρικά και ελαστικά, οπότε μεταξύ τους ασκούνται οι δυνάμεις F₁ και F₂ στη διάρκεια της κρούσης. Για το έργο της δύναμης F₁ ισχύει:

α) W < 0 ,   β) W=0,    γ) W > 0

Διαβάστε τη συνέχεια…

 ή

 Το έργο δύναμης σε κρούσεις

 Το έργο δύναμης σε κρούσεις

Η μεταβολή της έντασης Μ.Π. σε ένα πλαίσιο

 

Ένα ορθογώνιο, βρίσκεται με το επίπεδό του κάθετο σε ένα μαγνητικό πεδίο, η ένταση του οποίου μεταβάλλεται, όπως στο διπλανό διάγραμμα.

Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες, δίνοντας σύντομες δικαιολογήσεις:

i)  Η μαγνητική ροή που διέρχεται από το πλαίσιο τη στιγμή t₂ είναι θετική και έχει μεγαλύτερη τιμή από την αντίστοιχη τιμή τη στιγμή t₁.

ii) Από 0 – t₂ το πλαίσιο διαρρέεται από ηλεκτρικό ρεύμα σταθερής έντασης, με φορά από το Α στο Δ.

iii) Στο παραπάνω χρονικό διάστημα στο πλαίσιο ασκείται δύναμη Laplace, με κατεύθυνση αντίθετη της έντασης του μαγνητικού πεδίου, αφού σύμφωνα με τον κανόνα του Lenz η δύναμη αντιστέκεται στην αύξηση του Β.

Απάντηση:

ή

 Η μεταβολή της έντασης Μ.Π.  σε ένα πλαίσιο

 Η μεταβολή της έντασης Μ.Π.  σε ένα πλαίσιο

Ανελαστική ή πλαστική κρούση δύο ράβδων

 

Σε λείο οριζόντιο επίπεδο ηρεμούν δύο όμοιες οριζόντιες ομογενείς ράβδοι μήκους l=4m και μάζας m=3kg η καθεμιά. Σε μια στιγμή εκτοξεύουμε την ράβδο ΑΒ με αρχική ταχύτητα υ₀=4m/s κάθετη προς την ράβδο ΓΔ, όπως στο σχήμα, οπότε τη στιγμή της κρούσης οι ράβδοι είναι κάθετες, ενώ συγκρούονται τα άκρα τους Β και Δ.

i)   Αν η ταχύτητα της πρώτης ράβδου ΑΒ μετά την κρούση έχει μέτρο υ₁=2,5m/s, με φορά προς τα δεξιά, η κρούση μεταξύ των δύο ράβδων είναι:

α) Ελαστική,    β) Ανελαστική,    γ) Πλαστική.

ii) Ποια θα ήταν η αντίστοιχη απάντησή σας αν η ταχύτητα της πρώτης ράβδου μετά την κρούση είχε μέτρο υ₁₁=3,2m/s.

Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που περνά από το μέσον της Ι_cm= ml²/12.

Απάντηση:

ή

Ανελαστική ή πλαστική κρούση δύο ράβδων

Ανελαστική ή πλαστική κρούση δύο ράβδων

Κίνηση σε ομογενές και μη ομογενές μαγνητικό πεδίο

1) Στο διπλανό σχήμα, ένα τετράγωνο αγώγιμο πλαίσιο ΑΓΔΖ κινείται οριζόντια σε λείο οριζόντιο επίπεδο, όταν συναντά μια περιοχή στην οποία υπάρχει ένα ομογενές κατακόρυφο μαγνητικό πεδίο. Η ταχύτητα του πλαισίου, μόλις ολοκληρώνεται η είσοδός του στο πεδίο είναι υ₁ και η ταχύτητά του τη στιγμή που ετοιμάζεται να βγει είναι υ₂.

Ποιες προτάσεις είναι σωστές και ποιες λανθασμένες:

i) Στην παραπάνω κίνηση, το πλαίσιο διαρρέεται από ηλεκτρικό ρεύμα λόγω επαγωγής.

ii) Η φορά του ρεύματος είναι από το Γ στο Α.

iii) Το πλαίσιο δέχεται  δύναμη από το πεδίο με φορά προς τα αριστερά.

iv) Για τα μέτρα των ταχυτήτων ισχύει υ₁=υ₂.

Να δικαιολογήσετε τις απαντήσεις σας.

 2) Στο διπλανό σχήμα, ένα τετράγωνο αγώγιμο πλαίσιο ΑΓΔΖ κινείται οριζόντια σε λείο οριζόντιο επίπεδο, όταν συναντά μια περιοχή στην οποία υπάρχει ένα κατακόρυφο μαγνητικό πεδίο, η ένταση του οποίου μειώνεται καθώς κινούμαστε προς τα δεξιά. Η ταχύτητα του πλαισίου, μόλις ολοκληρώνεται η είσοδός του στο πεδίο είναι υ₁ και η ταχύτητά του τη στιγμή που ετοιμάζεται να βγει είναι υ₂.

Ποιες προτάσεις είναι σωστές και ποιες λανθασμένες:

i)  Στην παραπάνω κίνηση, το πλαίσιο διαρρέεται από ηλεκτρικό ρεύμα λόγω επαγωγής.

ii) Η φορά του ρεύματος είναι από το Γ στο Α.

iii) Το πλαίσιο δέχεται  δύναμη από το πεδίο με φορά προς τα αριστερά.

iv) Για τα μέτρα των ταχυτήτων ισχύει υ₁=υ₂.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Κίνηση σε ομογενές και μη ομογενές μαγνητικό πεδίο

 Κίνηση σε ομογενές και μη ομογενές μαγνητικό πεδίο

Η στατική τριβή και η μέγιστη δύναμη.

Δύο σώματα ίσης μάζας Σ₁ και Σ₂ βρίσκονται εκατέρωθεν σώματος Σ₃ το οποίο παρουσιάζει με το δάπεδο τριβή, με συντελεστή με συντελεστή οριακής τριβής μ. Τα σώματα Σ₁ και Σ₂ δεν παρουσιάζουν τριβή με το δάπεδο και είναι δεμένα με το Σ₃ μέσω ελατηρίων σταθερών k₁ = k και k₂ = 4k, όπως φαίνεται στο σχήμα. Απομακρύνουμε τα σώματα Σ₁ και Σ₂ από τις θέσεις ισορροπίας τους ώστε και τα δύο ελατήρια να επιμηκυνθούν κατά Α. Την χρονική στιγμή t = 0, αφήνουμε ταυτόχρονα τα δύο σώματα να εκτελέσουν Α.Α.Τ.

Α. Η ελάχιστη τιμή της μάζας Μ του Σ₃ για να παραμένει ακίνητο κατά την διάρκεια της ταλάντωσης των άλλων δύο είναι:

α. M = 5kA/μg                          β. M = 3kA/μg                           γ. M = kA/μg

Β. Η χρονική στιγμή t₁ που το Σ₃ δέχεται για πρώτη φορά την μέγιστη δύναμη είναι:

α. t₁ = (π/2)√(m/k)                     β. t₁ = (π)√(m/k)                          γ. t₁ = (2π)√(m/k)
Η συνέχεια εδώ.

Οι ταχύτητες πριν και μετά την κρούση

 

Μια σφαίρα Σ₁ μάζας m κινείται σε λείο οριζόντιο επίπεδο, προς τα δεξιά, με ταχύτητα υ₁ και συγκρούεται κεντρικά και ελαστικά με δεύτερη κινούμενη σφαίρα Σ₂ ίσης ακτίνας, με αποτέλεσμα μετά την κρούση, να κινείται προς τα αριστερά με ταχύτητα υ₁΄ ίσου μέτρου (υ₁΄=υ₁).

i) Η σφαίρα Σ₂ πριν την κρούση:

α) Κινείται προς τα δεξιά.

β) κινείται προς τα αριστερά.

ii) Αν η σφαίρα Σ₂ έχει μάζα m₂=2m, τότε για το μέτρο της ταχύτητας υ₂΄ της δεύτερης σφαίρας, μετά την κρούση, ισχύει:

α) υ₂΄< υ₁/2,   β) υ₂΄=υ₁/2,   γ) υ₂΄> υ₁/2

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Οι ταχύτητες πριν και μετά την κρούση

Οι ταχύτητες πριν και μετά την κρούση

Όταν δεν έχουμε «μια στιγμούλα», αλλά δύο!

 

Μια ομογενής ράβδος ΑΒ συγκρατείται στη θέση (α), δεμένη στο μέσον της Μ με αβαρές νήμα ΜΟ (1^ο ενδεχόμενο) ή καρφωμένη (πακτωμένη) σταθερά με αβαρή ράβδο ΜΟ, η οποία μπορεί να στρέφεται γύρω από το άκρο της Ο (2^ο ενδεχόμενο). Σε μια στιγμή αφήνουμε ελεύθερη τη ράβδο και μετά από λίγο περνά από τη θέση (β), όπου γίνεται οριζόντια.

Να χαρακτηρισθούν ως σωστές ή λανθασμένες οι παρακάτω προτάσεις, δίνοντας τις κατάλληλες δικαιολογήσεις:

i) Η κίνηση της ράβδου δεν μπορεί να χαρακτηρισθεί ως μεταφορική.

ii) Αν η ράβδος είναι δεμένη με αβαρές νήμα ( 1^η περίπτωση), τότε υπεύθυνη για την περιστροφή της ράβδου γύρω από το Ο, είναι η ροπή του βάρους ως προς το σημείο πρόσδεσης Ο.

iii) Η ράβδος του σχήματος έχει προσδεθεί στο άκρο αβαρούς ράβδου ΟΜ (2^η περίπτωση) και όχι αβαρούς νήματος.

Απάντηση:

ή

 Όταν δεν έχουμε «μια στιγμούλα», αλλά δύο!

 Όταν δεν έχουμε «μια στιγμούλα», αλλά δύο!

Όταν δεν στρέφεται το πλαίσιο, αλλά…

Ο μαγνήτης

Ένα τετράγωνο μεταλλικό πλαίσιο πλευράς α=0,5m και με αντίσταση R=0,5Ω, βρίσκεται μέσα σε ένα ομογενές μαγνητικό πεδίο, κάθετα στις δυναμικές γραμμές, όπως στο διπλανό σχήμα (σε κάτοψη).

Να χαρακτηρίσετε τις παρακάτω προτάσεις στις ερωτήσεις i) και ii) ως σωστές ή λανθασμένες, δίνοντας σύντομες δικαιολογήσεις.

i) Αν η ένταση του μαγνητικού πεδίου, μεταβάλλεται όπως στο σχήμα (α), τότε:

α) Τη χρονική στιγμή t₁ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Α στο Β.

β) Τη χρονική στιγμή t₁ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Β στο Α.

γ) Τη χρονική στιγμή t₂ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Α στο Β.

δ) Τη χρονική στιγμή t₂ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Β στο Α.

ii) Αν η ένταση του μαγνητικού πεδίου, μεταβάλλεται αρμονικά όπως στο σχήμα (β), τότε:

α) Τη χρονική στιγμή t₁ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Α στο Β.

β) Τη χρονική στιγμή t₁ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Β στο Α.

γ) Τη χρονική στιγμή t₂ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Α στο Β.

δ) Τη χρονική στιγμή t₂ το πλαίσιο διαρρέεται από ρεύμα με φορά από το Β στο Α.

iii) Να υπολογιστεί η συνολική θερμότητα που θα παραχθεί πάνω στο πλαίσιο στις δυο παραπάνω περιπτώσεις από τη στιγμή μηδέν έως τη στιγμή 0,2s.

Απάντηση:

ή

Όταν δεν στρέφεται το πλαίσιο, αλλά…

Όταν δεν στρέφεται το πλαίσιο, αλλά…

Επαγωγή και δύο αγωγοί

Οι οριζόντιοι αγωγοί ΑΓ και ΔΖ, με ίσες αντιστάσεις R₁=R₂=R, μπορούν να κινούνται σε επαφή με δύο οριζόντιους στύλους, χωρίς αντίσταση, μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο. Ο αγωγός ΑΓ κινείται με ταχύτητα υ, ενώ ο ΔΖ είναι ακίνητος, όπως στο σχήμα. Σε μια στιγμή κλείνουμε το διακόπτη.
Ποιες προτάσεις είναι σωστές και ποιες λάθος. Να δικαιολογήσετε τις απαντήσεις σας.

i)  Στον αγωγό ΑΓ αναπτύσσεται ΗΕΔ από επαγωγή, ανάλογη της ταχύτητας υ. 

ii) Αν δεν ασκούμε δύναμη στον ΑΓ, η ταχύτητά του θα μειωθεί.

iii) Ο αγωγός ΔΖ θα επιταχυνθεί προς τα δεξιά.

iv) Η αρχική επιτάχυνση του ΔΖ είναι ανάλογη της ταχύτητας υ του ΑΓ.

Απάντηση:

ή

 Επαγωγή και δύο αγωγοί

 Επαγωγή και δύο αγωγοί

Ποιες οι εντάσεις των δύο αγωγών;

Δίνονται δύο ευθύγραμμοι αγωγοί (1) και (2), μεγάλου μήκους, όπου ο πρώτος είναι οριζόντιος και διαρρέεται από ρεύμα έντασης Ι₁ και ο δεύτερος είναι κατακόρυφος, διαρρεόμενος από ρεύμα έντασης Ι₂, όπως στο σχήμα.

Θέλουμε να σχεδιάσουμε την ένταση του μαγνητικού πεδίου, που δημιουργεί κάθε αγωγός, στο σημείο Α του οριζοντίου επιπέδου που βρίσκεται ο πρώτος αγωγός. Μας δίνονται τέσσερις εκδοχές:

i) Ποιο από τα παραπάνω σχήματα δείχνει σωστά τις δύο (συνιστώσες) εντάσεις, όπου Β₁ η ένταση του πεδίου που δημιουργεί ο οριζόντιος και Β₂ η ένταση του μαγνητικού πεδίου που δημιουργεί ο κατακόρυφος αγωγός;

ii) Να σχεδιάστε πάνω στο σωστό σχήμα την (συνολική) ένταση του μαγνητικού πεδίου στο σημείου Α.

iii) Αν δούμε το παραπάνω σύστημα «από πάνω» θα πάρουμε το διπλανό σχήμα. Να σχεδιάσετε τις συνιστώσες της έντασης Β₁ και Β₂ που οφείλονται στους δύο αγωγούς, στο σημείο Α.

Απάντηση:

ή

 Ποιες οι εντάσεις των δύο αγωγών;

 Ποιες οι εντάσεις των δύο αγωγών;

Δυο ισορροπίες, η μία με ράβδο

 

Ένα σώμα Σ μάζας m ηρεμεί δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, στη θέση (1) του σχήματος. Δένουμε μέσω νήματος, το σώμα Σ στο άκρο ομογενούς ράβδου μάζας Μ=2m, το άλλο άκρο της οποίας στηρίζεται σε λείο οριζόντιο επίπεδο και αφήνουμε το σύστημα να ταλαντωθεί. Εξαιτίας αποσβέσεων, μετά από λίγο το σώμα Σ ηρεμεί ξανά στη θέση (2).

i)  Στη θέση (2) το ελατήριο είναι κατακόρυφο ή όχι; Να δικαιολογήσετε την απάντησή σας.

ii) Αν U₁ η δυναμική ενέργεια του ελατηρίου στη θέση (1) και U₂ η αντίστοιχη στη θέση (2), ισχύει:

α) U₂=2U₁,   β) U₂=3U₁,   γ) U₂=4U₁,   δ) U₂=5U₁.

iii) Να αποδείξτε ότι η απώλεια της μηχανικής ενέργειας, εξαιτίας των αποσβέσεων, είναι ίση με την αρχική δυναμική ενέργεια του ελατηρίου U₁.

Απάντηση:

ή

  Δυο ισορροπίες, η μία με ράβδο

 Δυο ισορροπίες, η μία με ράβδο

Ράβδος με …. ακλόνητες απόψεις!!!

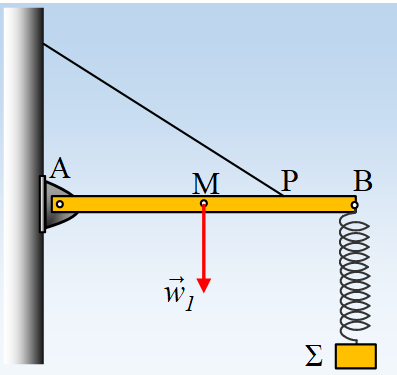
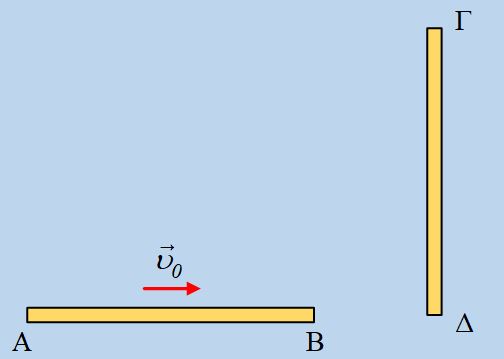
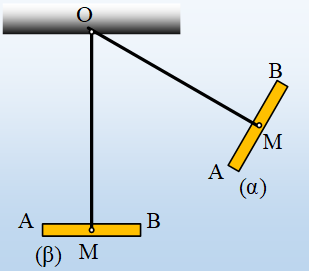
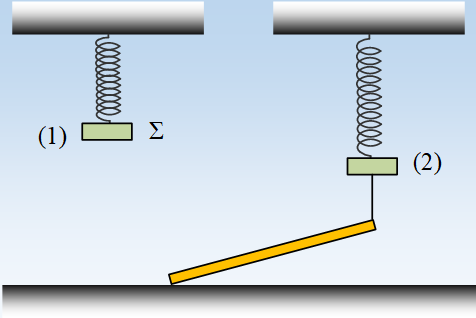
Ένα σώμα μάζας m_ολ = 0,3 kg είναι δεμένο στο ένα άκρο οριζοντίου ελατηρίου το άλλο άκρο του οποίου είναι δεμένο στο άκρο κατακόρυφης ράβδου μήκους ℓ = 2 m.  Η ράβδος είναι αναρτημένη σε σταθερό σημείο Ο (που μπορεί να κινείται γύρω από αυτό χωρίς τριβές) και ισορροπεί κατακόρυφα. Η ράβδος που έχει  αντίσταση R = 50 Ω και βάρος w = 6 N, είναι αγώγιμη και συνδεδεμένη μέσω διακόπτη με πηγή εναλλασσόμενης τάσης της μορφής υ = Vημωt. διαρρέεται από εναλλασσόμενο ρεύμα.  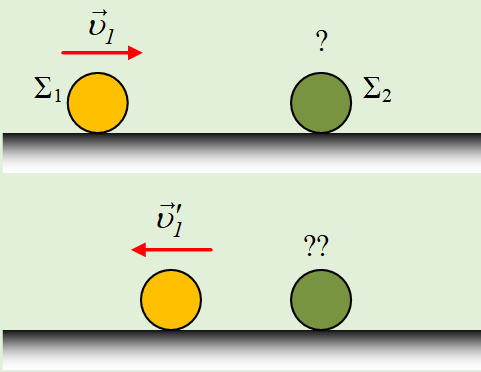Το όλο σύστημα βρίσκεται μέσα σε μαγνητικό πεδίο έντασης Β = 2 T. Μία έκρηξη προκαλεί διάσπαση του σώματος Σ σε δύο κομμάτια το οποίο ένα μένει δεμένο στο ελατήριο (το Σ₁) και κάνει οριζόντια ταλάντωση της μορφής x = 0,2ημ20t S.I. Ταυτόχρονα με την έκρηξη κλείνουμε το διακόπτη και η ράβδος διαρρέεται από εναλλασσόμενο ρεύμα. Η ενέργεια που απελευθερώθηκε από την έκρηξη είναι κατά 50% μεγαλύτερη από την ενέργεια της ταλάντωσης σώματος Σ₁.

Να βρεθούν:

α. Η σταθερά k του ελατηρίου που είναι δεμένο το Σ₁

β. Το ποσό θερμότητας που εκλύεται από την ράβδο σε μία περίοδο της ταλάντωσης του Σ₁

γ. Τα στοιχεία κανονικής λειτουργείας μιας συσκευής που συμπεριφέρεται ως ωμικός αντιστάτης αντίστασης R₁ = 5 Ω, που μπορούμε να συνδέσουμε με την παραπάνω εναλλασσόμενη τάση, ώστε να λειτουργεί κανονικά.

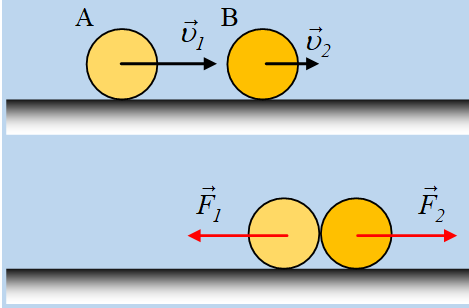
Το Σ₂ μετά την έκρηξη αφού διανύσει απόσταση d, συγκρούεται κεντρικά και ελαστικά με σώμα Σ₃ μάζας m₃ = 0,6 kg, που είναι δεμένο σε οριζόντιο ελατήριο σταθεράς k₃. Σε χρονικό διάστημα Δt₂ = 13π/30 s, μετά την έναρξη της ταλάντωσης του Σ₃ η κινητική του ενέργεια είναι τριπλάσια της δυναμικής ενέργειας της ταλάντωσης για 5^η φορά, ενώ την ίδια χρονική στιγμή το Σ₂ συγκρούεται με το Σ₁ το οποίο περνά από τη θέση ισορροπίας του κινούμενο αντίθετα σε σχέση με το Σ₂

δ. Ποια η μέγιστη δύναμη που δέχεται το Σ₃ κατά την διάρκεια της ταλάντωσης του;

ε. Πόσο διάστημα έχει διανύσει το Σ₁ από την στιγμή της έκρηξης μέχρι να συγκρουστεί με το Σ₂

στ. Ποια το μέτρο της μέγιστης δύναμης που δέχεται η ράβδος από τον άξονά της;

Δίνεται ότι το ελατήριο και τα σώματα Σ₁, Σ₂ (το δεύτερο κομμάτι από το Σ δεν είναι αγώγιμα και δεν επηρεάζονται από το μαγνητικό πεδίο. Η χρονική διάρκεια των κρούσεων θεωρείται αμελητέα

Η συνέχεια εδώ.

Η κίνηση μιας ράβδου

 

Σε λείο οριζόντιο επίπεδο κινείται ελεύθερα μια λεπτή ομογενής οριζόντια ράβδος ΑΒ και στο σχήμα δίνονται οι ταχύτητες του άκρου Α και του σημείου Μ, όπου (ΟΜ)=(ΜΒ) κάποια στιγμή t₁. Η ταχύτητα του Α έχει την διεύθυνση της ράβδου και μέτρο υ₁, ενώ η ταχύτητα υ₂ του Μ σχηματίζει γωνία θ με τη ράβδο. Το σχήμα μας δείχνει τη ράβδο σε κάτοψη.

i)  Συμφωνείτε ή διαφωνείτε με τις παρακάτω δύο προτάσεις;

α) Η κίνηση της ράβδου είναι μεταφορική.

β) Το μέσον Ο της ράβδου παραμένει ακίνητο.

ii) Ποιο από τα διανύσματα α, β, γ και δ του δεξιού σχήματος μπορεί να παριστάνει την ταχύτητα του μέσου Ο της ράβδου;

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Η κίνηση  μιας ράβδου

  Η κίνηση  μιας ράβδου

Δύο αγωγοί, ο ένας απείρου μήκους.

Στα παρακάτω σχήματα, έχουμε έναν ευθύγραμμο αγωγό (ε), πολύ μεγάλου (απείρου) μήκους, ο οποίος διαρρέεται από ρεύμα έντασης Ι και έναν ομογενή αγωγό (ΑΓ) μήκους 2α, ο οποίος διαρρέεται από ρεύμα έντασης Ι₁.

 

i)  Στο (1^ο) σχήμα, οι αγωγοί είναι παράλληλοι και η απόσταση μεταξύ τους είναι α. Από ποια εξίσωση υπολογίζεται η ασκούμενη στον ΑΓ δύναμη Laplace F₁,  από το μαγνητικό πεδίο του αγωγού (ε);

ii)  Να κατατάξετε τις ασκούμενες δυνάμεις στον αγωγό ΑΓ, κατά φθίνουσα σειρά (όσον αφορά τα μέτρα τους), δίνοντας σύντομες δικαιολογήσεις.

iii) Σε ποιες από τις παραπάνω περιπτώσεις, ο αγωγός ΑΓ, τείνει να περιστραφεί εξαιτίας της ασκούμενης δύναμης Laplace;

Απάντηση:

ή

 Δύο αγωγοί, ο ένας απείρου μήκους.

 Δύο αγωγοί, ο ένας απείρου μήκους.

Μία παράλληλη σύνδεση και η δύναμη Laplace.

  

Σε ένα κύκλωμα περιλαμβάνεται ένας βρόχος σχήματος ισοπλεύρου τριγώνου ΑΒΓ πλευράς α, όπου οι δύο κλάδοι διαρρέονται από ίσα ρεύματα Ι₁=Ι₂=Ι. Το τρίγωνο βρίσκεται μέσα σε ένα ομογενές μαγνητικό πεδίο, όπου στο επίπεδό του η ένταση Β του πεδίου, είναι κάθετη στην βάση του ΒΓ, όπως στο σχήμα.

i)  Αν F₁ το μέτρο της δύναμης που δέχεται από το πεδίο ο κλάδος ΒΑΓ και F₂ το μέτρο της αντίστοιχης δύναμης που δέχεται ο άλλος κλάδος ( η πλευρά ΒΓ), ισχύει:

 

  α) F₁ = ½ F₂,   β) F₁=F₂,  γ) F₁=2F₂

ii) Ποια θα ήταν η αντίστοιχη απάντησή σας, αν το τρίγωνο γινόταν σκαληνό με πλευρές α, β και γ, όπως στο σχήμα;

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

Μία παράλληλη σύνδεση και η δύναμη Laplace.

Μία παράλληλη σύνδεση και η δύναμη Laplace.