Μια τετράγωνη πλάκα που δεν ανατρέπεται…

 

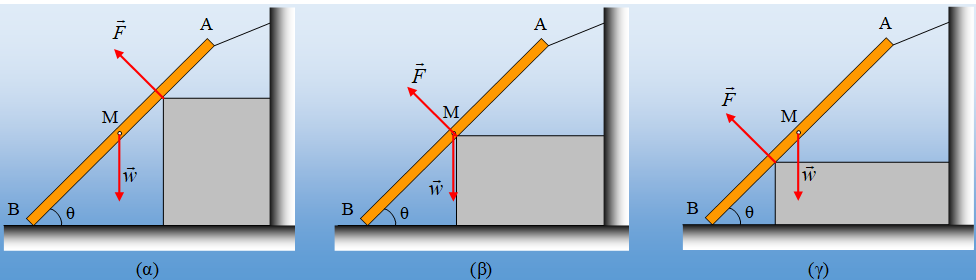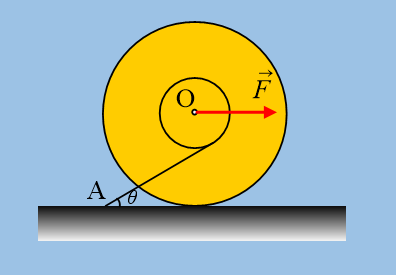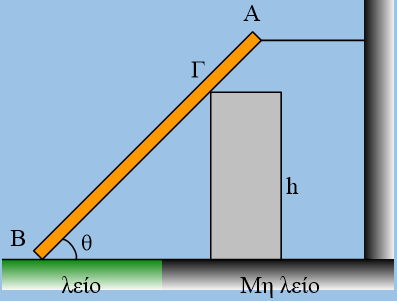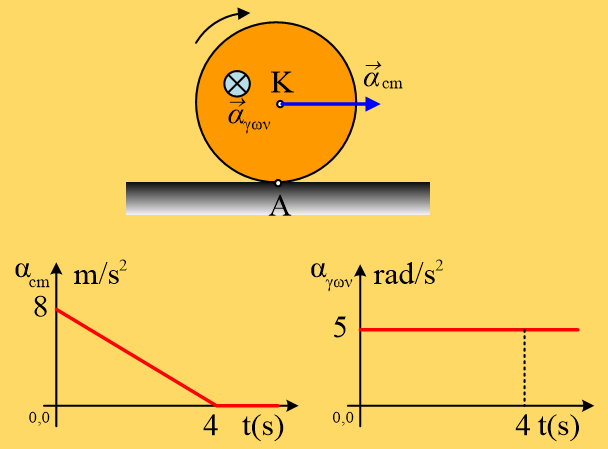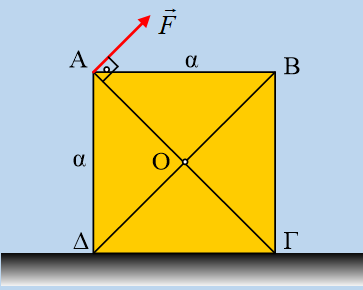
Μια ομογενής τετράγωνη πλάκα πλευράς α=1m και μάζας 50kg (w=500Ν) ηρεμεί όρθια, σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μ_s=μ=0,3. Ασκούμε στην κορυφή Α μια  δύναμη F, κάθετη στη διαγώνιο ΑΓ, όπως στο σχήμα.

i)   Αν η δύναμη F έχει μέτρο F=100Ν, να υπολογιστούν όλες οι δυνάμεις που ασκούνται στην πλάκα και να βρεθούν οι ροπές τους ως προς το κέντρο της Ο.

ii) Να βρεθεί η επιτάχυνση της κορυφής Α, αν αυξήσουμε το μέτρο της ασκούμενης δύναμης στην τιμή F₁=170Ν.

iii) Ποια είναι η μέγιστη επιτάχυνση που μπορεί να αποκτήσει το κέντρο μάζας Ο της πλάκας, χωρίς να αρχίσει η πλάκα να ανατρέπεται και για ποια τιμή της ασκούμενης δύναμης θα συμβεί αυτό;

Απάντηση:

ή

 Μια τετράγωνη πλάκα που δεν ανατρέπεται…

 Μια τετράγωνη πλάκα που δεν ανατρέπεται…

Πότε εξασφαλίζεται η ισορροπία;

Στο σχήμα μια ομογενής λεία ράβδος ΑΒ, ισορροπεί σε λείο οριζόντιο επίπεδο, σχηματίζοντας γωνία θ με αυτό, δεμένη με νήμα, στο άκρο της Α. Το νήμα σχηματίζει με την οριζόντια διεύθυνση κλίση μικρότερη από τη γωνία θ. Η ράβδος στηρίζεται σε ορθογώνιο δεχόμενη δύναμη F, ενώ παρακάτω βλέπετε τρεις εκδοχές, οι οποίες αντιστοιχούν σε διαφορετικά ύψη του ορθογωνίου και στις οποίες δεν χάνεται η επαφή με το οριζόντιο επίπεδο, στο άκρο Β.

  

Η ράβδος μπορεί να ισορροπεί:

α) Μόνο στο (α) σχήμα.

β) Στα σχήματα  (α) και (β)

γ) Σε όλα τα σχήματα

δ) Δεν μπορούμε να απαντήσουμε, αφού μας λείπουν δεδομένα.

Να δικαιολογήσετε την επιλογή σας.

Απάντηση

ή

 Πότε εξασφαλίζεται η ισορροπία;

 Πότε εξασφαλίζεται η ισορροπία;

Ένας κύλινδρος ισορροπεί

 

Στο σχήμα βλέπουμε έναν κύλινδρο βάρους w=42Ν και ακτίνας R, που στο κεντρικό του τμήμα φέρει εγκοπή ακτίνας r=0,4R, και στην οποία έχουμε τυλίξει ένα αβαρές και μη εκτατό νήμα, το άκρο του οποίου έχουμε δέσει σε σταθερό σημείο Α του εδάφους, έτσι ώστε το νήμα να σχηματίζει με το οριζόντιο επίπεδο γωνία θ όπου ημθ=0,6 και συνθ=0,8.

 είναι οριζόντιο και τεντωμένο. Ασκούμε στο κέντρο του κυλίνδρου οριζόντια δύναμη με μέτρο F=12Ν και ο κύλινδρος ισορροπεί.

i)  Να σχεδιάστε τις δυνάμεις που ασκούνται στον κύλινδρο, δικαιολογώντας την κατεύθυνσή τους, χωρίς να προβείτε σε υπολογισμούς.

ii) Να υπολογίστε το όριο θραύσης του νήματος, ώστε να εξασφαλίζεται η παραπάνω ισορροπία.

iii) Ποιος ο ελάχιστος συντελεστής οριακής στατικής τριβής μεταξύ κυλίνδρου επιπέδου, ο οποίος εξασφαλίζει την απαραίτητη δύναμη στατικής τριβής;

iv) Πόση θα ήταν η τάση του νήματος στην περίπτωση που είχαμε τυλίξει αντίθετα το νήμα στην εγκοπή, διατηρώντας την ίδια γωνία θ με το οριζόντιο επίπεδο.

Απάντηση:

ή

Ένας κύλινδρος ισορροπεί

Ένας κύλινδρος ισορροπεί

Το εμπόδιο εξασφαλίζει την ισορροπία

 

Μια ομογενής λεία ράβδος ΑΒ, μήκους ℓ=1m και βάρους w=40Ν, ισορροπεί όπως στο σχήμα, σχηματίζοντας γωνία θ με το λείο οριζόντιο επίπεδο, όπου ημθ=0,6 (συνθ=0,8), δεμένη με οριζόντιο νήμα, στο άκρο της Α. Η ράβδος στηρίζεται στην κορυφή Γ ενός βαρέος ορθογωνίου, ύψους h, το οποίο ισορροπεί σε μη λείο επίπεδο.

i)   Αν h=45,6cm, να υπολογιστεί η τάση του νήματος και η  δύναμη που ασκείται στη ράβδο από το οριζόντιο επίπεδο.

ii) Να βρεθεί το ελάχιστο ύψος h_min του ορθογωνίου, ώστε να μην χάνει η ράβδος την επαφή με το λείο οριζόντιο επίπεδο, διατηρώντας σταθερή την κλίση της θ με το επίπεδο, με δεδομένο ότι το ορθογώνιο παραμένει ακίνητο.

iii) Να βρεθεί η τριβή που ασκείται στο ορθογώνιο από το επίπεδο στην παραπάνω περίπτωση,

Απάντηση.

ή

 Το εμπόδιο εξασφαλίζει την ισορροπία

 Το εμπόδιο εξασφαλίζει την ισορροπία

Η σύνθετη κίνηση ενός τροχού

 

Ένας τροχός ακτίνας R=0,8m ηρεμεί σε οριζόντιο επίπεδο. Τη στιγμή t_ο=0 τίθεται σε κίνηση αποκτώντας επιτάχυνση κέντρου μάζας Κ, όπως στο πρώτο από τα διπλανά διαγράμματα και γωνιακή επιτάχυνση, όπως στο δεύτερο διάγραμμα.

Να βρεθούν η ταχύτητα και η οριζόντια επιτάχυνση του σημείου επαφής του τροχού με το επίπεδο, σημείου Α, τις χρονικές στιγμές:

i) t₁= 2s,   ii) t₂= 4⁺(s) και iii)  t₃= 5s.

(η στιγμή t₂=4⁺s είναι ελάχιστα μεγαλύτερη από τη στιγμή 4s, οπότε έχει μηδενιστεί η επιτάχυνση του Κ.)

Απάντηση:

ή

 Η σύνθετη κίνηση ενός τροχού

 Η σύνθετη κίνηση ενός τροχού

Ένα σύστημα αρχίζει να στρέφεται

 

Ένας ομογενής δίσκος κέντρου Κ και ακτίνας R=1m μπορεί να περιστρέφεται χωρίς τριβές γύρω από άρθρωση στο άκρο Κ μιας ράβδου (ΟΚ) μήκους l=4m, η οποία μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο, γύρω από σταθερό άξονα ο οποίος περνά από το άκρο της Ο. Το σύστημα ηρεμεί με την ράβδο κατακόρυφη. Τυλίγουμε στο δίσκο ένα αβαρές νήμα και σε μια στιγμή t=0, ασκούμε μια κατάλληλη οριζόντια δύναμη στο δίσκο, με αποτέλεσμα αμέσως μετά μόλις ασκηθεί η δύναμη F, ο δίσκος να αποκτά γωνιακή επιτάχυνση α_γων,1=5rad/s² αρχίζοντας να περιστρέφεται αριστερόστροφα, ενώ ταυτόχρονα το μέσον Μ της ράβδου αποκτά οριζόντια επιτάχυνση α_Μ=1m/s². Για τη στιγμή t=0⁺:

i)  Να σημειωθεί στο σχήμα η γωνιακή επιτάχυνση του δίσκου, για την περιστροφή του γύρω από τον άξονα στο άκρο Κ της ράβδου, καθώς και η γωνιακή επιτάχυνση για την περιστροφή της ράβδου.

ii) Να βρεθεί η επιτάχυνση του σημείου Α, στην περιφέρεια του δίσκου και στην προέκταση της ράβδου.

iii) Ποια είναι αντίστοιχα η αρχική επιτάχυνση του αντιδιαμετρικού σημείου του Α (σημείο Β);

Απάντηση.

ή

 Ένα σύστημα αρχίζει να στρέφεται

 Ένα σύστημα αρχίζει να στρέφεται

Ένας πλαγιασμένος δίσκος κινείται

 

Ένας οριζόντιος ομογενής δίσκος ακτίνας R=0,5m ηρεμεί σε λείο οριζόντιο επίπεδο, με το κέντρο του Ο στην αρχή x=0 ενός οριζόντιου άξονα x΄x, στη θέση (1). Σε μια στιγμή δέχεται ένα κατάλληλο συνδυασμό ροπής και δύναμης, με αποτέλεσμα να αποκτά μια σταθερή επιτάχυνση κέντρου μάζας και να κινείται κατά μήκος του άξονα x, ενώ ταυτόχρονα αρχίζει να περιστρέφεται με φορά αντίθετη των δεικτών του ρολογιού και στο διάγραμμα δίνεται η μεταβολή της γωνιακής του ταχύτητας, η οποία τη στιγμή t₁=2s όπου το κέντρο Ο έχει φτάσει στη θέση (2) σταθεροποιείται. Αν μόλις σταθεροποιηθεί η γωνιακή ταχύτητα μηδενίζεται η επιτάχυνση του σημείου Α (η ακτίνα ΟΑ βρίσκεται πάνω στον άξονα x), ζητούνται:

i) Η γωνιακή επιτάχυνση του δίσκου.

ii) Η επιτάχυνση του κέντρου μάζας Ο, καθώς και η απόσταση μεταξύ των θέσεων (1) και (2).

iii) Η ταχύτητα του σημείου Α τη στιγμή t=2s, καθώς και η ταχύτητα και η επιτάχυνση του σημείου Β, όπου η ακτίνα ΟΒ είναι κάθετη στην ΟΑ, τη στιγμή που μηδενίζεται η γωνιακή επιτάχυνση του δίσκου.

Απάντηση:

ή

 Ένας πλαγιασμένος δίσκος κινείται

 Ένας πλαγιασμένος δίσκος κινείται

Ξεκινώντας από τις ταχύτητες δύο σημείων

Στο σχήμα δίνονται 4 περιπτώσεις στερεών. Στις δυο πρώτες περιπτώσεις ένας ομογενής τροχός κινείται σε οριζόντιο επίπεδο, ενώ στις  δύο τελευταίες (τα σχήματα σε κάτοψη), μια ομογενής ράβδος κινείται σε οριζόντιο επίπεδο.

Στα σχήματα έχουν σχεδιαστεί οι ταχύτητες του κέντρου μάζας Ο και ενός σημείου Α, κάθε στερεού. Για καθεμία από τις 4 περιπτώσεις:

α) Να σημειώστε πάνω στο σχήμα το διάνυσμα της γωνιακής ταχύτητας περιστροφής.

β) Να σχεδιάσετε την ταχύτητα του σημείου Β.

Να δώσετε σύντομες δικαιολογήσεις.

Απάντηση:

ή

Ξεκινώντας από τις ταχύτητες δύο σημείων

Ξεκινώντας από τις ταχύτητες δύο σημείων

Η ράβδος πέφτει κατακόρυφα

 

Μια λεπτή ομογενής ράβδος ΑΒ, μήκους 4m, πέφτει κατακόρυφα και σε μια στιγμή σχηματίζει με την οριζόντια διεύθυνση γωνία θ (ημθ=0,6), ενώ το άκρο της Α έχει ταχύτητα όπως στο σχήμα, με κατεύθυνση προς το άκρο Β και μέτρου υ_Α=3m/s.

i)  Να βρεθεί η ταχύτητα του κέντρου μάζας Ο της ράβδου καθώς και η γωνιακή της ταχύτητα.

ii) Να υπολογιστεί η ταχύτητα του μέσου Μ  της ΟΒ.

Απάντηση:

ή

 Η ράβδος πέφτει κατακόρυφα

 Η ράβδος πέφτει κατακόρυφα

Οι ταχύτητες σημείων ενός δίσκου

 

Στο διπλανό σχήμα ένας δίσκος κινείται σε οριζόντιο επίπεδο με ταχύτητα του κέντρου Ο ίση με υ, ενώ ένα σημείο Μ της κατακόρυφης διαμέτρου, στο μέσον της ακτίνας, έχει επίσης ταχύτητα παράλληλη προς το έδαφος με ταχύτητα 2υ.

i) Να βρεθεί η ταχύτητα του άκρου της κατακόρυφης διαμέτρου Α.

ii) Ποιο από τα διανύσματα 1, 2, 3 και 4 παριστάνει την ταχύτητα του σημείου Β, στο άκρο μιας οριζόντιας ακτίνας ΟΒ;

iii) Η γωνία θ που σχηματίζει το διάνυσμα της ταχύτητας του σημείου Β με την οριζόντια διεύθυνση, μπορεί να έχει τιμή:

α) θ < 45°,   β) θ=45°,   γ) θ > 45°.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

 Οι ταχύτητες σημείων ενός δίσκου

 Οι ταχύτητες σημείων ενός δίσκου

Η κινηματική της περιστροφής

Μια ράβδος ΟΑ, μήκους l=4m, στρέφεται σε οριζόντιο επίπεδο, γύρω από κατακόρυφο άξονα ο οποίος περνά από το άκρο της Ο και σε μια στιγμή t=0, βρίσκεται στη θέση που δείχνει το σχήμα έχοντας γωνιακή ταχύτητα ω_ο=1rad/s.

Στο παρακάτω διάγραμμα δίνεται η γραφική παράσταση της γωνιακής ταχύτητάς της ράβδου σε συνάρτηση με το χρόνο.

i)   Να σημειωθούν πάνω στο σχήμα, για τη χρονική στιγμή t_ο=0, η γραμμική ταχύτητα, η επιτρόχιος επιτάχυνση και η κεντρομόλος επιτάχυνση του άκρου Α της ράβδου και στη συνέχεια να υπολογιστούν τα μέτρα τους.

ii) Να βρεθεί η θέση της ράβδου τη στιγμή t₁=2s και να υπολογιστεί η επιτάχυνση του άκρου Α, στη θέση αυτή.

iii) Σε ποια θέση βρίσκεται η ράβδος τη στιγμή t₂=4s; Να σχεδιαστεί ένα σχήμα που να φαίνεται η ταχύτητα του άκρου Α της ράβδου, τη στιγμή αυτή και να υπολογισθούν το μέτρο της και ο ρυθμός μεταβολής του μέτρου της.

Απάντηση.

ή

Η κινηματική της περιστροφής

Η κινηματική της περιστροφής

Αν και συγκοινωνούντα δοχεία…

 

Το κλειστό δοχείο του σχήματος περιέχει νερό σε ύψος h, πάνω από το οποίο έχει εγκλωβιστεί μια ποσότητα αέρα, ενώ πολύ κοντά στον πυθμένα του υπάρχει μια μικρή οπή που κλείνεται με τάπα. Το δοχείο έχει συνδεθεί με ανοικτό κατακόρυφο σωλήνα, στον οποίο το νερό έχει ανέβει μέχρι ύψος Η.

i)   Η πίεση του εγκλωβισμένου αέρα στο πάνω μέρος του δοχείου, έχει τιμή:

α) p₁ < p_ατμ,   β) p₁ = p_ατμ,   γ)  p₁ > p_ατμ.

όπου p_ατμ η ατμοσφαιρική πίεση, στο εξωτερικό του δοχείου.

ii) Ανοίγουμε την τάπα και αποκαθίσταται μια μόνιμη ροή. Η ταχύτητα εκροής του νερού είναι ίση:

 

Να δικαιολογήσετε τις απαντήσεις σας θεωρώντας το νερό ασυμπίεστο ιδανικό ρευστό, ενώ η βάση του δοχείου έχει πολύ μεγαλύτερο εμβαδόν από το αντίστοιχο της οπής.

Απάντηση:

ή

 Αν και συγκοινωνούντα δοχεία…

 Αν και συγκοινωνούντα δοχεία…

Υπολογίζουμε ταχύτητα ροής μετρώντας ύψος

 

Μια μεγάλη κυλινδρική δεξαμενή περιέχει νερό σε ύψος h, ενώ κοντά στον πυθμένα της έχει συνδεθεί ένας οριζόντιος σωλήνας, με αρχική διατομή Α₁=2,5cm², ο οποίος στενεύει σε τελική διατομή Α₂=1cm², όπου στο άκρο του φράσσεται με τάπα. Ένας δεύτερος κατακόρυφος σωλήνας Β, συνδέεται όπως στο σχήμα, περιέχει  νερό μέχρι ύψος h₁, ενώ κλείνεται στην κορυφή του επίσης με τάπα, έχοντας εγκλωβίσει κάποια ποσότητα αέρα.

i) Να υπολογιστεί η πίεση του εγκλωβισμένου αέρα στο κατακόρυφο σωλήνα, αν h-h₁=Δh=40cm.

ii) Ανοίγουμε ταυτόχρονα και τις δύο τάπες. Μετά την αποκατάσταση μόνιμης ροής, παρατηρούμε ότι το νερό στον κατακόρυφο σωλήνα βρίσκεται σε ύψος h₂=105cm.

α) Να υπολογιστεί η πίεση στον άξονα του οριζόντιου σωλήνα, κάτω ακριβώς από τον κατακόρυφο σωλήνα.

β) Να βρεθεί η ταχύτητα εκροής του νερού από το άκρο του οριζόντιου σωλήνα.

γ) Ποιο το ύψος h του νερού της δεξαμενής;

Δίνονται p_ατμ=10⁵Ν/m², η πυκνότητα του νερού ρ=1.000kg/m³ , g=10m/s², ενώ κατά την ροή που αποκαθίσταται δεν μεταβάλλεται πρακτικά το ύψος του νερού της δεξαμενής.

Απάντηση:

ή

 Υπολογίζουμε ταχύτητα ροής μετρώντας ύψος

 Υπολογίζουμε ταχύτητα ροής μετρώντας ύψος