Παρασκευή 16 Ιουνίου 2017
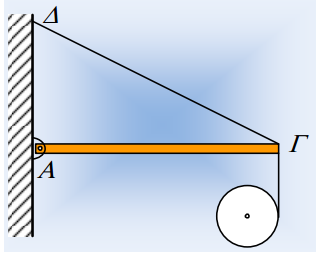
222. Σώμα πάνω σε σανίδα
Πέμπτη 15 Ιουνίου 2017
Ο κόφτης έφτασε.
Α. Αφήνουμε το σύστημα ελεύθερο να κινηθεί οπότε αρχικά επιταχύνεται ώσπου να αποκτήσει σταθερή ταχύτητα και στην συνέχεια κινείται ομαλά. Να βρείτε:
α. την αρχική επιτάχυνση (t0 = 0) της μάζας m2
Τρίτη 13 Ιουνίου 2017
Όταν ο κόφτης κάνει λάθος
 |
Δευτέρα 12 Ιουνίου 2017
Θέματα Πανελλαδικών Εξετάσεων στη Φυσική 2017
Κυριακή 4 Ιουνίου 2017
Μας έπεσε ο ουρανός στο κεφάλι.
Ένα σώμα Σ1, μάζας
m1
= 4 kg,
βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και
είναι δεμένο στο ένα άκρο
οριζόντιου ιδανικού ελατηρίου σταθεράς
k
= 200 N/m,
το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Το ελατήριο έχει αρχικά το
φυσικό του μήκος. Ασκώντας δύναμη, μετατοπίζουμε το σώμα ώστε το ελατήριο να
επιμηκύνεται, και τη χρονική στιγμή
t0
= 0 αφήνουμε ελεύθερο το σύστημα, με το ελατήριο να είναι παραμορφωμένο από το
φυσικό μήκος του κατά
d
= 0,6 m.
Σε μια επόμενη χρονική στιγμή, κατά την οποία το σώμα Σ1 διέρχεται
από μια θέση όπου το ελατήριο είναι επιμηκυμένο κατά
x1
= 0,2 m,
ένα δεύτερο σώμα Σ2, που έχει αφεθεί από ύψος
h
= 0,8 m,
μάζας m2
= 20/3 kg,
συγκρούεται πλαστικά με το σώμα Σ1, χωρίς το συσσωμάτωμα να
αναπηδήσει. Να βρείτε:
α. τα μέτρα των ταχυτήτων των σωμάτων λίγο πριν την κρούση τους
β. την απώλεια της μηχανικής ενέργειας του συστήματος των δύο σωμάτων που χάθηκε κατά την κρούση
γ. ποιο σώμα αφέθηκε πρώτο να κινηθεί
δ. σε πόση απόσταση από τη θέση όπου αφέθηκε ελεύθερο το σώμα Σ1 θα μηδενιστεί στιγμιαία η ταχύτητα του συσσωματώματος για πρώτη φορά.