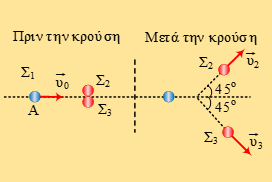
Τρεις
λείες σφαίρες Σ1, Σ2
και Σ3, μάζας m
= 1 kg
και ίδιας ακτίνας η καθεμία, βρίσκονται ακίνητες επάνω σε λεία οριζόντια
επιφάνεια, με τις σφαίρες Σ2 και Σ3 να εφάπτονται μεταξύ
τους. Κάποια χρονική στιγμή εκτοξεύουμε τη σφαίρα Σ1 με ταχύτητα υ0,
μέτρου 10√2 m/s,
προς τη θετική κατεύθυνση του άξονα
x′x,
ο οποίος διέρχεται από το σημείο επαφής των σφαιρών Σ2 και Σ3,
όπως απεικονίζεται στο παραπάνω σχήμα. Η σφαίρα Σ1 συγκρούεται
ελαστικά με τις σφαίρες Σ2 και Σ3. Μετά την κρούση οι
ταχύτητες υ2 και υ3 των σφαιρών Σ2 και Σ3
αντίστοιχα σχηματίζουν γωνία 45° η καθεμία με τον άξονα
x′x,
ενώ η Σ1 παραμένει πάνω στον άξονα
x′x.
α. Να υπολογίσετε τα μέτρα των ταχυτήτων υ2 και υ3 των σφαιρών Σ2 και Σ3 αντίστοιχα.
β. Να αποδείξετε ότι μετά την κρούση η σφαίρα Σ1 ακινητοποιείται.
Θεωρούμε ως t0 = 0 τη στιγμή της 1ης κρούσης. Την στιγμή t1 = 1 s, η σφαίρα Σ3 συγκρούεται με βλήμα μάζας m = 0,2 kg πλαστικά με αποτέλεσμα το συσσωμάτωμα να κινηθεί κάθετα στην αρχική διεύθυνση της Σ3 (παράλληλα με τη Σ2) και τη χρονική στιγμή t2 = 3 s, να φτάσει στην ελάχιστη απόσταση με τη Σ2. Να βρείτε:

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.