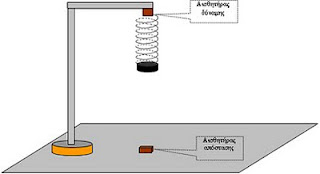
Στην διάταξη του σχήματος εικονίζεται ένα σώμα μάζας m=1Kg, το οποίο ισορροπεί κρεμασμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k=100N/m.Το άνω άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο αισθητήρα δύναμης, ο οποίος μετρά την δύναμη που ασκεί το ελατήριο σε αυτόν.
Στην ίδια κατακόρυφο με τον άξονα του ελατηρίου και σε απόσταση d=0,3m από το σώμα βρίσκεται ένας αισθητήρας απόστασης, ο οποίος μετρά την απόσταση του σώματος από αυτόν.
Οι δύο αισθητήρες είναι συνδεδεμένοι με ένα σύστημα multilog, το οποίο μπορεί να καταγράφει τις ενδείξεις των δύο αισθητήρων συναρτήσει του χρόνου.
Ανυψώνουμε το σώμα σε τέτοια θέση ώστε ο αισθητήρας δύναμης να δείχνει μηδέν.
Την στιγμή t=0 αφήνουμε το σώμα ελεύθερο να κινηθεί.
Να υπολογίσετε:
α) Την περίοδο και το πλάτος της ταλάντωσης που θα εκτελέσει το σώμα.
β) Την εξίσωση της απομάκρυνσης του σώματος από την θέση ισορροπίας του συναρτήσει του χρόνου.
γ) Την εξίσωση της απόστασης S του σώματος από τον αισθητήρα απόστασης συναρτήσει του χρόνου.
δ) Την ένδειξη F του αισθητήρα δύναμης συναρτήσει του χρόνου.
ε) Τη σχέση F=g(S) και να την παραστήσετε γραφικά.
στ) Τον χρόνο που απαιτείται μέχρι η επιμήκυνση του ελατηρίου να γίνει ίση με τα ¾ της μεγίστης τιμής της για πρώτη φορά।
Απάντηση σε pdf και σε Word
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.