Θέμα Δ #22
Ομογενής κυκλικός τροχός (Τ) ακτίνας R=1m εφάπτεται σε πλάγιο επίπεδο που σχηματίζει γωνία θ=30° με το οριζόντιο επίπεδο. Το ανώτατο σημείο του τροχού είναι δεμένο μέσω αβαρούς νήματος με μικρό σώμα (σ) μάζας m=1kg. Το σώμα (σ) εφάπτεται σε λείο οριζόντιο επίπεδο και είναι δεμένο στο ελεύθερο άκρο οριζοντίου ιδανικού ελατηρίου σταθεράς Κ=100Ν/m, το άλλο άκρο του οποίου είναι δέσμιο. Το νήμα έχει περαστεί από αβαρή τροχαλία (τ) ώστε το τμήμα που συνδέει το σώμα (σ) με την τροχαλία (τ) έχει διεύθυνση που συμπίπτει με τον άξονα του ελατηρίου ενώ το τμήμα του που συνδέει τον τροχό (Τ) με την τροχαλία (τ) είναι παράλληλο με το πλάγιο επίπεδο. Στην παρακάτω εικόνα φαίνεται κατακόρυφη επίπεδη διατομή της διάταξης, παράλληλα στην οποία γίνονται όλες οι κινήσεις. Αντίσταση αέρα δεν υπάρχει. Δίνεται g=10m/s2.
Α. Η διάταξη ισορροπεί και το ελατήριο έχει υποστεί επιμήκυνση Δℓ=0,1m. Να υπολογίσετε τη μάζα του τροχού (Τ).
Β. Τη χρονική στιγμή t0=0 κόβουμε και απομακρύνουμε το νήμα. Ο τροχός (Τ) κυλίεται χωρίς ολίσθηση ενώ το σώμα (σ) εκτελεί απλή αρμονική ταλάντωση. Τη χρονική στιγμή t1=2s το κέντρο του τροχού (Τ) έχει μετατοπιστεί κατά x1=5m. Να δείξετε ότι η μάζα του τροχού είναι συγκεντρωμένη στην περιφέρειά του.
Γ. Να υπολογίσετε το μέτρο της ταχύτητας του σώματος (σ) τη χρονική στιγμή t2= που η στροφορμή σπίν του τροχού (Τ) έχει μέτρο:


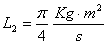
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.