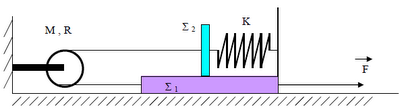
Στην παραπάνω διάταξη η σανίδα Σ 1 έχει μάζα m 1 = 21 kg και μεγάλο μήκος , το σώμα Σ 2 έχει μάζα m 2 = 8 kg και για την τροχαλία δίνονται Μ = 2 kg , I = M R 2 / 2 . Τα σώματα Σ 1 , Σ 2 είναι δεμένα μεταξύ τους με αβαρές νήμα το οποίο περνά από την περιφέρεια της τροχαλίας και το Σ 2 δεμένο στο άκρο του ιδανικού ελατηρίου σταθεράς Κ = 160 Ν / m ,του οποίου το άλλο άκρο είναι ακλόνητα δεμένο στο στέλεχος που βρίσκεται καρφωμένο στη σανίδα . Τριβές δεν υπάρχουν.
Αρχικά το σύστημα ηρεμεί με το νήμα τεντωμένο και το ελατήριο στο φυσικό του μήκος . Τη στιγμή t = 0 ασκούμε στη σανίδα την οριζόντια δύναμη που φαίνεται στο σχήμα, με μέτρο που μεταβάλλεται με την παραμόρφωση d του ελατηρίου από το φυσικό του μήκος , ώστε F = 320 d + 7,5 ( S I ) . Παρατηρούμε ότι τα σώματα κινούνται με σταθερή επιτάχυνση και το νήμα δεν ολισθαίνει στην περιφέρεια της τροχαλίας .
α) Να υπολογίσετε την επιτάχυνση των σωμάτων Σ 1 , Σ 2 .
β) Τη χρονική στιγμή που το μέτρο της δύναμης είναι 71,5 Ν , να υπολογίσετε την κινητική ενέργεια της τροχαλίας.
γ) Τη χρονική στιγμή t =√5/2 s , καταργούμε τη δύναμη , κόβουμε το νήμα και ακινητοποιούμε ακαριαία τη σανίδα . Να υπολογίσετε το πλάτος της α α τ που θα εκτελέσει το σύστημα ελατηρίου – Σ 2 .
δ) Όταν το Σ 2 βρεθεί στη μέγιστη θετική απομάκρυνση από τη θέση ισορροπίας του ( t = 0 ) , αρχίζει να επιδρά δύναμη απόσβεσης της μορφής F / = - b υ , οπότε το πλάτος της ταλάντωσης μειώνεται εκθετικά με το χρόνο . Θεωρούμε ότι η περίοδος της φθίνουσας ταλάντωσης είναι ίση με την περίοδο της ελεύθερης αμείωτης ταλάντωσης του συστήματος. Μετά από 5 πλήρεις ταλαντώσεις , το έργο της δύναμης απόσβεσης είναι – 975/128 J . Να υπολογίσετε τη σταθερά Λ της ταλάντωσης .
Απάντηση:
Απάντηση:

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.