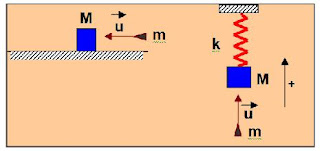
Ένα σώμα μάζας M , ηρεμεί πάνω σε οριζόντιο επίπεδο. Ένα βλήμα μάζας m , κινείται οριζόντια και συγκρούεται κεντρικά πλαστικά με το σώμα. Ο συντελεστής τριβής ολίσθησης μεταξύ συσσωματώματος και οριζόντιου επίπεδου είναι μ = 0,1 και το συνολικό διάστημα που διανύει το συσσωμάτωμα μετά την κρούση είναι S = 1,5m.
Η ίδια κρούση, πραγματοποιείται με το σώμα μάζας Μ , δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου , με το βλήμα να κινείται κατακόρυφα προς τα επάνω, κατά μήκος του άξονα του ελατηρίου.
Το πάνω άκρο του ελατηρίου, είναι ακλόνητα στερεωμένο.
Μετά την κρούση, το συσσωμάτωμα εκτελεί απλή αρμονική ταλάντωση με εξίσωση απομάκρυνσης χρόνου x = Aημ(5t+π/6) SI, θετική φορά προς τα επάνω και D = k.
Αν το κλάσμα της δυναμικής ενέργειας του ελατηρίου όταν το συσσωμάτωμα ηρεμεί στιγμιαία στην κάτω ακραία θέση της ταλάντωσής του, προς την ολική ενέργεια της ταλάντωσης, ισούται με 4 να υπολογίσετε:
1. Την ταχύτητα του συσσωματώματος αμέσως μετά την κρούση.
2. Την μέγιστη ταχύτητα του συσσωματώματος, κατά την διάρκεια της ταλάντωσης.
3. Την τιμή του λόγου m/M.
4. Την χρονική στιγμή που ξαναπερνά για πρώτη φορά το συσσωμάτωμα που ταλαντώνεται, από το σημείο που έγινε η κρούση.
5. To κλάσμα της ενέργειας του βλήματος, τη στιγμή της σύγκρουσης , που μετατράπηκε σε ενέργεια του ταλαντωτή.
Η χρονική διάρκεια των κρούσεων να θεωρηθεί αμελητέα.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.