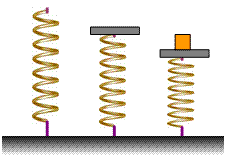
Δίσκος μάζας Μ=1kg είναι τοποθετημένος, χωρίς να είναι δεμένος, πάνω σε ελατήριο με k=100N/m, το κάτω άκρο του οποίου είναι ακλόνητο, και ισορροπεί.
Α… Πάνω στο δίσκο τοποθετούμε χωρίς ταχύτητα σώμα ίσης μάζας m=1kg, οπότε το σύστημα αρχίζει να κατέρχεται κάνοντας ΓΑΤ.
α. Μετά από πόσο χρόνο από την τοποθέτηση του σώματος το σύστημα θα φτάσει την κατώτερη θέση του;
β. Να υπολογίσετε το μέτρο της δύναμης, που δέχεται το σώμα από το δίσκο στην κατώτερη θέση.
Β… Τη στιγμή, που το σύστημα είναι στην κατώτερη θέση, αφαιρούμε το σώμα.
γ. Σε πόσο χρόνο μετά την αφαίρεση του σώματος ο δίσκος περνά από τη θέση φυσικού μήκους του ελατηρίου;
δ. πόση ταχύτητα έχει εκεί και σε πόσο μέγιστο ύψος (ως προς την κατώτερη θέση) τελικά θα φτάσει;
Δίνεται g=10m/s2.

Ίρις καλησπέρα,
ΑπάντησηΔιαγραφήενδιαφέρουσα άσκηση η οποία έχει πολλά να διδάξει.
Θα ήθελα μόνο να κάνω δύο παρατηρήσεις:
α) αντί να λες: "αντιστοιχεί στο μισό του θετικού πλάτους της ΓΑΤ" νομίζω ότι είναι προτιμότερο να πεις: " στο μισό της μέγιστης θετικής απομάκρυνσης" αφού το πλάτος είναι πάντα θετικό.
β) για λόγους καλύτερης κατανόησης του ιδανικού ελατηρίου, ίσως ήταν καλό να συμπληρώσεις:
" ο δίσκος συνεχίζει την άνοδο χωρίς να τραβήξει το ελατήριο μαζί του....το οποίο επειδή έχει αμελητέα μάζα, δεν εμφανίζει αδράνεια, οπότε παύει να κινείται"
Τα παραπάνω αποτελούν πρόταση και σε καμία περίπτωση διόρθωση.
Υ.Γ: Είδες η κρούση και η διατήρηση της ορμής τι συζήτηση μπορεί να ανοίξει!!!
Καλησπέρα Θοδωρή
ΑπάντησηΔιαγραφήΔιάβασα με ενδιαφέρον τις προτάσεις σου για βελτίωση των εκφράσεων που χρησιμοποίησα στην άσκηση και θα ήθελα να σε ευχαριστήσω γι΄αυτές. Οι επισημάνσεις από αξιόλογους συναδέλφους είναι πάντα ευπρόσδεκτες. Θα προβώ σύντομα στις αλλαγές που προτείνεις. Χαίρομαι, τέλος, που στο θέμα της κρούσης συμφωνήσαμε εξ αρχής...